Experimental purpose
Understand and master the heuristic search process of game tree, and be able to realize simple game with selected programming language.
- Learning minimax search and α − β \alpha-\beta α − β prune.
- Use the learned algorithm to realize one word chess
Experimental principle
Rules of the game
"One character chess" game (also known as "Sanzi chess" or "Jingzi chess") is a very classic puzzle game. The chessboard of "tic tac toe" is very simple. It is a 3 × The grid of 3 is very similar to the word "well" in Chinese characters, so it is named "well chess" The rules of the tic tac toe game are very similar to those of Gobang. The rule of Gobang is that one party will win when the five pieces are connected into a line first "Tic tac toe" is a game in which one side wins when three sons form a line The age of tic tac toe chess is estimated to be unknown. Westerners believe that it was invented by the ancient Romans; But we Chinese believe that since we have all invented go and Gobang, it is natural to invent a backgammon. These are purely verbal disputes, not to mention for the time being.
Minimax analysis
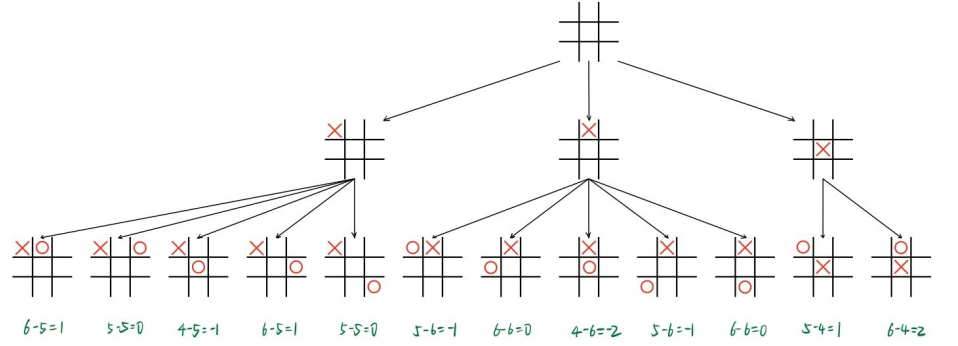
There are nine spaces. MAX and MIN play chess. Whoever takes the turn to play chess will put his own chess piece on the space. Whoever makes his chess pieces form "three pieces into a line" (the same row, column or diagonal are all someone's chess pieces) will win.
MAX is represented by a circle and MIN is represented by a cross. For example, in the following figure, MAX wins the chess game:

The valuation function is defined as follows:
Set the chess game as P P P. The valuation function is e ( P ) e(P) e(P).
- if P P P is not the winning position for either party, then $e § = e (the total number of complete rows, columns or diagonals that are still empty for MAX) - E (the total number of complete rows, columns or diagonals that are still empty for MIN)$
- if P P P is the chess game that MAX must win, then e ( P ) = + ∞ e(P)=+∞ e(P) = + ∞ (actually assigned 60)
- if P P P is the chess game that B must win, then e ( P ) = − ∞ e(P)=-∞ e(P) = − ∞ (actually assigned - 20)
such as P P P as shown below, then e ( P ) = 5 − 4 = 1 e(P)=5-4=1 e(P)=5−4=1

It should be noted that, + ∞ +∞ +∞ assignment 60 60 60, − ∞ -∞ − ∞ assignment − 20 -20 − 20 is because if the machine wins, no matter whether the player will win in the next step, he will take this step and win the chess.
α-β Pruning algorithm
The above minimax analysis method is actually a game tree, and then calculate its backward value, so that the efficiency of minimax analysis method is low. Based on the minimax analysis method α − β \alpha-\beta α − β Pruning technology.
α − β \alpha-\beta α − β The basic idea or algorithm of pruning technology is to calculate and evaluate the backward value of each node while generating the game tree, and stop expanding those unnecessary sub nodes in time according to the evaluated backward value range, that is, it is equivalent to cutting off some branches on the game tree, so as to save machine overhead and improve search efficiency.
The specific pruning methods are as follows:
- For a and node MIN, if the supremum of its backward value can be estimated β \beta β, And this β \beta β The infimum of the estimated backward value of the parent node (must be or node) whose value is not greater than MIN α \alpha α, Namely α ≥ β α≥β α ≥ β, Then there is no need to expand the other child nodes of the MIN node (because the estimation of these nodes has no impact on the back extrapolation value of the MIN parent node). This process is called α α α prune.
- For a node or MAX, if the infimum of its backstepping value can be estimated α α α, And this α α α The supremum of the estimated backward value of the parent node (must be the same as the node) whose value is not less than MAX β β β, Namely α ≥ β α≥β α ≥ β, Then there is no need to expand the other child nodes of the MAX node (because the estimation of these nodes has no impact on the back value of the MAX parent node). This process is called β β β prune.
From the algorithm:
- MAX node (including start node) α α α Value never decreases
- Of MIN node (including starting node) β β β Value never increases
During the search, α α α and β β β The values are calculated as follows:
- Of a MAX node α α α Value is equal to the current maximum final backstepping value of its successor node
- Of a MIN node β β β Value is equal to the current minimum final backstepping value of its successor node
Take an example to understand the process:
Detailed steps:
- The tree should be processed from the penultimate layer, and all processing should be "left to right"
- The value of MIN layer node is the minimum value of its child nodes. If any child nodes are cut, the minimum value of the remaining child nodes will be taken
- The value of the MAX layer node is the maximum value of its child nodes. If any child nodes are cut, the maximum value of the remaining child nodes will be taken
- Pruning can only be carried out if the following criteria are met
- Assuming that there is node x, the value range of node x is determined according to a child node of node X
- Node x also has parent nodes (including direct parent nodes and indirect parent nodes). When you determine the value of node x, these parent nodes may or may not have a value range
- If these parent nodes already have a value range, if there is no intersection between the aggregate value range of node X and the value range of the parent node (directly or indirectly) of node x, or there is only one element in the intersection, other child nodes of node x will be cut off. Other child nodes refer to all child nodes of node x except the node from which the range of node x is derived
- Pruning ends when the values of all nodes that have not been pruned are determined
Design of winning or losing judgment algorithm
Because only the currently placed pieces will win or lose each time, the winning or losing algorithm only needs to scan from the current point to judge whether three pieces have been formed. For the eight directions of this sub, judge whether it has formed three sub. If yes, it means that one party wins. If not, continue to search until one party wins or search the whole chessboard.
experimental design
Two versions are implemented, one is the C + + version and the other is the Java version.
The C + + version has poor visualization and less functions, but α − β \alpha-\beta α − β The minimax algorithm of pruning is relatively clear, which is convenient for learning and reviewing the algorithm;
The Java version wraps a visual shell on the basis of implementing the algorithm, making the whole program more product-oriented.
The following core algorithms are shared by the two versions, and the explanation of program design does not include the introduction to the C + + version.
Core algorithm
PvP:
Players and players do not need any algorithm in wartime. They only need to monitor each click on the chessboard. When one side wins or the chessboard is full (draw), the game ends.
PvE:
When the player fights with the computer, the player's position still does not need algorithm support, but only needs to be controlled by the player.
For computers, the minimax analysis method is realized by recursion to select the best placement. This algorithm not only needs to define the function of the simulation computer to find the best place, but also needs to define the function of the simulation player to find the best place, and simulate the process of taking turns by calling two functions in turn (recursion). For a certain state encountered by the computer, that is, when you want to select the placement position, recursion is carried out. After finding the best placement position, recursion is returned.
When to return recursively is the pruning condition. In this algorithm, the number of pruning layers is specified as two. When reaching the third layer, if it is impossible to lock the chess game (lock the chess game: you can determine the winner or draw), call the evaluation function for the recursive node to evaluate. One of the information returned recursively is the evaluation in this state, The valuation function is defined as: the difference between the number of the last three sub lines of the chess pieces filled with the computer side and the number of the last three sub lines of the chess pieces filled with the player side.
The function of the computer in the function of the computer drop is to find the function of the best falling place, that is, to simulate the rotation of the falling ball to get the best position.
In the function of the computer looking for the best position, first judge whether a position can be found to make the computer win directly. If such a position exists, select this position, and the valuation of this state is positive infinite, indicating that it is bound to win; If it does not exist, judge the number of pruning layers. If it reaches the number of pruning layers, directly call the valuation function to calculate the value of the state; If the number of pruning layers is not reached, try to drop in a space, that is, mark a position on the chessboard as a piece of the computer, and then call the function of the player to find the best place to drop, that is, the computer drop is completed, and it is the simulated player's turn to drop. The player will also call the computer to find the function at the best location to realize recursion, and pass back the evaluation of the child node (child state) to the upper recursive layer by reference, and update the evaluation of the current node through the evaluation of the child node. No matter whether the current node's valuation is updated or not, backtracking is required, that is, because it is a simulated drop, the state needs to be restored to the previous state after recursive return, and the drop position needs to be empty.
If you try each method every time the simulation looks for the falling position, that is, try to fall on each empty position. The recursive process is understood as a tree building process. It can be imagined that such tree building will lead to very high time complexity (in fact, although the time complexity is very high, the time-consuming is acceptable because there are at most nine squares in tic tac toe chess) α − β \alpha-\beta α − β Prune to reduce unnecessary expenses.
Every time we recurse, we need to α \alpha α Value or β \beta β Value is passed in, so that when the next layer (i.e. the opponent) selects the drop position, it can prune to reduce the drop position to be judged.
The pruning strategy of MAX node is based on the incoming β \beta β Value, this β \beta β The value is the last state of the current MAX node, that is, the maximum value of the MIN node, because it is necessary to ensure that there is an intersection between the range of the child node (MAX) and the ancestor node (MIN), that is, to ensure that the state estimation of the MAX node must be less than β \beta β, such ( − ∞ , β ] (-∞,\beta] (−∞, β] And [ α , + ∞ ) [\alpha,+∞) [ α,+ ∞) before there is intersection. If there is already disjoint, there is no need to judge the latter, that is, pruning.
The pruning strategy of the MIN node is similar to that of the MAX node and will not be repeated. In this way, not only the best location of the computer is obtained, but also the time complexity is minimized.
Pruning process
Complete state of the first three layers:
through α − β \alpha-\beta α − β State of the first three layers of pruning:
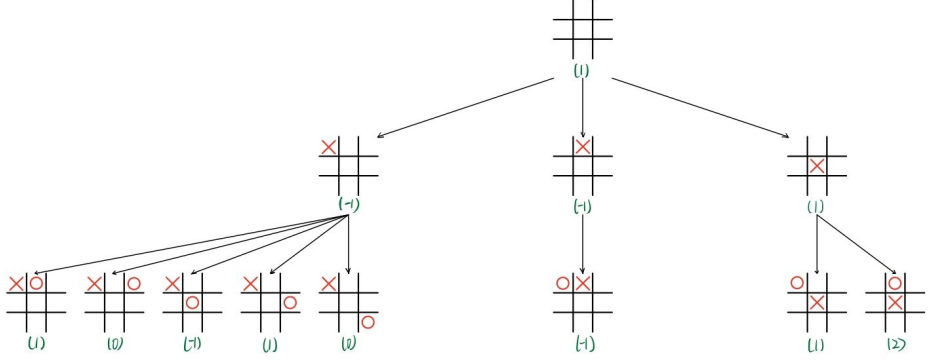
Pruning process in the program:
Pruning involves at least three layers of nodes. The implementation of pruning function is described below with three layers as an example.
The main purpose is to understand the relationship between the parameters of each layer. The top-level MAX node needs the sub node (MIN node) to transfer its parameters α \alpha α Value is used for pruning, that is, if the current MIN node β \beta β Value less than or equal to α \alpha α Pruning occurs, and there is no need to calculate the subsequent nodes in the child nodes of the MIN node; The valuation of each MAX node provided by the MIN node's child MAX node to the MIN node is not only used to update the MIN node's value β \beta β Value, also used for pruning; When the MIN node is completely updated β \beta β Value (i.e. the valuation of MIN node is determined) needs to be passed to the upper layer to update the value of MIN's parent node and MAX node α \alpha α Value.

Programming
Expected flow chart:

Flow chart of final realization:

The final implementation uses the flow shown in the second flow chart to control the whole program.
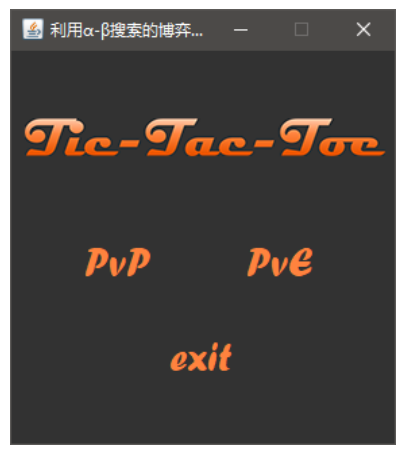
Initial interface
The initial interface consists of four parts: logo "tic tac toe", "PvP" player vs. player options, "PvE" player vs. computer options, "exit".
Game interface
The game interface mainly consists of two parts, a scoreboard at the top and a chessboard at the bottom. The scoreboard records the scores of P1 (or P) and P2 (E) respectively.
In order to easily distinguish whether the current sub square is P1 (or P) or P2 (or E), the identification of the sub square of the scoreboard is highlighted.
Rules of the game:
- When one side surpasses the other, the winner will add points, and the draw will not add points.
- In PvP mode, P1 drop is X X 10. P2 drop is O O O; In PvE mode, the computer's position is X X 10. The player's fall is O O O.
- Both parties take turns to start first and then start. P1 takes priority in PvP mode and computer takes priority in PvE mode.
PvP interface:

PvE interface:

Aspects to be optimized
-
The pop-up dialog box is transparent. In order to achieve a better user experience, when the game is over, the pop-up opaque result prompt box will block the chessboard information. When users need to observe the game, they need to drag the prompt box. Therefore, it is of great significance to make the prompt box transparent, but it can not be realized in the end.
-
The default number of pruning layers in this algorithm is 2. An error will occur when the number of pruning layers is set to 3.
-
You can also add "prompt" function in PvP mode.
Running screenshot
PvP:
The following status indicates that it is P1's turn to drop.
The following figure shows that P2 is turned to P1 after dropping the sub.

The following figure shows that P1 wins, and the pop-up prompt box shows that P1 wins.

When you click OK, the scoreboard will add one to the winner's score. At the same time, it can be seen that P1 took the lead in the last round, so P2 took the lead in this round.

PvE:
In PvE mode, the computer is given priority, and then take turns first and then.
For better user experience, the action of the computer will be delayed for 1s after calculating the optimal position of the computer, imitating the process of computer thinking.

In a draw, neither side will add points. At the same time, it will be the player's priority in the next round.


Appendix 1 (C + + code)
C + + code simply α − β \alpha-\beta α − β The minimax analysis method of pruning is realized, and the output window is used for visualization. Before writing Java code, you are familiar with the core algorithm through the C + + program.
#include<bits/stdc++.h>
using namespace std;
int chessBoard[3][3];
int isWin();
int evaluate();
bool gameOver();
void playGame();
void printChessBoard();
void computerPlace();
void humanPlace();
bool computerImmidiateWin(int&);
bool humanImmidiateWin(int&);
void findComputerBestMove(int&, int&, int, int, int);
void findHumanBestMove(int&, int&, int, int, int);
void printChessBoard() {
cout << "ChessBoard:" << endl << endl;
for(int i = 0;i < 9;i ++) {
if(chessBoard[i/3][i%3] == 1) cout << "○";
if(chessBoard[i/3][i%3] == 0) cout << "□";
if(chessBoard[i/3][i%3] == -1) cout << "×";
if(i%3 == 2) cout << endl;
}
}
int isWin() {
for(int i = 0;i < 3;i ++) {
if(chessBoard[i][0] != 0 && chessBoard[i][0] == chessBoard[i][1] && chessBoard[i][1] == chessBoard[i][2]) return chessBoard[i][0];
if(chessBoard[0][i] != 0 && chessBoard[0][i] == chessBoard[1][i] && chessBoard[1][i] == chessBoard[2][i]) return chessBoard[0][i];
}
if(chessBoard[0][0] != 0 && chessBoard[0][0] == chessBoard[1][1] && chessBoard[1][1] == chessBoard[2][2]) return chessBoard[0][0];
if(chessBoard[2][0] != 0 && chessBoard[2][0] == chessBoard[1][1] && chessBoard[1][1] == chessBoard[0][2]) return chessBoard[2][0];
return 0; // 0 does not represent a draw
}
bool computerImmidiateWin(int& bestMove) {
for(int i = 0;i < 9;i ++) {
if(chessBoard[i/3][i%3]) continue;
chessBoard[i/3][i%3] = 1;
bool win = (isWin() == 1);
chessBoard[i/3][i%3] = 0;
if(win) {
bestMove = i;
return true;
}
}
return false;
}
bool humanImmidiateWin(int& bestMove) {
for(int i = 0;i < 9;i ++) {
if(chessBoard[i/3][i%3]) continue;
chessBoard[i/3][i%3] = -1;
bool win = (isWin() == -1);
chessBoard[i/3][i%3] = 0;
if(win) {
bestMove = i;
return true;
}
}
return false;
}
int evaluate() {
int tmp[3][3], computerValue = 0, playerValue = 0;
for(int i = 0;i < 9;i ++)
tmp[i/3][i%3] = (!chessBoard[i/3][i%3]?1:chessBoard[i/3][i%3]);
for(int i = 0;i < 3;i ++)
computerValue += (tmp[i][0]+tmp[i][1]+tmp[i][2])/3 + (tmp[0][i]+tmp[1][i]+tmp[2][i])/3;
computerValue += (tmp[0][0] + tmp[1][1] + tmp[2][2])/3 + (tmp[2][0]+tmp[1][1]+tmp[0][2])/3;
for(int i = 0;i < 9;i ++)
tmp[i/3][i%3] = (!chessBoard[i/3][i%3]?-1:chessBoard[i/3][i%3]);
for(int i = 0;i < 3;i ++)
playerValue += (tmp[i][0]+tmp[i][1]+tmp[i][2])/3 + (tmp[0][i]+tmp[1][i]+tmp[2][i])/3;
playerValue += (tmp[0][0] + tmp[1][1] + tmp[2][2])/3 + (tmp[2][0]+tmp[1][1]+tmp[0][2])/3;
return computerValue + playerValue;
}
void findComputerBestMove(int& bestMove, int& value, int alpha, int beta, int deep) {
if(computerImmidiateWin(bestMove)) {
value = 60;
return ;
}
if(deep == 3) {
value = evaluate();
return ;
}
value = alpha;
for(int i = 0;i < 9 && value < beta;i ++) {
if(chessBoard[i/3][i%3]) continue;
chessBoard[i/3][i%3] = 1;
int tmp = -1, response = -1;
findHumanBestMove(tmp, response, value, beta, deep+1);
chessBoard[i/3][i%3] = 0;
if(response > value) value = response, bestMove = i;
}
}
void findHumanBestMove(int& bestMove, int& value, int alpha, int beta, int deep) {
if(humanImmidiateWin(bestMove)) {
value = -20;
return ;
}
if(deep == 3) {
value = evaluate();
return ;
}
value = beta;
for(int i = 0;i < 9 && value > alpha;i ++) {
if(chessBoard[i/3][i%3]) continue;
chessBoard[i/3][i%3] = -1;
int tmp = -1, response = -1;
findComputerBestMove(tmp, response, alpha, value, deep+1);
chessBoard[i/3][i%3] = 0;
if(response < value) value = response, bestMove = i;
}
}
void computerPlace() {
int bestMove = 0, value = 0;
const int deep = 1, alpha = -20, beta = 60;
findComputerBestMove(bestMove, value, alpha, beta, deep);
chessBoard[bestMove/3][bestMove%3] = 1;
}
void humanPlace() {
int x, y;
while(true) {
cout << "It is your turn, please input where you want :" << endl;
cout << "for example: 2 2 mean you want to add position 2 row,2 col:" << endl;
cin >> x >> y;
if (x < 0 || x > 3 || y < 0 || y > 3 || chessBoard[x-1][y-1] != 0) cout << "error, please input again:" << endl;
else break;
}
chessBoard[x-1][y-1] = -1;
}
bool gameOver() {
if(isWin()) return true;
int i;
for(i = 0;i < 9;i ++)
if(chessBoard[i/3][i%3] == 0) break;
return i == 9;
}
void playGame() {
int computerFirst;
memset(chessBoard, 0, sizeof chessBoard);
printChessBoard();
while(true) {
cout << "\nWho take the first step:\n1)Player. 2)Computer.[ ]\b\b";
cin >> computerFirst;
if(computerFirst != 1 && computerFirst != 2) getchar();
else break;
}
if(computerFirst == 2) computerPlace();
while(true) {
printChessBoard();
if(gameOver()) break;
humanPlace();
printChessBoard();
if(gameOver()) break;
computerPlace();
}
}
int main()
{
int option;
while(1) {
playGame();
if(isWin() == 0) cout << "\nDraw" << endl;
else if(isWin() == 1) cout << "\nComputer Win!\n" << endl;
else cout << "\nPlayer Win!\n" << endl;
cout << "\nTry Again?\n1)Yeah.\t2)Exit.[ ]\b\b";
cin >> option;
if(option != 1 && option != 2) getchar();
if(option == 2) break;
}
}
Appendix 2 (Java code)
The three public classes are the Main class of program entry, the Window class of interface design and the TicTacToe class of tic tac toe.
Main.java
The TicTacToe object is created. In the constructor of the TicTacToe class, the function that implements all the functions is called.
package exp2;
/**
* @author LJR
* @create 2021-11-14 21:28
*/
public class Main {
public static void main(String[] args) {
new TicTacToe();
}
}
Window.java
The interface design class also binds the click event of the button in the initial interface.
package exp2;
import javax.swing.*;
import java.awt.*;
/**
* @author LJR
* @create 2021-11-14 21:27
*/
public class Window extends JFrame {
private static final long serialVersionUID = -6740703588976621222L;
public JButton[] nineBoard = new JButton[9]; // The chessboard is full of buttons
public JButton[] buttons; // Convenient binding monitoring in tic tac toe chess class
public static boolean gameStart_PvE = false; // Does the game start
public static boolean gameStart_PvP = false; // Does the game start
public static int option = 0; // 1: PvP or 2: PvE
public JTextField[] sorceBoard_pve; // scoreboard
public JTextField[] sorceBoard_pvp;
public Window() {
super("utilizeα-βSearch the game tree algorithm to write a word chess game");
Container c = this.getContentPane();
c.add(getJButton());
c.setBackground(Color.white);
this.setSize(300, 330);
this.setUndecorated(false);
this.setLocationRelativeTo(null);
this.setVisible(true);
this.setResizable(false);
this.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
public JTextField[] generateSorceBoard(int PorE) { // Generate scoreboard
String text[][] = new String[][]{{"P1", "0", ":", "0", "P2"}, {"P", "0", ":", "0", "E"}}; // string 0 : PvP string 1 : pve
int bound_x[] = {65, 95, 125, 155, 185};
int align[] = {JTextField.LEFT, JTextField.RIGHT, JTextField.CENTER, JTextField.LEFT, JTextField.RIGHT};
int size_w = 30, size_h = 30, font_size = 20, font_flag = Font.PLAIN;
String font_style = "Forte";
JTextField[] jfs = new JTextField[5];
for (int i = 0; i < 5; i++) {
jfs[i] = new JTextField(text[PorE][i]);
jfs[i].setBounds(bound_x[i], 0, size_w, size_h);
jfs[i].setFont(new Font(font_style, font_flag, font_size));
jfs[i].setHorizontalAlignment(align[i]);
jfs[i].setForeground(new Color(255, 255, 255));
jfs[i].setOpaque(false);
jfs[i].setFocusable(false);
jfs[i].setCursor(Cursor.getPredefinedCursor(Cursor.DEFAULT_CURSOR));
jfs[i].setBorder(BorderFactory.createEmptyBorder(0, 0, 0, 0)); // Set borderless
}
return jfs;
}
public JButton[] generateButtons() { // Generate {"PvP", "PvE", "exit"} buttons
String[] text = new String[]{"PvP", "PvE", "exit"};
int[][] pos = new int[][]{{40, 140}, {160, 140}, {110, 210}}, size = new int[][]{{76, 35}, {76, 35}, {60, 35}};
JButton[] jbs = new JButton[3];
int font_size = 30, font_flag = Font.PLAIN, color_R = 255, color_G = 131, color_B = 62;
String font_style = "Forte";
for (int i = 0; i < 3; i++) {
jbs[i] = new JButton(text[i]);
jbs[i].setBounds(pos[i][0], pos[i][1], size[i][0], size[i][1]);
jbs[i].setFont(new Font(font_style, font_flag, font_size));
jbs[i].setForeground(new Color(color_R, color_G, color_B));
jbs[i].setCursor(Cursor.getPredefinedCursor(Cursor.HAND_CURSOR)); // Mouse move in button smaller hand
jbs[i].setOpaque(false); // transparent
jbs[i].setBorder(BorderFactory.createEmptyBorder(0, 0, 0, 0));
jbs[i].setContentAreaFilled(false);
jbs[i].setFocusPainted(false);
jbs[i].setRolloverEnabled(true);
}
return jbs;
}
public JPanel getJButton() {
JPanel jP = new JPanel();
jP.setOpaque(false);
jP.setLayout(null);// Set an empty layout, that is, an absolute layout
// Game interface
JPanel chessboard_panel = new JPanel();
chessboard_panel.setLayout(null);
chessboard_panel.setBounds(0, 0, 300, 330);
chessboard_panel.setBackground(new Color(45, 45, 45));
JLabel jl = new JLabel();
Icon icon1 = new ImageIcon("src/board_2.jpg"); // Attention path
jl.setIcon(icon1);
jl.setBorder(BorderFactory.createEmptyBorder(0, 0, 0, 0));
jl.setBounds(0, 30, icon1.getIconWidth(), icon1.getIconHeight());
chessboard_panel.add(jl);
chessboard_panel.setVisible(false);
jP.add(chessboard_panel);
// scoreboard
sorceBoard_pvp = generateSorceBoard(0);
sorceBoard_pve = generateSorceBoard(1);
// Start interface
JPanel start_panel = new JPanel();
start_panel.setLayout(null); // The panel must be set to an empty layout
start_panel.setBackground(new Color(50, 50, 50));
start_panel.setBounds(0, 0, 300, 330);
jP.add(start_panel);
// logo
JLabel logo = new JLabel();
Icon icon = new ImageIcon("src/TicTacToe_1.png"); // Attention path
logo.setIcon(icon);
logo.setBounds(10, 50, icon.getIconWidth(), icon.getIconHeight());
start_panel.add(logo);
buttons = generateButtons();
for (int i = 0; i < 3; i++) start_panel.add(buttons[i]);
buttons[0].addActionListener((actionEvent -> { // pvp / / bind and click listen
option = 1; // pvp
for (int i = 0; i < 5; i++) chessboard_panel.add(sorceBoard_pvp[i]);
chessboard_panel.setVisible(true);
start_panel.setVisible(false);
startGame_PvP(); // PvP start
}));
buttons[1].addActionListener((actionEvent -> { // pve
option = 2; // pve
for (int i = 0; i < 5; i++) chessboard_panel.add(sorceBoard_pve[i]);
chessboard_panel.setVisible(true);
start_panel.setVisible(false);
startGame_PvE(); // The game begins
}));
buttons[2].addActionListener((actionEvent -> { // exit
System.exit(0);
}));
// Each grid is a button
for (int i = 0; i < 9; i++) {
nineBoard[i] = new JButton();
nineBoard[i].setBounds(i % 3 * 72 + 37, i / 3 * 72 + 27, 65, 65);
nineBoard[i].setCursor(Cursor.getPredefinedCursor(Cursor.HAND_CURSOR)); // Mouse move in button smaller hand
nineBoard[i].setOpaque(false); // Transparent, with or without?
nineBoard[i].setBorder(BorderFactory.createEmptyBorder(0, 0, 0, 0)); // Temporary notes
nineBoard[i].setContentAreaFilled(false);
nineBoard[i].setFocusPainted(false);
nineBoard[i].setRolloverEnabled(true);
jl.add(nineBoard[i]);
}
return jP;
}
public void startGame_PvE() {
// System.out.println("PvE");
Window.gameStart_PvE = true; // Only when the user clicks PvE can the content in the process be executed
}
public void startGame_PvP() {
// System.out.println("PvP");
Window.gameStart_PvP = true;
}
}
TicTacToe.java
Core class, which contains various internal classes and threads. This class implements α − β \alpha-\beta α − β Pruning minimax analysis algorithm, while monitoring some of the game interface drop click and other events.
package exp2;
import javax.swing.*;
import java.awt.*;
/**
* @author LJR
* @create 2021-11-15 15:50
*/
public class TicTacToe {
Window window; // Use members from
// lock
public Object lock = new Object();
// checkerboard
int chessBoard[][] = new int[3][3];
// Variable, PvE
boolean thread_computer_over = false; // Does the computer thread end
boolean thread_human_over = false; // Does the player thread end
boolean newgame = true; // Start a new game
int cnt = 0; // Parity controls whether youCanClick is true or false. I don't know why it is invalid to object to the assignment of youCanClick
int nowStatus = 0; // Is it PvE or PvP now
int beclickedButton = -1; // The number of the clicked button
boolean humanPlaceOver = false; // Are you waiting for the player to click and drop
boolean youCanClick = false; // Controls whether the player clicks on the grid effectively, that is, if false, the player cannot fall
boolean buttonsAlive[] = new boolean[9]; // Whether the button can be clicked and whether it is valid, that is, if false, it has been dropped
// It can be seen that if you are allowed to drop a child somewhere, you must first ensure that youCanClick=true and buttonsAlive[i]=true
// Variable, PvP
boolean thread_p1_over = false; // Does the thread of player1 end
boolean thread_p2_over = false;
boolean inP1Turn = true; // Round at P1
boolean P1PlaceOver = false;
boolean P2PlaceOver = false;
// thread
ControlScoreBoardColor thread_color = new ControlScoreBoardColor();
// PvE
Computer thread_computer;
Human thread_human;
JudgeOver thread_judge = new JudgeOver();
JudgeOption thread_option = new JudgeOption();
ChangeRound thread_changeRound = new ChangeRound();
// PvP
Player1 thread_p1 = new Player1();
Player2 thread_p2 = new Player2();
JudgeOver_PvP thread_gameover_pvp = new JudgeOver_PvP();
ChangeRound_PvP thread_changeRound_pvp = new ChangeRound_PvP();
// Constructor, the entrance to everything
public TicTacToe() {
for (int i = 0; i < 9; i++) chessBoard[i / 3][i % 3] = 0; // Initialize chessboard
for (int i = 0; i < 9; i++) buttonsAlive[i] = true; // Drop is allowed at any position initially
window = new Window(); // Interface design
thread_option.start(); // Determine whether the PvP or PvE clicked by the user
addButtonClickListener();
}
// Internal class, user-defined Integer class. Because the value of the Integer class of Java is final, you must use object to realize functions similar to C + + reference
class MyInteger {
private int value;
public MyInteger() {
}
public MyInteger(int value) {
this.value = value;
}
public void setValue(int value) {
this.value = value;
}
public int getValue() {
return value;
}
}
// Internal class, a thread that changes the color of the scoreboard of the current chess player, so that the chess player can know more clearly who should fall
class ControlScoreBoardColor extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(30);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (Window.gameStart_PvP) {
if (inP1Turn) {
window.sorceBoard_pvp[0].setForeground(new Color(255, 131, 62));
window.sorceBoard_pvp[4].setForeground(new Color(255, 255, 255));
} else {
window.sorceBoard_pvp[0].setForeground(new Color(255, 255, 255));
window.sorceBoard_pvp[4].setForeground(new Color(255, 131, 62));
}
}
if (Window.gameStart_PvE) {
if (youCanClick) {
window.sorceBoard_pve[0].setForeground(new Color(255, 131, 62));
window.sorceBoard_pve[4].setForeground(new Color(255, 255, 255));
} else {
window.sorceBoard_pve[0].setForeground(new Color(255, 255, 255));
window.sorceBoard_pve[4].setForeground(new Color(255, 131, 62));
}
}
}
}
}
// Internal class, top-level thread. In this thread, different threads are started according to whether the user clicks PvP or PvE
class JudgeOption extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(100);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (Window.option == 1) {
nowStatus = 1;
Window.option = 0;
gameStart_PvP();
}
if (Window.option == 2) {
nowStatus = 2;
Window.option = 0;
gameStart_PvE();
}
}
}
}
// Internal class, PvE: the thread that determines the end of the game
class JudgeOver extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(500);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (thread_computer_over && thread_human_over) {
if (isWin() == 0) {
// Several spaces to center text
JOptionPane.showMessageDialog(null, " it ends in a draw", "Council results", 1);
// System.out.println("draw");
} else if (isWin() == 1) {
JOptionPane.showMessageDialog(null, " You failed", "Council results", 1);
window.sorceBoard_pve[3].setText(Integer.parseInt(window.sorceBoard_pve[3].getText()) + 1 + ""); // Computer integral plus one
// System.out.println("computer win");
} else {
JOptionPane.showMessageDialog(null, " You won", "Council results", 1);
window.sorceBoard_pve[1].setText(Integer.parseInt(window.sorceBoard_pve[1].getText()) + 1 + ""); // Player points plus one
// System.out.println("player win");
}
try {
Thread.sleep(300);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
clearChessBoard(); // Clear the chessboard and initialize some variables to facilitate the beginning of the next game
}
}
}
}
// Internal class, PvE: realize that the computer and players take turns first and then
class ChangeRound extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(300);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (newgame) {
newgame = false;
youCanClick = (cnt % 2 != 0);
cnt++;
thread_computer = new Computer();
thread_human = new Human();
thread_computer.setName("computer");
thread_human.setName("human");
thread_computer.start();
thread_human.start();
}
}
}
}
// Internal class, PvE: computer thread
class Computer extends Thread {
public void run() {
while (true) {
if (gameOver()) {
Window.gameStart_PvE = false; // game over
thread_computer_over = true;
// System.out.println("computer gameOver");
return;
}
try { // Not without a little sleep
Thread.sleep(50); // This sleep event can be understood as the refresh time
} catch (InterruptedException e) {
e.printStackTrace();
}
if (Window.gameStart_PvE) {
synchronized (lock) {
if (!youCanClick) { // Computer round
try { // Let the computer sleep more and imitate the tic tac toe game (if the computer is displayed directly after the player falls, the effect is not good)
Thread.sleep(1000);
} catch (InterruptedException e) {
e.printStackTrace();
}
computerPlace(); // Core algorithm
youCanClick = true;
} else {
try {
lock.wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
}
}
}
// Internal class, PvE: player thread
class Human extends Thread {
public void run() {
while (true) {
if (gameOver()) {
Window.gameStart_PvE = false; // game over
thread_human_over = true;
// System.out.println("player gameOver");
return;
}
try { // Not without a little sleep
Thread.sleep(50);
} catch (InterruptedException e) {
e.printStackTrace();
}
if (Window.gameStart_PvE) {
synchronized (lock) {
if (youCanClick) { // Player turns and
humanPlace(); // Wait for the click event to occur
youCanClick = false;
} else {
lock.notify();
}
}
}
}
}
}
// Internal class, PvP: judge whether the game is over
class JudgeOver_PvP extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(500);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (thread_p1_over && thread_p2_over) {
if (isWin() == 0) {
// Several spaces to center text
JOptionPane.showMessageDialog(null, " it ends in a draw", "Council results", 1);
System.out.println("draw");
} else if (isWin() == 1) {
JOptionPane.showMessageDialog(null, " P1 Won", "Council results", 1);
window.sorceBoard_pvp[1].setText(Integer.parseInt(window.sorceBoard_pvp[1].getText()) + 1 + ""); // P1 integral plus one
System.out.println("P1 win");
} else {
JOptionPane.showMessageDialog(null, " P2 Won", "Council results", 1);
window.sorceBoard_pvp[3].setText(Integer.parseInt(window.sorceBoard_pvp[3].getText()) + 1 + ""); // P2 integral plus one
System.out.println("P2 win");
}
try {
Thread.sleep(300);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
clearChessBoard(); // Clear the chessboard and initialize some variables to facilitate the beginning of the next game
}
}
}
}
// Internal class, PvP: Player 1 and player 2 take turns first and then hand
class ChangeRound_PvP extends Thread {
public void run() {
while (true) {
try {
Thread.sleep(300);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (newgame) {
newgame = false;
inP1Turn = (cnt % 2 == 0);
cnt++;
System.out.println(inP1Turn);
thread_p1 = new Player1();
thread_p2 = new Player2();
thread_p1.setName("P1");
thread_p2.setName("P2");
thread_p1.start();
thread_p2.start();
}
}
}
}
// Internal class, PvP: Player 1 thread
class Player1 extends Thread {
public void run() {
while (true) {
if (gameOver()) {
Window.gameStart_PvP = false; // game over
thread_p1_over = true;
// System.out.println("p1 gameOver");
return;
}
try {
Thread.sleep(50);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (Window.gameStart_PvP) {
synchronized (lock) {
if (inP1Turn) { // Round of P1
P1Place(); // P1 drop
inP1Turn = false;
} else {
try {
lock.wait();
} catch (InterruptedException exception) {
exception.printStackTrace();
}
}
}
}
}
}
}
// Internal class, PvP: Player 2 thread
class Player2 extends Thread {
public void run() {
while (true) {
if (gameOver()) {
Window.gameStart_PvP = false; // game over
thread_p2_over = true;
// System.out.println("p2 gameOver");
return;
}
try {
Thread.sleep(50);
} catch (InterruptedException exception) {
exception.printStackTrace();
}
if (Window.gameStart_PvP) {
synchronized (lock) {
if (!inP1Turn) { // Round of P2
P2Place(); // P2 drop
inP1Turn = true;
} else {
lock.notify();
}
}
}
}
}
}
// PvE: a top-level function that starts three threads: 1 Thread 2 to judge whether the Bureau ends Thread to change the color of the current player's scoreboard 3 Switch first hand thread
public void gameStart_PvE() {
thread_judge.start(); // Always alive
thread_color.start(); // Whose scoreboard is displayed in orange
thread_changeRound.setName("round");
thread_changeRound.start(); // The computer chess playing thread and the player chess playing thread are opened in this thread
}
// PvP: a top-level function that starts three threads: 1 Thread 2 to judge whether the Bureau ends Thread to change the color of the current player's scoreboard 3 Switch first hand thread
public void gameStart_PvP() {
thread_gameover_pvp.start(); // Always alive
thread_color.start();
thread_changeRound_pvp.setName("round");
thread_changeRound_pvp.start(); // The computer chess playing thread and the player chess playing thread are opened in this thread
}
// Player 1 drop function
public void P1Place() {
if (!Window.gameStart_PvP) return; // So that the player thread can terminate
// System.out.println("waiting for P1");
while (!P1PlaceOver) {
try { // Not without a little sleep
Thread.sleep(50);
} catch (Exception e) {
}
}
chessBoard[beclickedButton / 3][beclickedButton % 3] = 1;
// System.out.println("P1 place!");
P1PlaceOver = false;
}
// Player 2 drop function
public void P2Place() {
if (!Window.gameStart_PvP) return; // So that the player thread can terminate
// System.out.println("waiting for P2");
while (!P2PlaceOver) {
try { // Not without a little sleep
Thread.sleep(50);
} catch (Exception e) {
}
}
chessBoard[beclickedButton / 3][beclickedButton % 3] = -1;
// System.out.println("P2 place!");
P2PlaceOver = false;
}
// Bind click events for tic tac toe buttons. Since only lambda expressions or constants can be used in listening, you need to bind and listen to each button separately
public void addButtonClickListener() {
window.nineBoard[0].addActionListener((actionEvent -> { // 0
if (youCanClick && nowStatus == 2 && buttonsAlive[0]) { // Allow players to click
// System.out.println("effective click 0");
buttonsAlive[0] = false; // Chess pieces already exist in this position (both sides can't play again)
youCanClick = false; // Players can't drop, so the click event has happened, indicating that the player has just finished
beclickedButton = 0; // No. 0 was clicked
humanPlaceOver = true; // Used to control waiting players
window.nineBoard[0].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[0]) { // PvP
// System.out.println("effective click 0");
buttonsAlive[0] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 0; // No. 0 was clicked
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[0].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[0].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[1].addActionListener((actionEvent -> { // 1
if (youCanClick && nowStatus == 2 && buttonsAlive[1]) { // Allow players to click
// System.out.println("effective click 1");
buttonsAlive[1] = false;
youCanClick = false;
beclickedButton = 1;
humanPlaceOver = true;
window.nineBoard[1].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[1]) { // PvP
// System.out.println("effective click 1");
buttonsAlive[1] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 1;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[1].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[1].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[2].addActionListener((actionEvent -> { // 2
if (youCanClick && nowStatus == 2 && buttonsAlive[2]) { // Allow players to click
// System.out.println("effective click 2");
buttonsAlive[2] = false;
youCanClick = false;
beclickedButton = 2;
humanPlaceOver = true;
window.nineBoard[2].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[2]) { // PvP
// System.out.println("effective click 2");
buttonsAlive[2] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 2;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[2].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[2].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[3].addActionListener((actionEvent -> { // 3
if (youCanClick && nowStatus == 2 && buttonsAlive[3]) { // Allow players to click
// System.out.println("effective click 3");
buttonsAlive[3] = false;
youCanClick = false;
beclickedButton = 3;
humanPlaceOver = true;
window.nineBoard[3].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[3]) { // PvP
// System.out.println("effective click 3");
buttonsAlive[3] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 3;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[3].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[3].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[4].addActionListener((actionEvent -> { // 4
if (youCanClick && nowStatus == 2 && buttonsAlive[4]) { // Allow players to click
// System.out.println("effective click 4");
buttonsAlive[4] = false;
youCanClick = false;
beclickedButton = 4;
humanPlaceOver = true;
window.nineBoard[4].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[4]) { // PvP
// System.out.println("effective click 4");
buttonsAlive[4] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 4;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[4].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[4].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[5].addActionListener((actionEvent -> { // 5
if (youCanClick && nowStatus == 2 && buttonsAlive[5]) { // Allow players to click
// System.out.println("effective click 5");
buttonsAlive[5] = false;
youCanClick = false;
beclickedButton = 5;
humanPlaceOver = true;
window.nineBoard[5].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[5]) { // PvP
// System.out.println("effective click 5");
buttonsAlive[5] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 5;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[5].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[5].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[6].addActionListener((actionEvent -> { // 6
if (youCanClick && nowStatus == 2 && buttonsAlive[6]) { // Allow players to click
// System.out.println("effective click 6");
buttonsAlive[6] = false;
youCanClick = false;
beclickedButton = 6;
humanPlaceOver = true;
window.nineBoard[6].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[6]) { // PvP
// System.out.println("effective click 6");
buttonsAlive[6] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 6;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[6].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[6].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[7].addActionListener((actionEvent -> { // 7
if (youCanClick && nowStatus == 2 && buttonsAlive[7]) { // Allow players to click
// System.out.println("effective click 7");
buttonsAlive[7] = false;
youCanClick = false;
beclickedButton = 7;
humanPlaceOver = true;
window.nineBoard[7].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[7]) { // PvP
// System.out.println("effective click 7");
buttonsAlive[7] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 7;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[7].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[7].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
window.nineBoard[8].addActionListener((actionEvent -> { // 8
if (youCanClick && nowStatus == 2 && buttonsAlive[8]) { // Allow players to click
// System.out.println("effective click 8");
buttonsAlive[8] = false;
youCanClick = false;
beclickedButton = 8;
humanPlaceOver = true;
window.nineBoard[8].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button to indicate the drop
}
if (nowStatus == 1 && buttonsAlive[8]) { // PvP
// System.out.println("effective click 8");
buttonsAlive[8] = false; // Chess pieces already exist in this position (both sides can't play again)
beclickedButton = 8;
if (inP1Turn) {
P1PlaceOver = true; // If P1 is currently dropped, P1 is finished
window.nineBoard[8].setIcon(new ImageIcon("src/X_1.gif")); // Click to modify the background of the button, indicating P1 drop
} else {
P2PlaceOver = true; // If P2 is currently dropped, P2 is finished
window.nineBoard[8].setIcon(new ImageIcon("src/O_1.gif")); // Click to modify the background of the button, indicating P2 drop
}
}
}));
}
// Clear chessboard and initialize variables
public void clearChessBoard() {
for (int i = 0; i < 9; i++) {
chessBoard[i / 3][i % 3] = 0; // Initialize chessboard
buttonsAlive[i] = true; // The buttons are clickable
window.nineBoard[i].setIcon(new ImageIcon("src/tm.png"));
}
// PvE
thread_human_over = false;
thread_human_over = false;
Window.gameStart_PvE = true; // The game begins
newgame = true;
beclickedButton = -1; // The number of the clicked button
humanPlaceOver = false; // Are you waiting for the player to click and drop
// PvP
thread_p1_over = false;
thread_p2_over = false;
Window.gameStart_PvP = true; // The game begins
beclickedButton = -1; // The number of the clicked button
P1PlaceOver = false;
P2PlaceOver = false;
}
// ---------------Minimax algorithm core (start)---------------
// Judge whether there is a victory
int isWin() { // Judge whether there is a victory
for (int i = 0; i < 3; i++) {
if (chessBoard[i][0] != 0 && chessBoard[i][0] == chessBoard[i][1] && chessBoard[i][1] == chessBoard[i][2])
return chessBoard[i][0];
if (chessBoard[0][i] != 0 && chessBoard[0][i] == chessBoard[1][i] && chessBoard[1][i] == chessBoard[2][i])
return chessBoard[0][i];
}
if (chessBoard[0][0] != 0 && chessBoard[0][0] == chessBoard[1][1] && chessBoard[1][1] == chessBoard[2][2])
return chessBoard[0][0];
if (chessBoard[2][0] != 0 && chessBoard[2][0] == chessBoard[1][1] && chessBoard[1][1] == chessBoard[0][2])
return chessBoard[2][0];
return 0; // 0 does not represent a draw
}
// Determine whether the game is over
public boolean gameOver() {
if (isWin() != 0) return true;
int i;
for (i = 0; i < 9; i++)
if (chessBoard[i / 3][i % 3] == 0) break;
return i == 9;
}
// Calculate valuation
int evaluate() {
int tmp[][] = new int[3][3], computerValue = 0, playerValue = 0;
// Calculate the valuation of MAX (computer)
for (int i = 0; i < 9; i++)
tmp[i / 3][i % 3] = (chessBoard[i / 3][i % 3] == 0 ? 1 : chessBoard[i / 3][i % 3]);
for (int i = 0; i < 3; i++)
computerValue += (tmp[i][0] + tmp[i][1] + tmp[i][2]) / 3 + (tmp[0][i] + tmp[1][i] + tmp[2][i]) / 3;
computerValue += (tmp[0][0] + tmp[1][1] + tmp[2][2]) / 3 + (tmp[2][0] + tmp[1][1] + tmp[0][2]) / 3;
// Calculate the valuation of MIN (player)
for (int i = 0; i < 9; i++)
tmp[i / 3][i % 3] = (chessBoard[i / 3][i % 3] == 0 ? -1 : chessBoard[i / 3][i % 3]);
for (int i = 0; i < 3; i++)
playerValue += (tmp[i][0] + tmp[i][1] + tmp[i][2]) / 3 + (tmp[0][i] + tmp[1][i] + tmp[2][i]) / 3;
playerValue += (tmp[0][0] + tmp[1][1] + tmp[2][2]) / 3 + (tmp[2][0] + tmp[1][1] + tmp[0][2]) / 3;
return computerValue + playerValue;
}
// Computer: try to find the best step. If this step can win, go to the next step. Otherwise, find the best position through the minimax algorithm of alpha beta pruning
public boolean computerImmidiateWin(MyInteger bestMove) {
for (int i = 0; i < 9; i++) {
if (chessBoard[i / 3][i % 3] != 0) continue;
chessBoard[i / 3][i % 3] = 1;
boolean win = (isWin() == 1);
chessBoard[i / 3][i % 3] = 0;
if (win) {
bestMove.setValue(i); // If you find a step that can make the computer win, bestMove is set to this step and returned through "reference"
return true;
}
}
return false;
}
// Player: try to find the best step. If this step can win, go to the next step. Otherwise, find the best position through the minimax algorithm of alpha beta pruning
public boolean humanImmidiateWin(MyInteger bestMove) {
for (int i = 0; i < 9; i++) {
if (chessBoard[i / 3][i % 3] != 0) continue;
chessBoard[i / 3][i % 3] = -1;
boolean win = (isWin() == -1);
chessBoard[i / 3][i % 3] = 0;
if (win) {
bestMove.setValue(i);
return true;
}
}
return false;
}
// Computer: alpha beta pruning minimax algorithm
public void findComputerBestMove(MyInteger bestMove, MyInteger value, int alpha, int beta, int deep) {
if (computerImmidiateWin(bestMove)) { // If there is a winning step, take it
value.setValue(60); // The valuation of pizza hut is 60
return;
}
if (deep == 3) { // Up to the third layer, it is actually two layers of pruning
value.setValue(evaluate()); // Valuation of current node
return;
}
value.setValue(alpha);
for (int i = 0; i < 9 && value.getValue() < beta; i++) { // If the value of the current node (this value represents the range of the MAX node [value, + ∞) > = the beta of its ancestor node (that is, the range (- ∞, beta) of the MIN node near the tree root)
if (chessBoard[i / 3][i % 3] != 0) continue; // Non zero
chessBoard[i / 3][i % 3] = 1;
MyInteger tmp = new MyInteger(-1), response = new MyInteger(-1);
findHumanBestMove(tmp, response, value.getValue(), beta, deep + 1); // -1 is a temporary value, which will be updated in recursion; response is the evaluation of the child node and returns the value; The value value of the current node is used as the alpha value, that is, the range of the MAX node [value, + ∞), for pruning within the function
chessBoard[i / 3][i % 3] = 0; // to flash back
if (response.getValue() > value.getValue()) { // The current node is a MAX node, so it needs to be updated with the maximum value of the child node
value.setValue(response.getValue());
bestMove.setValue(i); // Update the best drop point
}
}
}
// Player: alpha beta pruning minimax algorithm
public void findHumanBestMove(MyInteger bestMove, MyInteger value, int alpha, int beta, int deep) {
if (humanImmidiateWin(bestMove)) {
value.setValue(-20);
return;
}
if (deep == 3) {
value.setValue(evaluate());
return;
}
value.setValue(beta);
for (int i = 0; i < 9 && value.getValue() > alpha; i++) {
if (chessBoard[i / 3][i % 3] != 0) continue;
chessBoard[i / 3][i % 3] = -1;
MyInteger tmp = new MyInteger(-1), response = new MyInteger(-1);
findComputerBestMove(tmp, response, alpha, value.getValue(), deep + 1);
chessBoard[i / 3][i % 3] = 0;
if (response.getValue() < value.getValue()) {
value.setValue(response.getValue());
bestMove.setValue(i);
}
}
}
// Computer drop
public void computerPlace() {
MyInteger bestMove = new MyInteger(0), value = new MyInteger(0); // Through object passing, you can achieve the effect of reference similar to C + +
final int deep = 1, alpha = -20, beta = 60;
findComputerBestMove(bestMove, value, alpha, beta, deep);
chessBoard[bestMove.getValue() / 3][bestMove.getValue() % 3] = 1;
buttonsAlive[bestMove.getValue()] = false;
// System.out.println(bestMove.getValue());
window.nineBoard[bestMove.getValue()].setIcon(new ImageIcon("src/X_1.gif"));
}
// Player drop
public void humanPlace() {
if (!Window.gameStart_PvE) return; // So that the player thread can terminate
// System.out.println("waiting for human");
while (!humanPlaceOver) {
try { // Not without a little sleep
Thread.sleep(50);
} catch (Exception e) {
}
}
chessBoard[beclickedButton / 3][beclickedButton % 3] = -1;
// System.out.println("human place!");
humanPlaceOver = false;
}
// ---------------Minimax algorithm core (end)---------------
}