Original link: http://tecdat.cn/?p=17526
Original source: Tuo end data tribal official account
This paper presents an algorithm, which can switch between mean regression and trend following strategy according to market volatility. Two models are studied: one uses historical volatility and the other uses Garch (1,1) volatility prediction. The mean regression strategy uses RSI (2) for modeling: it is Long when RSI (2), otherwise it is Short. The trend tracking strategy is cross modeled with SMA 50/200: Long when SMA (50) > SMA (200), otherwise Short.
The following code loads historical prices from Yahoo Finance and compares the effects of buy and hold, mean regression and trend tracking strategies:
#*****************************************************************
#Load historical data
#******************************************************************
load.packages('quantmod')
tickers = 'SPY'
data <- new.env()
getSymbols(tickers, src = 'yahoo', from = '1970-01-01', env = data, auto.assign = T)
#*****************************************************************
#Code strategy
#******************************************************************
prices = d
#Purchase and hold
data$weight\[
#Mean regression (MR) strategy
rsi2 = bt.apply.ma
#Trend tracking (TF) strategy
sma.short = apply.matrix(prices, SMA, 50)
sma.long = apply.matrix(prices, SMA, 200)
data$weight\[\] = NA
#*****************************************************************
#Create report
#******************************************************************
plotb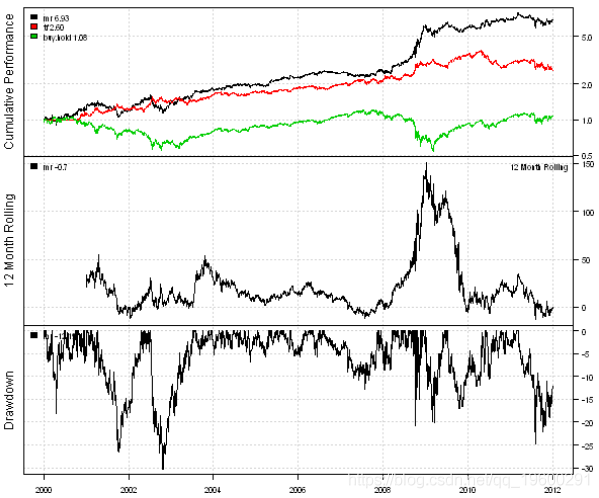
Next, let's create a strategy that switches between mean regression and trend following strategies based on historical market volatility.
#***************************************************************** #Regional system transfer according to historical market fluctuations #Current volatility is classified as a percentage using a 252 day backtracking period #****************************************************************** #District system transfer history data$weight\[\] = NA data$weight\[\] = iif(vol.rank > 0.5, iif(rsi2 < l=capital, trade.summary=T) #***************************************************************** #Create report #****************************************************************** report(regime, mr)
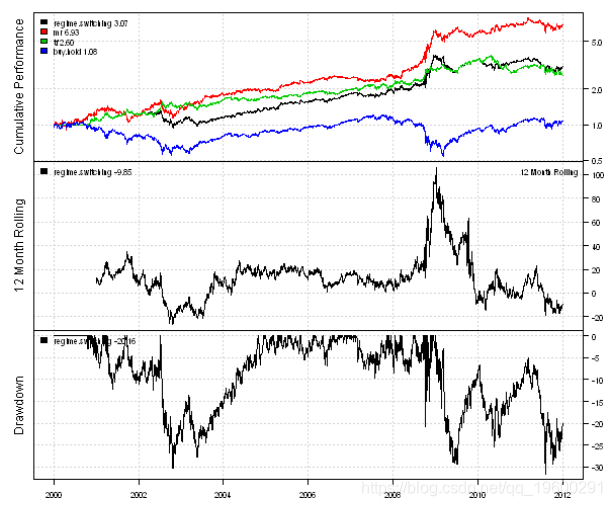
Next, we create a GARCH (1,1) volatility forecast.
There are some R packages that can fit the GARCH model. I will consider the GARCH function in the tseries package and the garchFit function in the fGarch package. The GARCH function in the tseries package is fast, but it does not always find a solution. The garchFit function in the fGarch package is slower, but converges more consistently. To demonstrate the speed difference between the GARCH function and the garchFit function, I created a simple benchmark:
#*****************************************************************
#Benchmarking Garch algorithm
#******************************************************************
temp = garchSim(n=252)
test1 <- function() {
fit1=garch(temp, order = c(1, 1), control = garch.control(trace = F))
}
test2 <- function() {
fit2=garchFit(~ garch(1,1), data = temp, include.mean=FALSE, trace=F)
}
benchmark(
test1(),
test2(),
columns=
)The garchFit function is on average 6 times slower than the garch function. Therefore, to predict volatility, I will try to use the garch function when finding a solution, otherwise I will try to use the garchFit function.
#*****************************************************************
#Using Garch to forecast volatility
#garch from tseries is fast, but it does not always converge
#The garchFit speed of fGarch is slow, but the convergence is consistent
#******************************************************************
load.packages('tseries,fGarch')
# Sigma\[t\]^2 = w + a* Sigma\[t-1\]^2 + b*r\[t-1\]^2
garch.predict.one.day <- function(fit, r1) {
hl = tail( fitted(fit)\[,1\] ,1)
#Same as forecast (fit, n.ahead=1, doplot=F)\[3 \]
garchFit.predict.one.day <- funct
garch.vol = NA * hist.vol
for( i in (252+1):nperiods
err ) FALSE, warning=function( warn ) FALSE )
if( !is.logical( fit
garch(1,1), data = temp, include.mean=FALSE, trace=F),
error=function( err ) FALSE, warning=function( warn ) FALSE )
if( !is.logical(Now, let's create a strategy that switches between mean regression and trend tracking strategies based on GARCH (1,1) volatility prediction.
#***************************************************************** #District transfer using Garch #****************************************************************** vol.rank = percent.rank(SMA(percent.rank(garch.v #District transfer Garch data$weight\[\] = NA data$weight\[\] = iif(vol.rank > 0.5, iif(rsi2 < 50, 1, -1), iif(sma.short > sma.l #***************************************************************** #Create report #****************************************************************** report(regime.switching)
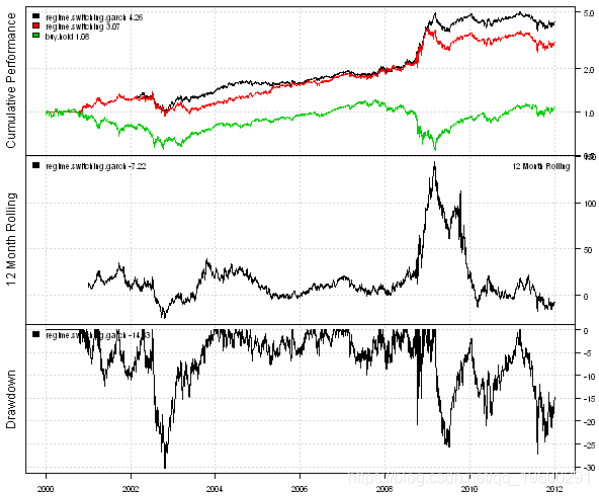
The conversion strategy using GARCH (1,1) volatility prediction is slightly better than that using historical volatility.
You can incorporate forecasts into models and trading strategies in a number of different ways. R has a very rich set of software packages for modeling and predicting time series.

Most popular insights
2.HAR-RV model based on mixed data sampling (MIDAS) regression in R language to predict GDP growth Regressive HAR-RV model predicts GDP growth ")
3.Realization of Volatility: ARCH model and HAR-RV model
5.VaR comparison of GARCH (1,1), MA and historical simulation method
6.R language multivariate COPULA GARCH model time series prediction
7.VAR fitting and prediction based on ARMA-GARCH process in R language
8.matlab predicts ARMA-GARCH conditional mean and variance model
9.ARIMA + GARCH trading strategy for S & P500 stock index in R language
