Pre question fragment

There are 13 days left for the final exam, but I still have problems in the computer room.
In fact, I didn't really want to be decadent, but this question is very important for learning to expand Europe, so I'd better put it in.

Topic introduction

Valley portal

Title Description

Crete is famous for its savage communities. There are \ (m \) caves arranged in a circle on the island. These caves are numbered clockwise \ (1,2, \ dots, m \). There are \ (n \) savages living on the island. At first, they lived in caves \ (c_1, c_2, \ dots, c_n \) in turn. After that, every year, the \ (I \) savage will walk clockwise and live in the \ (P_i \) cave.

Each savage \ (I \) has a life value \ (L_i \), that is, the number of years of survival.

The following four pictures describe the first four years on an island with \ (6 \) caves and three savages. The initial cave numbers of the three savages are \ (1,2,3 \); The number of caves to go through each year is \ (3,7,2 \); The life values are \ (4,3,1 \).

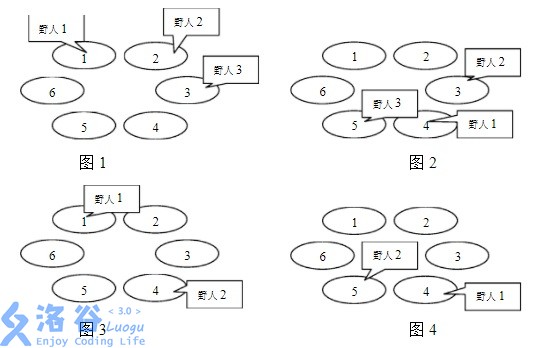
It is strange that although there are many savages, no two savages are in the same cave in their lifetime, which makes the island keep peace and tranquility, which surprises scientists. They want to know, at least how many caves can maintain peace on the island?

Input format

The \ (1 \) line is an integer \ (n(1\leq n\leq 15) \), that is, the number of savages.

From line \ (2 \) to line \ (N+1 \), each line contains three integers \ (C_i, P_i, L_i (1\leq C_i,P_i \leq 100, 0\leq L_i\leq 10^6) \), indicating the initial cave number of each savage, the number of caves traveled each year and the life value.

Output format

Contains only one number \ (m \), which is the least possible number of caves. The input data is guaranteed to have a solution, and \ (m \) is not greater than \ (10 ^ 6 \).

Problem solving process

Here is a description of the whole process.
Assuming that two savages \ (i,j \) will come together after \ (x \) years, their positions are
\((C_i+xP_i) \mod m \) and \ ((C_j+xP_j) \mod m \)
That is, there is a number \ (x \leq (min(L_i,L_j)) \) that satisfies

Then, our goal is to find the value of \ (m \) that makes these \ (n^2 \) congruence equations have no solution.
It is observed that the data range is very small and the range of \ (m \) is known. Consider the value of violent enumeration \ (m \) and solve it with extended Europe.
The code is as follows:

#include <cstdio>
#include <cctype>
#include <iostream>
#include <cmath>
using namespace std;

const int maxn = 20;
int n, m, c[maxn], p[maxn], l[maxn];

inline int read() {
	
	int x = 0, f = 1;
	char ch = getchar();
	
	while(!isdigit(ch)) {
		if(ch == '-') f = -1;
		ch = getchar(); 
	}
	
	while(isdigit(ch)) {
		x = x * 10 + ch - '0';
		ch = getchar();
	}
	
	return x * f;
}

inline int exgcd(int a, int b, int &x, int &y) {
	
	if(b == 0) {
		
		x = 1, y = 0;
		return a;
	}
	
	int r = exgcd(b, a % b, x, y), tp = x;
	x = y, y = tp - a / b * y;
	
	return r;
}

inline bool solve(int m) {
	
	for(int i = 1; i <= n; i++)
		for(int j = i + 1; j <= n; j++) {
			
			int a = p[i] - p[j], b = m, x, y;
			int gcd = exgcd(a, b, x, y), len = c[j] - c[i];
			
			if(len % gcd != 0) continue;
			a /= gcd, b /= gcd, len /= gcd;
			b = abs(b);
			x = (x * len % b + b) % b;
			if(x <= l[i] && x <= l[j]) return false;//The equation has a solution, indicating that m is not satisfactory
		}
			
	return true;
}
int main() {
	
	#ifndef ONLINE_JUDGE
	freopen("savage.in", "r", stdin);
	freopen("savage.out", "w", stdout);
	#endif
	
	n = read();
	for(int i = 1; i <= n; i++) {
		c[i] = read(), p[i] = read(), l[i] = read();
		m = max(m, c[i]);//Ensure that m is greater than or equal to any c[i]
	}
	
	while(!solve(m)) m++;
	
	printf("%d", m);
	
	return 0;
}

Post question gossip

In 20 years, this question was still purple, and in 21 years, it became blue
Although this question is very water