Hello everyone, I'm hehaige. I focus on the back end. If I can, I want to be a code designer instead of an ordinary coder to witness the growth of hehaige. Your comments, praise and attention are my biggest motivation. If there are mistakes, please don't hesitate to give me advice. Thank you very much. Let's support the original! If there is a clerical error in pure hand typing, please forgive me.

1-1: Title Description

Given an array of positive integers nums and a positive integer target, return the minimal length of a contiguous subarray [numsl, numsl+1, ..., numsr-1, numsr] of which the sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example 1:

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

Example 2:

Input: target = 4, nums = [1,4,4]
Output: 1

Example 3:

Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

Constraints:

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

Follow up: If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).

Source: LeetCode
Link: https://leetcode-cn.com/problems/minimum-size-subarray-sum
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

Topic understanding:
Find the smallest array in the middle of an array, and its sum = target.

1-2: sliding window solution

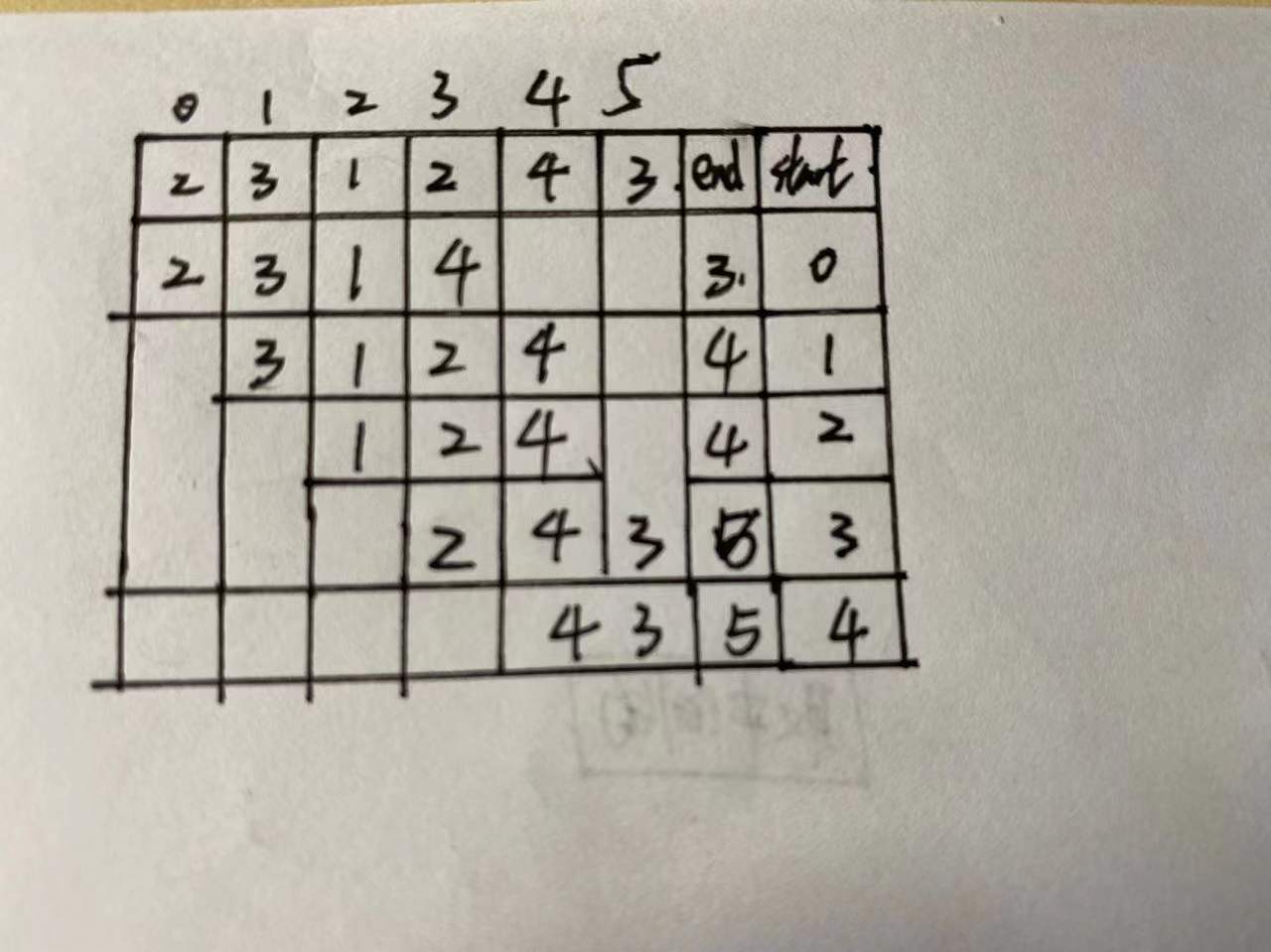
☘️ Algorithm flow:
The core idea is to use a scalable sliding window to control the size of the subarray. The whole window is left closed and right closed, [start, end]. Every time this range type topic, you must first think about where your range is? Section opening and closing? Start controls the head of the window and end controls the tail of the window. Each start pushes one to the front, representing that the window is moving. End controls the total size of the values of the window. Once the sum in the window exceeds the target, end ends. The length of the array is end - start + 1.

☘️ The overall thinking is not difficult. The difficulty lies in mastering the boundary. I don't have the ability to write it in one step. I can only try it many times through debug.

public static int minSubArrayLen(int target, int[] nums) {
    int n = nums.length;
    int minLength = Integer.MAX_VALUE;
    int start = 0;
    int end = -1;
    int sum = 0;
    while (start < n) {
        while (sum < target && end != n - 1) {
            end++;
            sum += nums[end];
        }
        if (sum >= target) {
            minLength = Math.min(minLength, end - start + 1);
        }
        sum -= nums[start];
        start++;
    }
    return minLength == Integer.MAX_VALUE ? 0 : minLength;
}

Time complexity O(N)
Spatial complexity O(1)

☘️ The idea of the answer seems different from mine. It is to maintain a sum and add numbers to the sum through end every time. When the target is reached, start to thin the window and make it just less than the target. As long as a few more numbers can meet and be greater than the target. I don't understand. You can see the figure of the official solution. In fact, it is similar to the above. The code is as follows:

public static int minSubArrayLen2(int target, int[] nums) {
    int n = nums.length;
    if (n == 0) {
        return 0;
    }
    int minLength = Integer.MAX_VALUE;
    int start = 0;
    int end = 0;
    int sum = 0;
    while (end < n) {
        sum += nums[end];
        while (sum >= target) {
            minLength = Math.min(minLength, end - start + 1);
            sum -= nums[start];
            start++;
        }
        end++;
    }
    return minLength == Integer.MAX_VALUE ? 0 : minLength;
}
Time complexity O(N)
Spatial complexity O(1)

1-3: prefix and + binary search

☘️ There is a difference between my here and the answer. What is my prefix and here? Prefix [i] = sum of num [0: I], left closed interval, right closed interval. For example, prefix [1] = num [0] + num [1];

☘️ We first give the schematic diagram under general conditions:

☘️ Since the values in the num array are integers, the prefix array must be incremented. In this way, you can find the required bound and what kind of bound meets the requirements. Write it above. Therefore, the whole algorithm has the following steps:

• Fill prefix and array
• Starting from the prefix and the first position 0, binary search the qualified bound, and calculate the length of the array interval to update.

public static int minSubArrayLen3(int target, int[] nums) {
    int n = nums.length;
    if (n == 0) {
        return 0;
    }
    int minLength = Integer.MAX_VALUE;
    int[] prefix = new int[n]; // Prefix [i]: sum of nums [0: I]
    int sum = 0;
    // fill prefix[]
    for (int i = 0; i < n; i++) {
        sum += nums[i];
        prefix[i] = sum;
    }
    for (int i = 0; i < n; i++) {
        int val = (i == 0 ? target : target + prefix[i - 1]);
        int bound = Arrays.binarySearch(prefix, val); // bound = -insertion point - 1
        // can't find the val
        if (bound < 0) {
            bound = -bound - 1;
        }
        // if find the val, the scope of bound is from 0 to n-1. [0:n-1]
        if (bound <= n - 1) {
            minLength = Math.min(minLength, bound - i + 1);
        }
    }
    return minLength == Integer.MAX_VALUE ? 0 : minLength;
}
Time complexity O(nlogn)
Spatial complexity O(n)

☘️ Pay special attention to the binary search of java. If you find the index of the return target, if you can't find it, return - the index of the insertion location - 1. Why? For example, at 0, no - 1 is not a minus sign, seconds! So < 0 is not found. Then calculate the required bound, where the "index of the inserted position" is the value of the prefix and > target. You can debug and you'll know what I'm talking about. For example:

int[] nums = new int[]{2, 3, 1, 2, 4, 3};
int target = 7;