Note: some drawing parameters come from network resources

1._ 88 merge two ordered arrays

Label: merge sort, three pointers

Idea: set three pointers to point to the tail i1 of the actual array, the array i2 and the tail i3 of the overall array.

Compare the values pointed to by i1 and i2 every time. If i2 > i1, exchange the value pointed to by i2 with the value pointed to by i3, and i2--,i3 --

If I2 < = i1, the value pointed to by i1 is exchanged with the value pointed to by i3, and i1--,i3 --

Termination condition: the pointer pointed by i2 is reduced to 0

Note: 1 Know under what conditions can sorting be terminated?

When i2 decreases to 0, the sorting ends. When i1 is reduced to 0, it indicates that array 1 has been sorted, and the value of array 2 can be directly assigned to the whole array.

              2. In what direction do you start sorting?

Start sorting from the right and the original elements will not be overwritten.

Code:

 public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i1 = m - 1;
        int i2 = n - 1;
        int i3 = m + n - 1;
        while(i2 >= 0){
            if(i1 >= 0 && nums2[i2] < nums1[i1]){
                nums1[i3--] = nums1[i1--]  ;
            }else{
                nums1[i3--] = nums2[i2--] ;
            }
        }
    }

2._ 75 color classification

 

Label: array, three pointers

Idea: note that the topic requires only one scan algorithm in constant space. That is, the space complexity is O(1) and the time complexity is O(n). Although the problem seems to be sorting, with these conditions, the sorting algorithms we have learned do not meet the conditions and are excluded.

It can be solved with three pointers. The three pointers point to the leftmost (left pointer), rightmost (right pointer) of the array, and traverse the entire array from the leftmost (traverse pointer i).

First, judge the value 0 pointed by the traversal pointer i. if it is 0, the value pointed by i and the value pointed by left are exchanged, i++,left + +,

If it is 1, i++,left does not move.

If it is 2, the value pointed to by i is exchanged with the value pointed to by right, and the value of right--,i remains unchanged

Termination condition: i > right (left points to the sorted ones on the left and right points to the sorted ones on the right)

                        

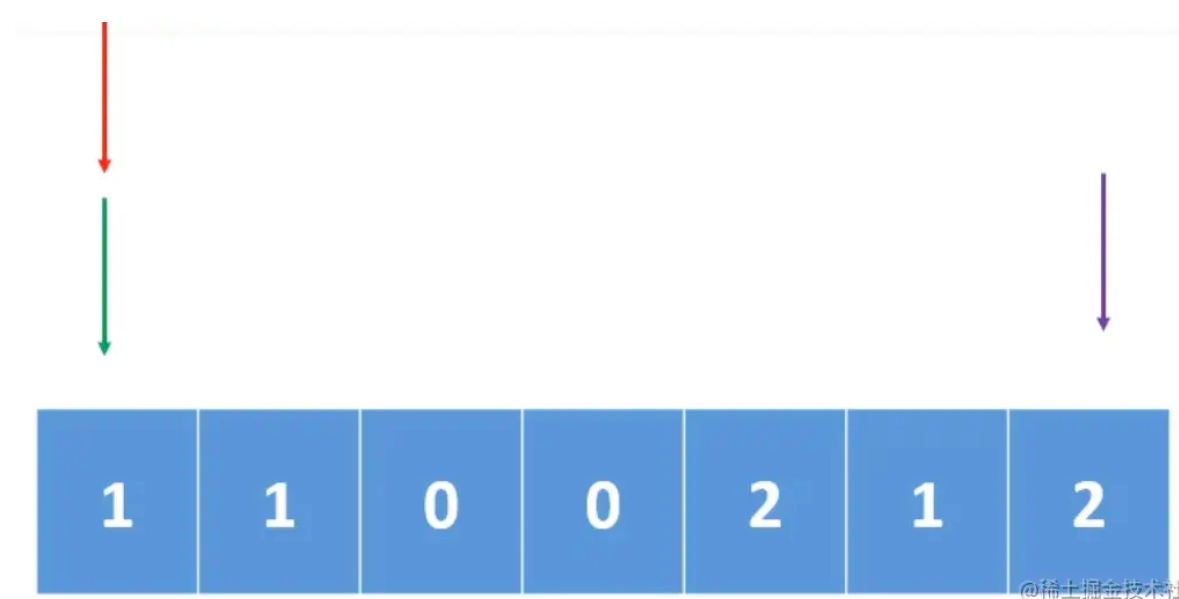
Note: 1 Termination conditions

               2. First think about how to change the pointer at each step

code:

   public void sortColors(int[] nums) {
        int left = 0,i = 0;
        int right = nums.length - 1;
        while(i <= right){
            if(nums[i] == 0){
                swap(nums,i++,left++);

            }else if(nums[i] == 1){
                i++;
            }else{
                swap(nums,i,right--);
            }
        }
    }
    private void swap(int[] nums,int i,int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

3._ 16 part sorting

Label: array, double pointer

Idea: first of all, we should understand the meaning of the question. What needs to be sorted is the reverse pair. We only need to find the reverse pair positions on the leftmost and rightmost.

• Find the reverse order pairs from left to right and from right to left respectively, so as to determine the range.
• Scan from left to right and record the maximum value. If the current value is found to be less than the maximum value, record its position (it may be in reverse order to the maximum range). If the current value is greater than the maximum value, overwrite the maximum value.
• Scan from right to left and record the minimum value. If the current value is found to be greater than the minimum value, record its position (it may be the maximum range of reverse order pair). If the current value is less than the minimum value, overwrite the minimum value.
• The position range of the two scanning records is the range to be sorted.

Note: 1 Do you need to record in case of equality?

code:

   public int[] subSort(int[] array) {
        
        if(array.length == 0) return new int[]{-1,-1};
        int max = array[0];
        int min = array[array.length - 1];
        int leftIndex = -1,rightIndex = -1; //Initializing the value of the variable to - 1 can avoid subsequent judgment
        
        for(int i = 1;i < array.length;i++){
            //From left to right, the positive order is bigger and bigger, and the reverse order is smaller and smaller. You need to find the rightmost reverse order pair
           if(array[i]  >= max){
               max = array[i];
           }else{
               rightIndex = i;
           }
        }
        //Early end
        if(rightIndex == -1) return new int[]{-1,-1};
        
        for(int i =array.length - 2;i >=0 ;i--){
            //From right to left, the positive sequence is getting smaller and smaller, and the reverse sequence is getting larger and larger. You need to find the leftmost reverse sequence pair
            if(array[i] <= min){
                min = array[i];
            }else{
                leftIndex = i;
            }
        }
        return new int[]{leftIndex,rightIndex};

    }