Classification method based on probability theory: Naive Bayes

Advantages: it is still effective in the case of less data (but the accuracy is also inexhaustible), and can deal with multi category problems.
Disadvantages: it is sensitive to the way data is input.
Applicable data type: nominal data.

Pre knowledge: conditional probability, Bayesian decision theory, independent of each other

Mutual independence: mutual independence is to let A and B be two events if the equation is satisfied P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B), then events A and B are independent of each other, abbreviated as A and B are independent.

Conditional probability: P ( g r e y ∣ b u c k e t B ) P(grey|bucketB) P(grey ∣ bucket B) represents the probability that the ball is gray when the ball is taken from bucket B.

Conditional probability calculation method
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)​
Bayesian criterion:

By substituting the conditional probability formula, the P ( A ∣ B ) P(A|B) P(A ∣ B) and P ( B ∣ A ) P(B|A) Conversion method between P(B ∣ A):
p ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) p(A|B)=\frac{P(B|A)P(A)}{P(B)} p(A∣B)=P(B)P(B∣A)P(A)​
Bayesian decision theory:

Core idea: choose the decision with the highest probability

• If p 1 ( x , y ) > p 2 ( x , y ) p1(x,y)>p2(x,y) P1 (x,y) > P2 (x,y), then (x,y) belongs to class 1

• If p 1 ( x , y ) < p 2 ( x , y ) p1(x,y)<p2(x,y) P1 (x,y) < P2 (x,y), then (x,y) belongs to class 2

Based on the above, the final Bayesian classification criteria:

• If p ( c 1 ∣ x , y ) > p ( c 2 ∣ x , y ) p(c_1|x,y)>p(c_2|x,y) p(c1 ∣ x,y) > P (C2 ∣ x,y), then (x,y) belongs to class 1
• If p ( c 1 ∣ x , y ) < p ( c 2 ∣ x , y ) p(c_1|x,y)<p(c_2|x,y) p(c1 ∣ x,y) < p (C2 ∣ x,y), then (x,y) belongs to class 2

Number of samples:

In classification, the number of features determines the number of samples. According to statistics, if N samples are required for each feature, M samples are required N M N^M NM samples, which are exponentially exploded.

If the features are independent of each other, the number of samples required can be from N M N^M NM drops to N ∗ M N*M N∗M.

Document classification using naive Bayes:

This method takes words as features, and the number of features is huge.

”Simplicity ":

The distribution of words actually affects each other, some specific grammar and some fixed collocations. This method classifies documents on the premise that the features are independent of each other, so it is simple and the purpose is to use fewer samples.

• Preparing data: building word vectors from text

• Training algorithm: calculate the probability from the word vector

According to Bayesian classification criteria, we need to obtain P ( c 0 ∣ w ) P(c_0|w) P(c0 ∣ w) and P ( c 1 ∣ w ) P(c_1|w) P(c1 ∣ w), where W is a word vector composed of multiple words (features).

Firstly, from Bayesian criterion to:
P ( c 0 ∣ w ) = P ( w ∣ c 0 ) P ( C 0 ) P ( w ) P(c_0|w)=\frac{P(w|c_0)P(C_0)}{P(w)} P(c0​∣w)=P(w)P(w∣c0​)P(C0​)​
Secondly, it is assumed by "simplicity"
P ( w ∣ c 0 ) = P ( w 1 , w 2 , ... , w n ∣ c 0 ) = P ( w 1 ∣ c 0 ) P ( w 2 ∣ c 0 ) ... P ( w n ∣ c 0 ) P(w|c_0)=P(w_1,w_2,\dots,w_n|c_0)=P(w_1|c_0)P(w_2|c_0)\dots P(w_n|c_0) P(w∣c0​)=P(w1​,w2​,...,wn​∣c0​)=P(w1​∣c0​)P(w2​∣c0​)...P(wn​∣c0​)
You can get the following pseudo code:

Calculate the number of documents in each category
 For each training document:
   	For each category:
    	If the entry appears in the document->Increase the count value of the entry
    	Increase the count value of all entries
 For each category:
 	For each entry:
 		The conditional probability is obtained by dividing the number of entries by the total number of entries
 Returns the conditional probability for each category

The code uses the characteristics of numpy in the implementation process.

And some places in this book are not clear:

For example:

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)  # element-wise mult
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

Why should log() be added when calculating P1 and P2? Why is it probability addition? Shouldn't it be multiplication?

CSDN boss gave the answer, absorbed and sorted it out:

When solving the underflow problem (precision will disappear when multiple extreme decimals are multiplied), so we can use l o g ( x ∗ y ) = l o g ( x ) + l o g ( y ) log(x*y)=log(x)+log(y) log(x * y)=log(x)+log(y).

The reason why it can be used is that the log function and probability function have the following distribution patterns:

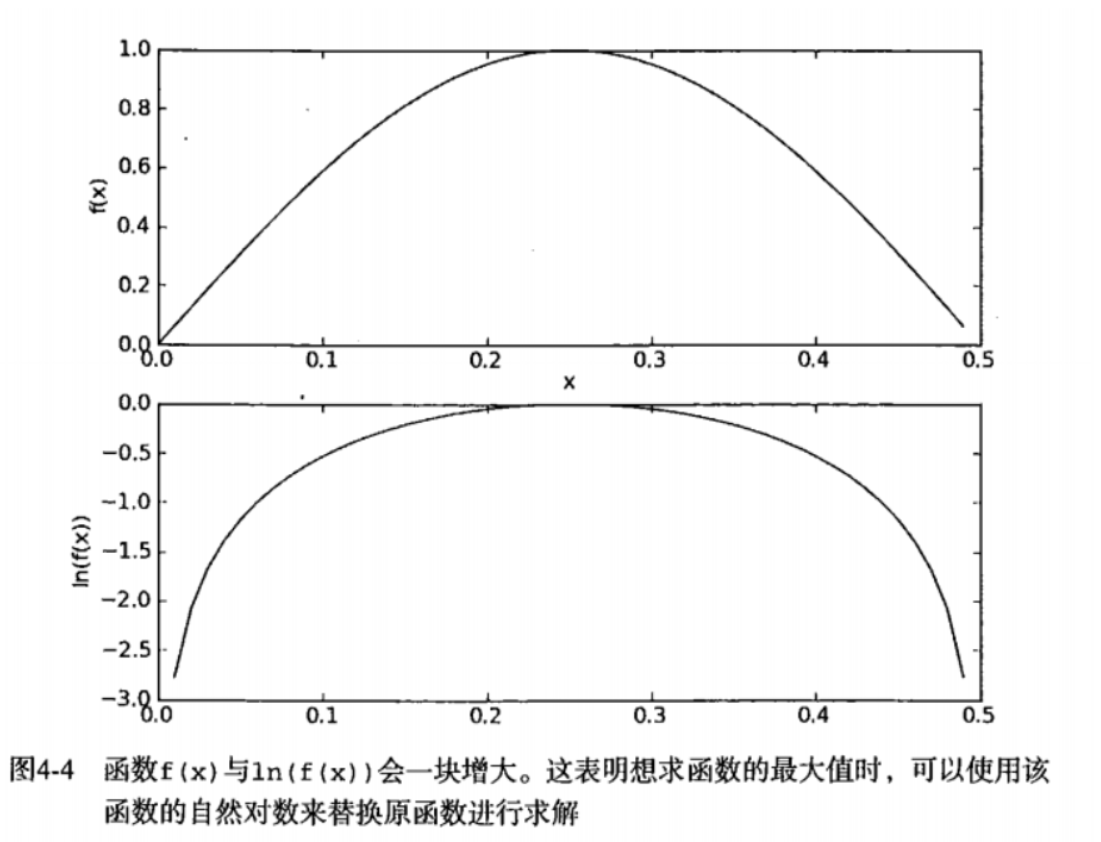
Then the above code is well explained.

Example: filtering spam using naive Bayes

Collect data: provide text files.
Prepare data: parse the text file into an entry vector.
Analyze data: check entries to ensure the correctness of parsing.
Training algorithm: use the training algorithm we established before trainNB0()Function.
Test algorithm: Using classifyNB(),And build a new test function to calculate the error rate of the document set.
Using algorithm: build a complete program to classify a group of documents and output the misclassified documents to the screen.

Text segmentation using regular expressions

import re
mySent='This book is the best book on python or M.L. i have ever laid eyes upon.'
regEx = re.compile('\\W')#\W represents a character that is not a word number
listOfTkens = regEx.split(mySent)#split() means to cut characters with mySent as the segmentation flag
to=[tok.lower() for tok in listOfTkens if len(tok)>0]#Remove the empty string with length 0, and the case does not affect the insult
print(listOfTkens)
print(to)

Retained cross validation: select a certain number from the data set as the test set, and the rest is used for training.

Example: using naive Bayesian classifier to obtain regional tendency from personal advertisement.

Data collection: from RSS To collect content from the source, you need to RSS Source build an interface
 Prepare data: parse the text file into an entry vector.
Analyze data: check entries to ensure the correctness of parsing.
Training algorithm: use the training algorithm we established before trainNB0()Function.
Test algorithm: observe the error rate to ensure that the classifier is available.
Using algorithm: build a complete program to classify a group of documents and output the misclassified documents to the screen.

The method of removing the most frequently occurring 30 words is used to reduce the error rate, which is caused by most of the redundancy in the language.

bayes.py

from numpy import *

#-----------------------------Conversion from thesaurus to vector------------------------------------
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # Label, 1 means insulting, 0 means No.
    return postingList, classVec

#---------------------------------Build dictionary-----------------------------------
def createVocabList(dataSet):
    vocabSet = set([])  # Get features
    for document in dataSet:
        vocabSet = vocabSet | set(document)  # union of the two sets
    return list(vocabSet)

#-------------------Check whether the features of the word vector to be classified appear in the dictionary------------------------
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)#Copy operation of list
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1#Word set model
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

#--------------------------Classifier training function---------------------------

def trainNB0(trainMatrix, trainCategory):#The former is the document word vector appearing in the dictionary, and the latter is the label vector
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory) / float(numTrainDocs)#P(c1)
    p0Num = ones(numWords)
    p1Num = ones(numWords)  # change to ones()
    p0Denom = 2.0
    p1Denom = 2.0  # In optimization, the probability is multiplied, but when one is 0, the overall probability will be 0 to prevent this phenomenon. Therefore, initialize the occurrence times of all words to 1 and the denominator to 2
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]#array type, which stores the number of occurrences of each word. It is added as a whole for convenience
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]#array type, which stores the number of occurrences of each word. It is added as a whole for convenience
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num / p1Denom)  # To solve the underflow problem, when multiple smaller numbers are multiplied, the value will be very small and the accuracy will be lost. Use the activation function to adjust the distribution
    p0Vect = log(p0Num / p0Denom)  # change to log(), the log function has similar characteristics to the probability density function, and there will be no underflow problem.
    return p0Vect, p1Vect, pAbusive


def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)  # element-wise mult
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

def testingNB():
    listOPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(thisDoc)
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))

def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1
    return returnVec

def textParse(bigString):  # input is big string, #output is word list
    import re
    listOfTokens = re.split(r'\W*', bigString)
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]


def spamTest():
    docList = []
    classList = []
    fullText = []
    for i in range(1, 26):
        wordList = textParse(open('email/spam/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList = textParse(open('email/ham/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList = createVocabList(docList)  # create vocabulary
    trainingSet = range(50)
    testSet = []  # create test set
    for i in range(10):
        randIndex = int(random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del (trainingSet[randIndex])
    trainMat = []
    trainClasses = []
    for docIndex in trainingSet:  # train the classifier (get probs) trainNB0
        trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses))
    errorCount = 0
    for docIndex in testSet:  # classify the remaining items
        wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
        if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
            errorCount += 1
            print("classification error", docList[docIndex])
    print('the error rate is: ', float(errorCount) / len(testSet))
    # return vocabList,fullText


def calcMostFreq(vocabList, fullText):
    import operator
    freqDict = {}
    for token in vocabList:
        freqDict[token] = fullText.count(token)
    sortedFreq = sorted(freqDict.items(), key=operator.itemgetter(1), reverse=True)
    return sortedFreq[:30]


def localWords(feed1, feed0):
    import feedparser
    docList = []
    classList = []
    fullText = []
    minLen = min(len(feed1['entries']), len(feed0['entries']))
    for i in range(minLen):
        wordList = textParse(feed1['entries'][i]['summary'])
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)  # NY is class 1
        wordList = textParse(feed0['entries'][i]['summary'])
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList = createVocabList(docList)  # create vocabulary
    top30Words = calcMostFreq(vocabList, fullText)  # remove top 30 words
    for pairW in top30Words:
        if pairW[0] in vocabList: vocabList.remove(pairW[0])
    trainingSet = range(2 * minLen)
    testSet = []  # create test set
    for i in range(20):
        randIndex = int(random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del (trainingSet[randIndex])
    trainMat = []
    trainClasses = []
    for docIndex in trainingSet:  # train the classifier (get probs) trainNB0
        trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses))
    errorCount = 0
    for docIndex in testSet:  # classify the remaining items
        wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
        if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
            errorCount += 1
    print('the error rate is: ', float(errorCount) / len(testSet))
    return vocabList, p0V, p1V


def getTopWords(ny, sf):
    import operator
    vocabList, p0V, p1V = localWords(ny, sf)
    topNY = []
    topSF = []
    for i in range(len(p0V)):
        if p0V[i] > -6.0:
            topSF.append((vocabList[i], p0V[i]))
        if p1V[i] > -6.0:
            topNY.append((vocabList[i], p1V[i]))
    sortedSF = sorted(topSF, key=lambda pair: pair[1], reverse=True)
    print("SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**")
    for item in sortedSF:
        print(item[0])
    sortedNY = sorted(topNY, key=lambda pair: pair[1], reverse=True)
    print("NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**")
    for item in sortedNY:
        print(item[0])

main.py

import re
import bayes
listOPosts,listClasses=bayes.loadDataSet()
myVocabList=bayes.createVocabList(listOPosts)
print(myVocabList)
print(bayes.setOfWords2Vec(myVocabList,listOPosts[0]))
trainMat = []
for postinDoc in listOPosts:
    trainMat.append(bayes.setOfWords2Vec(myVocabList,postinDoc))
print(trainMat)#What you get is the distribution of each sentence in the dictionary
p0v,p1v,pAb=bayes.trainNB0(trainMat,listClasses)
print(pAb)
print(p0v)
print(p1v)
bayes.testingNB()
mySent='This book is the best book on python or M.L. i have ever laid eyes upon.'
regEx = re.compile('\\W')#\W represents a character that is not a word number
listOfTkens = regEx.split(mySent)#split() means to cut characters with mySent as the segmentation flag
to=[tok for tok in listOfTkens if len(tok)>0]#Remove the empty string with length 0
print(listOfTkens)
print(to)

Conclusion:

• Using the knowledge of probability theory to classify things is a very natural idea. Based on the knowledge of statistics, a result is obtained, which is also an application of mathematical knowledge.
• The assumption of conditional independence between features is used in the modified model, which is also the reason why the probability can be obtained quickly. Although it is inconsistent with the facts, it performs very well on a specific data set. This method can be used as one of the model simplification methods.
• According to the redundancy of language, removing words with high frequency reduces the error rate, which is a good data preprocessing method.
• It is very skillful to solve the multiplier underflow problem by using the log() function.