1, Title Requirements

• Find all combinations of k numbers whose sum is n. only positive integers of 1 - 9 are allowed in the combination, and there are no duplicate numbers in each combination.
• explain:
• • All numbers are positive integers.
• • The solution set cannot contain duplicate combinations.
• Example 1:

input: k = 3, n = 7
 output: [[1,2,4]]

• Example 2:

input: k = 3, n = 9
 output: [[1,2,6], [1,3,5], [2,3,4]]

2, Solving algorithm

① Backtracking + pruning

• This problem is to find the combination of k numbers with sum n in the set [1,2,3,4,5,6,7,8,9], relative to [data structure and algorithm] there are K possible combination algorithms among the N numbers of [data structure and algorithm] , there is only one more limit. To find the combination of K numbers with sum of N, and the whole set is fixed [1,..., 9]. After understanding the possible combination algorithm of K numbers in N numbers, the problem is relatively simple.
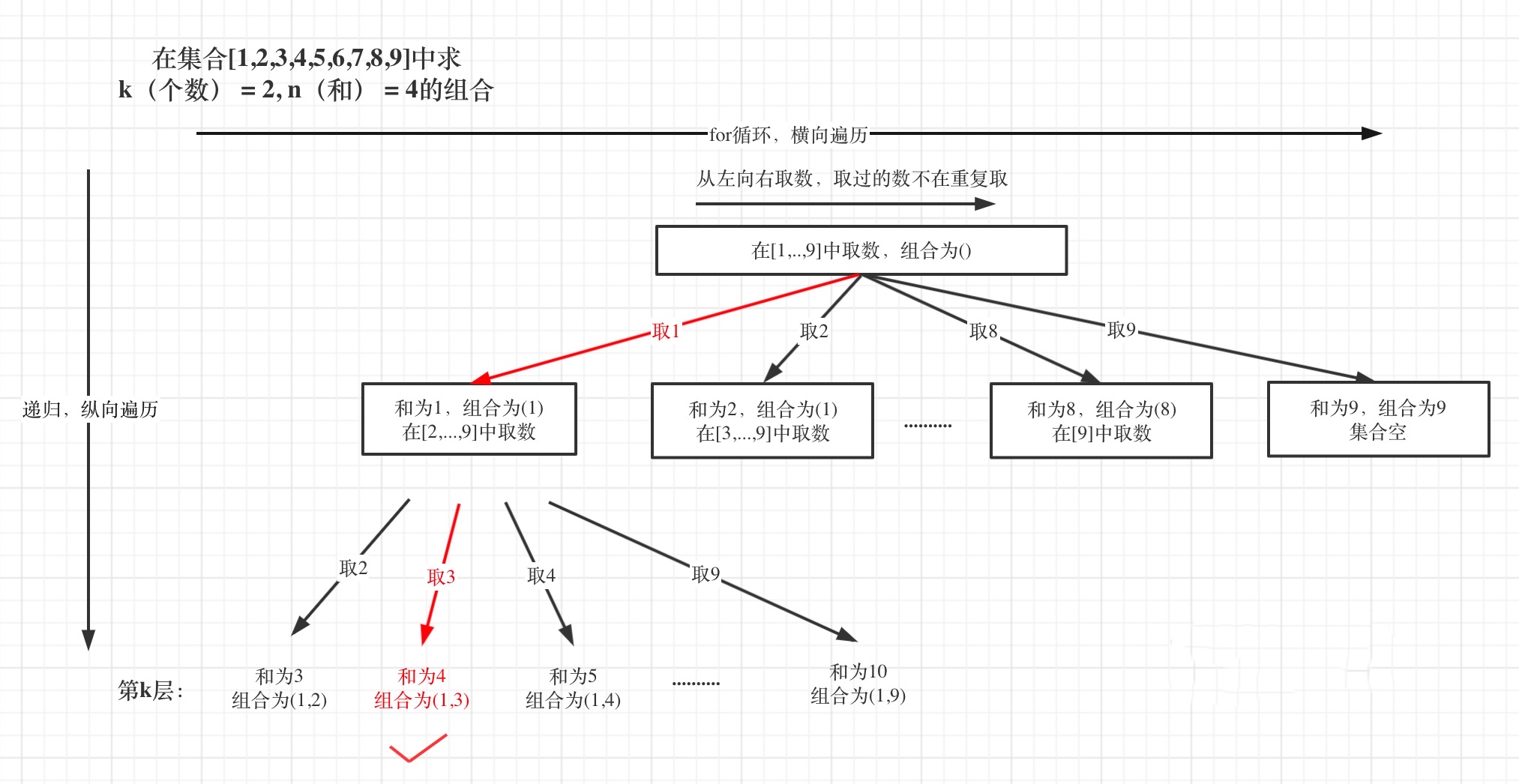
• K is equivalent to the depth of the tree, and 9 (because the whole set is the number of 9) is the width of the tree. For example, if k = 2 and n = 4, it is to find the combination of K (number) = 2 and n (sum) = 4 in the set [1,2,3,4,5,6,7,8,9].
• The selection process is shown in the figure below. It can be seen that only the last set (1, 3) and 4 meet the conditions:

• Retrospective Trilogy:
• • Determine recursive function parameters:
• • • and [data structure and algorithm] there are K possible combination algorithms among the N numbers of [data structure and algorithm] Similarly, you still need a one-dimensional array path to store qualified results, and a two-dimensional array result to store the result set. Here, you still define path and result as global variables. Why is it called path? From the tree structure above, we can see that the result is actually a path from root node to leaf node.

vector<vector<int>> result; // Store result set
vector<int> path; 			// Qualified results

• • • Next, the following parameters are required:
• • • • targetSum (int) target sum, that is, n in the topic;
• • • • k (int) is the set of k numbers required in the topic;
• • • • Sum (int) is the sum of the collected elements, that is, the sum of the elements in the path;
• • • • startIndex (int) is the starting position of the next for loop search.
• • • So the code is as follows:

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

• • • In fact, the sum parameter here can also be omitted. Subtract the selected element value from the targetSum each time, and then judge that if the targetSum is 0, it indicates that qualified results have been collected. Here, for the sake of intuition and understanding, a sum parameter is added. It should also be emphasized that it is difficult to determine the parameters of recursive function in backtracking method at one time. Generally, write logic first, and then fill in what parameters are needed.
• • Determine termination conditions:
• • • K actually limits the depth of the tree, because it takes k elements, and it makes no sense for the tree to go deeper, so if path If size () is equal to K, it terminates;
• • • If the elements collected in the path are the same as (sum) and targetSum (n of the Title Description), use result to collect the current results.
• • • Therefore, the termination code is as follows:

if (path.size() == k) {
    if (sum == targetSum) result.push_back(path);
    return; // If path Size () = = K but sum= Targetsum returns directly
}

• • Single layer search process:
• • • and [data structure and algorithm] there are K possible combination algorithms among the N numbers of [data structure and algorithm] One of the differences is that the set is fixed by 9 numbers [1,..., 9], so the for loop is fixed I < = 9:

• • • The processing process is to collect the elements selected each time by path, which is equivalent to the edges in the tree structure. Sum is used to count the sum of the elements in the path:

for (int i = startIndex; i <= 9; i++) {
    sum += i;
    path.push_back(i);
    backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts the startIndex
    sum -= i; 		 // to flash back
    path.pop_back(); // to flash back
}

• • Don't forget that the processing process and backtracking process correspond to each other one by one. If the processing is added, the backtracking must be reduced. Therefore, the C + + example is as follows:

class Solution {
private:
    vector<vector<int>> result; // Store result set
    vector<int> path; // Qualified results
    // targetSum: target sum, that is, n in the title.
    // k: A collection of K numbers required in the title.
    // Sum: the sum of the collected elements, that is, the sum of the elements in the path.
    // startIndex: the starting position of the next for loop search.
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // If path Size () = = K but sum= Targetsum returns directly
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; 		   // handle
            path.push_back(i); // handle
            backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts the startIndex
            sum -= i; 		 // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // Can not add
        path.clear();   // Can not add
        backtracking(n, k, 0, 1);
        return result;
    }
};

• C example:

int *path;
int pathTop;
int **result;
int resultTop;

void backTrack(int k,int n,int sum ,int startIndex){
    if(pathTop==k){
        if(n == sum){
            int *temp = malloc(sizeof(int)*k);
            for(int i =0;i<k;i++){
                temp[i] = path[i];
            }
            result[resultTop++] = temp;
        }
        return ;
    }
    for(int j=startIndex;j<=9-(k-pathTop)+1;j++){
        sum = sum + j;
        path[pathTop++] = j;
        backTrack(k,n,sum,j+1);
        sum = sum -j;
        pathTop--;
    }
}
int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
    pathTop = resultTop = 0;
    path = malloc(sizeof(int) *k);
    result = malloc(sizeof(int*) *100);
    backTrack(k,n,0,1);
    *returnSize = resultTop;
    *returnColumnSizes = malloc(sizeof(int*) * resultTop);
    for(int i=0 ; i<resultTop ; i++){
        (*returnColumnSizes)[i] = k;
    }
    return result;
}

• Then the pruning operation is easy to think of, as shown in the figure below:

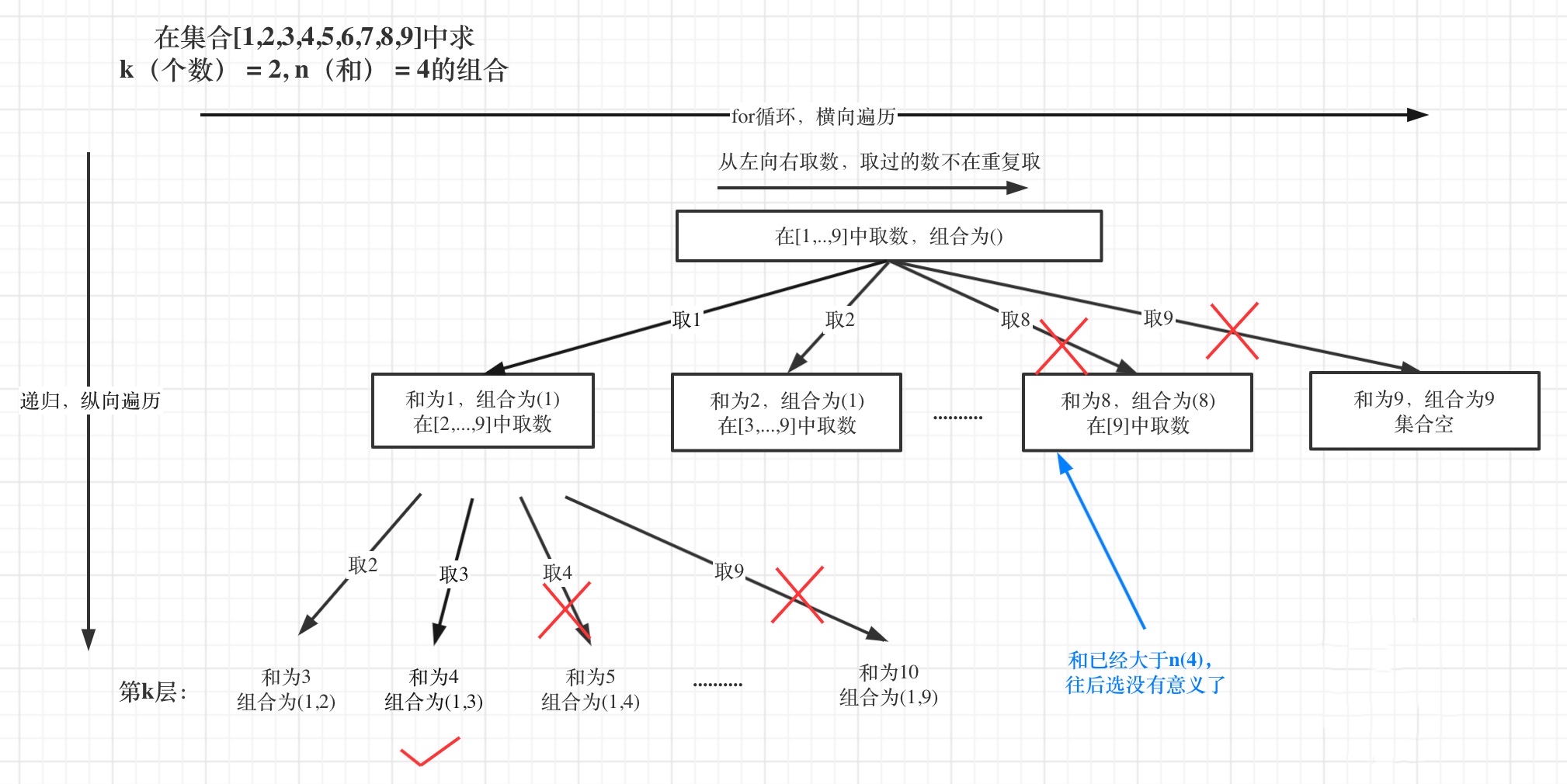
• If the sum of the selected elements is greater than n (the value in the figure is 4), it is meaningless to traverse back and cut them directly. The pruning place must be where the recursion terminates. The pruning code is as follows:

if (sum > targetSum) { // Pruning operation
    return;
}

• The final C + + example is as follows:

class Solution {
private:
    vector<vector<int>> result; // Store result set
    vector<int> path; // Qualified results
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) { // Pruning operation
            return; // If path Size () = = K but sum= Targetsum returns directly
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // prune
            sum += i; // handle
            path.push_back(i); // handle
            backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts the startIndex
            sum -= i; // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // Can not add
        path.clear();   // Can not add
        backtracking(n, k, 0, 1);
        return result;
    }
};

• Java example:

class Solution {
	List<List<Integer>> result = new ArrayList<>();
	LinkedList<Integer> path = new LinkedList<>();

	public List<List<Integer>> combinationSum3(int k, int n) {
		backTracking(n, k, 1, 0);
		return result;
	}

	private void backTracking(int targetSum, int k, int startIndex, int sum) {
		// Pruning
		if (sum > targetSum) {
			return;
		}

		if (path.size() == k) {
			if (sum == targetSum) result.add(new ArrayList<>(path));
			return;
		}
		
		// Pruning 9 - (k - path.size()) + 1
		for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
			path.add(i);
			sum += i;
			backTracking(targetSum, k, i + 1, sum);
			// to flash back
			path.removeLast();
			// to flash back
			sum -= i;
		}
	}
}

② Binary (subset) enumeration

• Only positive integers of 1 − 9 are allowed in the combination, and there are no duplicate numbers in each combination, which means that the combination contains at most
  9 numbers, we can convert the original problem into a set S={1,2,3,4,5,6,7,8,9}. To find the subset of S that meets the following conditions:
• • The size is k;
• • The sum of elements in the collection is n.
• Therefore, this problem can be solved by subset enumeration, that is, there are 9 numbers in the original sequence, and each number has two states, "selected to the subset" and "not selected to the subset", so the total number of States is 29. A 9-bit binary number mask is used to record the status of all current positions. From the first to the highest i bits, 0 means i is not selected into the subset, and 1 means i is selected into the subset. When all integers in [0, 29 − 1] are enumerated in sequence, each state can be enumerated to without repetition and omission. For a state mask, the corresponding subset sequence can be obtained by bit operation, and then judge whether the above two conditions are met. If they are satisfied, record the answer.
• How to get the information of each position of the mask through bit operation? For the ith position, you can judge whether the (1 < < i) & mask is 0. If it is not 0, it indicates that i is in the subset. Of course, it should be noted here that the range of a 9-bit binary number i is [0,8], and the optional number is [1,9], so we need to make a mapping. The simplest way is to add i+1 to the subset when we know that the position of i is not 0.
• Of course, subset enumeration can also be implemented recursively.
• C + + example:

class Solution {
public:
    vector<int> temp;
    vector<vector<int>> ans;

    bool check(int mask, int k, int n) {
        temp.clear();
        for (int i = 0; i < 9; ++i) {
            if ((1 << i) & mask) {
                temp.push_back(i + 1);
            }
        }
        return temp.size() == k && accumulate(temp.begin(), temp.end(), 0) == n; 
    }

    vector<vector<int>> combinationSum3(int k, int n) {
        for (int mask = 0; mask < (1 << 9); ++mask) {
            if (check(mask, k, n)) {
                ans.emplace_back(temp);
            }
        }
        return ans;
    }
};

• Java example:

class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        for (int mask = 0; mask < (1 << 9); ++mask) {
            if (check(mask, k, n)) {
                ans.add(new ArrayList<Integer>(temp));
            }
        }
        return ans;
    }

    public boolean check(int mask, int k, int n) {
        temp.clear();
        for (int i = 0; i < 9; ++i) {
            if (((1 << i) & mask) != 0) {
                temp.add(i + 1);
            }
        }
        if (temp.size() != k) {
            return false;
        }
        int sum = 0;
        for (int num : temp) {
            sum += num;
        }
        return sum == n;
    }
}

• Complexity analysis:
• • Time complexity: O(M) × 2m), where m is the size of the set. In this question, M is fixed as 9. There are 2m states in total. Each state requires the judgment of O(M+k)=O(M) (K ≤ m), so the time complexity is O(M) × 2M)；
• • Spatial complexity: O(M), that is, the spatial cost of temp.