Segment tree
Segment tree is a data structure commonly used to maintain interval information in algorithm competition. It is a basic and important data structure that an ACMer needs to master. The segment tree can realize single point modification, interval modification, interval query (interval summation, interval maximum value, minimum value, interval gcd) and other operations within the time complexity of O(logN)
Problem import:
Give you an array a with m operations. We now have $4 $operations:
1. Ask [L,R] interval sum
2. Ask [L,R] interval max
3. Modify a[pos] = new
4. Add x to each number of interval [L,R]
Array size 1e5, m size 1e5 (last introduction)
build (dichotomy)
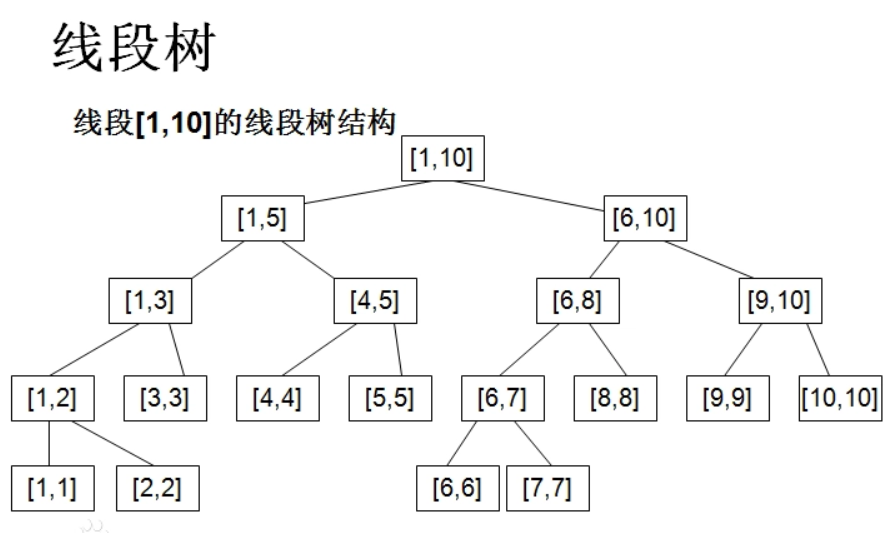
Code implementation:
Define an abstract tree with a structure:
const int N = 5e4+5;
int a[N];
//tree
struct Node
{
int l,r;//section
int sum;//Interval sum
int mid()//Intermediate value
{
return (l+r)/2;
}
}tre[4*N]; //Space to open 4 times!!! build function tree:
void build(int rt,int l,int r)
{
if(l==r)
{
tre[rt] = {l,r,a[l]};
}
else
{
tre[rt] = {l,r};//Assign a value to the interval of rt
int mid = tre[rt].mid();
//Be sure to put the push up last!
build(rt*2,l,mid);//Recursive left son
build(rt*2+1,mid+1,r);//Recursive right son
pushup(rt);//Recurse to the end point, start backtracking, and update the parent node by lson and rson
}
}Push up is a backtracking operation. The following describes the function and code implementation
Interval merge pushup function (backtracking)
Please see the following figure:
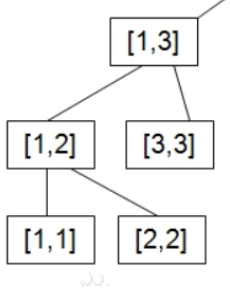
Assumptions:
[1,1]->1
[2,2]->2
[3,3]->3
[1, 2] = [1, 1] + [2, 2] = 3
[1,3] = [1,2]+[3,3] = 6
Rule: sum of father = sum of left son + sum of right son
Code implementation:
void pushup(int rt)//The push up operation updates the parent node information
{
//Left child + right child
tre[rt].sum = tre[rt*2].sum+tre[rt*2+1].sum;
}Interval query
Code implementation:
int query(int rt,int l,int r)
{
//If the query interval is strictly included in the interval [l,r] we want to find, return directly
if(tre[rt].l>=l&&tre[rt].r<=r)
return tre[rt].sum;
else
{
int mid = tre[rt].mid();
int ans = 0;
//If l < = current node mid, recursive lson
if(l<=mid) ans += query(rt*2,l,r);
//If r > = current node mid, recursive rson
if(r>mid) ans+=query(rt*2+1,l,r);
return ans;
}
}Single point modify
Code implementation:
//Modify modify (rt,x,pos) to add pos to the X node
void modify(int rt,int x,int pos)
{
if(tre[rt].l==x&&tre[rt].r==x)
tre[rt].sum += pos;
else
{
int mid = tre[rt].mid();
//If x is to the left of mid, recursive lson
if(x<=mid) modify(rt*2,x,pos);
//Conversely, on the right, recursive rson
else modify(rt*2+1,x,pos);
//Don't forget to update the parent node after updating x
pushup(rt);
}
}Let's try with an example!
Enemy troops array (classic example)
The topics are as follows:
Lily likes raising flowers very much, but because she has so many flowers, it's not easy to take care of them. She arranged her flowers in a row, and each pot had a beautiful value. If lily takes good care of a potted flower, the beauty value of the potted flower will rise. If she takes bad care of it, the beauty value of the potted flower will fall. Sometimes Lily wants to know the sum of the aesthetic values of a continuous flower, but Lily's arithmetic is not very good. Can you tell her the result quickly?
The first line is an integer T, indicating that there are t groups of test data.
The first line of each group of test data is a positive integer N (N < = 50000), indicating that Lily has N potted flowers.
Next, there are N positive integers, and the ith positive integer AI (1 < = AI < = 50) represents the initial aesthetic value of the ith potted flower.
Next, there is a command on each line. The command has four forms:
(1) Add i, J, i and j are positive integers, indicating that the ith potted flower is well cared for, and the aesthetic value increases J (J < = 30)
(2) Sub i, J, i and j are positive integers, indicating that the ith potted flower is not well cared for, and the aesthetic value is reduced by J (J < = 30)
(3) Query i, J, i and j are positive integers, i < = J, indicating the sum of aesthetic values from the ith potted flower to the jth potted flower
(4) End indicates the end. This command appears at the end of each group of data
There are no more than 40000 commands for each group of data
For group i data, first output "Case i:" and enter.
For each "Query i j" command, output the sum of the aesthetic values of the i-th potted flower to the j-th potted flower.
Sample Input
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
Sample Output
Case 1:
6
33
59
The AC code is as follows:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int N = 5e4+5;
int a[N];
//tree
struct Node
{
int l,r;//section
int sum;//Interval sum
int mid()//Intermediate value
{
return (l+r)/2;
}
}tre[4*N]; //Space to open 4 times!!!
void pushup(int rt)//The push up operation updates the parent node information
{
//Left child + right child
tre[rt].sum = tre[rt*2].sum+tre[rt*2+1].sum;
}
/*
build (rt,l,r)
Node number rt, left endpoint l, right endpoint r
*/
void build(int rt,int l,int r)
{
if(l==r)
{
tre[rt] = {l,r,a[l]};
}
else
{
tre[rt] = {l,r};//Assign a value to the interval of rt
int mid = tre[rt].mid();
//Be sure to put the push up last!
build(rt*2,l,mid);//Recursive left son
build(rt*2+1,mid+1,r);//Recursive right son
pushup(rt);//Recurse to the end point, start backtracking, and update the parent node by lson and rson
}
}
//query
int query(int rt,int l,int r)
{
//If the query interval is strictly included in the interval [l,r] we want to find, return directly
if(tre[rt].l>=l&&tre[rt].r<=r)
return tre[rt].sum;
else
{
int mid = tre[rt].mid();
int ans = 0;
//If l < = current node mid, recursive lson
if(l<=mid) ans += query(rt*2,l,r);
//If r > = current node mid, recursive rson
if(r>mid) ans+=query(rt*2+1,l,r);
return ans;
}
}
//Modify modify (rt,x,pos) to add pos to the X node
void modify(int rt,int x,int pos)
{
if(tre[rt].l==x&&tre[rt].r==x)
tre[rt].sum += pos;
else
{
int mid = tre[rt].mid();
//If x is to the left of mid, recursive lson
if(x<=mid) modify(rt*2,x,pos);
//Conversely, on the right, recursive rson
else modify(rt*2+1,x,pos);
//Don't forget to update the parent node after updating x
pushup(rt);
}
}
int main()
{
int t;
scanf("%d",&t);
int cnt = 1;
while(t--)
{
printf("Case %d:\n",cnt++);
int n;
scanf("%d",&n);
for(int i = 1;i<=n;i++)
scanf("%d",&a[i]);
build(1,1,n);
while(1)
{
char ch[10];
int a,b;
scanf("%s",ch);
if(ch[0]=='E')
break;
scanf("%d %d",&a,&b);
if(ch[0]=='Q')
printf("%d\n",query(1,a,b));
else if(ch[0]=='A')
modify(1,a,b);
else
modify(1,a,-b);
}
}
} Interval modification
Think about it. If you use single point modification to modify an interval and add a pos to the interval, a single point modification is the complexity of logn, and the interval is the largest, that is [1, n], then the complexity of an interval modification will reach nlog(n). It's too difficult to bear. It's better to use violent for loop. In order to solve this problem, use interval modification, It can help us complete interval modification with the complexity of logn
if(tre[rt].l>=l&&tre[rt].r<=r ) return tre[rt].sum
If we encounter a complete interval, we don't need to go on. Just return here, which reduces many branches and greatly reduces the time complexity. Is it the same reason for us to modify? If I want to add a number to this complete interval, I just need to mark lazy on this node, and I won't go on the following road. When to go there? When I start to ask the child nodes affected by this node, do I have to add all the lazys related to their parent nodes? I will follow the direction of query and lower this lazy. Then the sum of the last accesses is right. In this way, I can complete the interval modification with O(logn) complexity
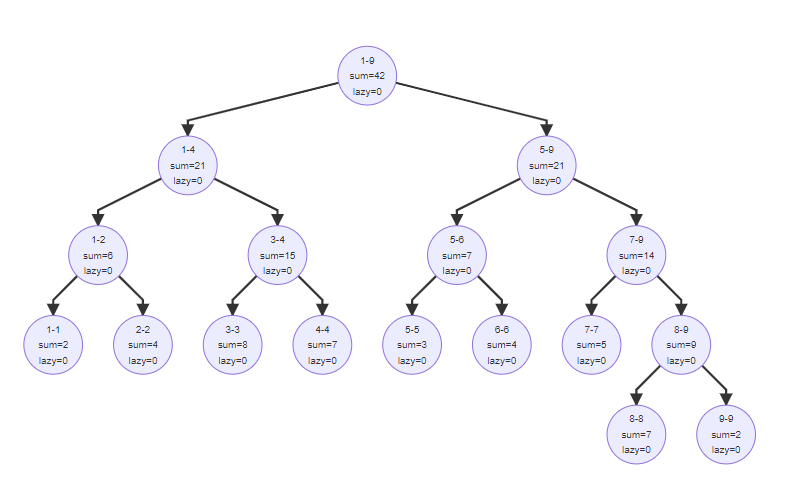
Introducing new variables
On the basis of the above, we introduce a new thing: lazy. This lazy represents the amount we modify the current interval. Now we strictly define sum: sum represents the sum of the current interval. Lazy: lazy flag. Add the number of lazy to each node in the subtree with the current node rt as the root (emphasize that the root node is not included)
Achievements:
Push down
Code implementation:
void pushdown(int rt)
{
if(tre[rt].lazy)
{
tre[rt<<1].lazy+=tre[rt].lazy;// Pass the lazy of the parent node rt to the left and right sons
tre[rt<<1|1].lazy+=tre[rt].lazy;
tre[rt<<1].sum+=(tre[rt<<1].r-tre[rt<<1].l+1)*tre[rt].lazy;// sum is the interval length * parent node lazy
tre[rt<<1|1].sum+=(tre[rt<<1|1].r-tre[rt<<1|1].l+1)*tre[rt].lazy;
tre[rt].lazy = 0;// Don't forget to empty lazy
}
}Why don't I include the root node?
Let me ask you a question. If I add 10 to the interval on 3-4 for the first time, and then add 12 to the interval on 4-5. If my lazy has not been delegated before, is there a problem? Is there a conflict between adding 10 or adding 12 to my 4 node. If there is a conflict, the explanation is wrong. How to solve the conflict? When we visit a node, we should also delegate his lazy to their son to explain clearly. Don't leave this problem to his father
Interval query
Code implementation:
ll query(int rt,int l,int r)
{
if(tre[rt].l>=l&&tre[rt].r<=r)
return tre[rt].sum;
else
{
pushdown(rt);
ll ans = 0;
int mid = tre[rt].mid();
if(l<=mid) ans+=query(rt<<1,l,r);
if(r>mid) ans+=query(rt<<1|1,l,r);
return ans;
}
}Let's try with an example!
The topics are as follows:
A Simple Problem with Integers
The captain gives a sequence. If you want to help the captain, you need to deal with the following two situations.
"C a b c" means that all values in [a, b] interval are increased by c (-10000 ≤ c ≤ 10000).
"Q a b" asks the sum of all values in the [a, b] interval.
The first line contains two integers N, Q. 1 ≤ N,Q ≤ 100000.
The second line contains n integers representing the initial sequence A (-1000000000 ≤ Ai ≤ 1000000000).
Next, ask in line Q in the format of the title description.
For each question beginning with Q, you need to output the corresponding answer, one line for each answer.
Sample Input
10 5 1 2 3 4 5 6 7 8 9 10 Q 4 4 Q 1 10 Q 2 4 C 3 6 3 Q 2 4
Sample Output
4 55 9 15
The AC code is as follows:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
const int N = 1e5+9;
ll a[N];
struct nn
{
int l,r;
ll sum;
ll lazy;
int mid()
{
return l+r>>1;
}
}tre[4*N];
void pushup(int rt)
{
tre[rt].sum = tre[rt<<1].sum+tre[rt<<1|1].sum;
}
void pushdown(int rt)
{
if(tre[rt].lazy)
{
tre[rt<<1].lazy+=tre[rt].lazy;
tre[rt<<1|1].lazy+=tre[rt].lazy;
tre[rt<<1].sum+=(tre[rt<<1].r-tre[rt<<1].l+1)*tre[rt].lazy;
tre[rt<<1|1].sum+=(tre[rt<<1|1].r-tre[rt<<1|1].l+1)*tre[rt].lazy;
tre[rt].lazy = 0;
}
}
void build(int rt,int l,int r)
{
if(l==r)
tre[rt] = {l,r,a[l],0};
else
{
tre[rt] = {l,r};
int mid = tre[rt].mid();
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
pushup(rt);
}
}
ll query(int rt,int l,int r)
{
if(tre[rt].l>=l&&tre[rt].r<=r)
return tre[rt].sum;
else
{
pushdown(rt);
ll ans = 0;
int mid = tre[rt].mid();
if(l<=mid) ans+=query(rt<<1,l,r);
if(r>mid) ans+=query(rt<<1|1,l,r);
return ans;
}
}
void modify(int rt,int l,int r,ll v)
{
if(tre[rt].l>=l&&tre[rt].r<=r)
{
tre[rt].lazy+=v;
tre[rt].sum+=(tre[rt].r-tre[rt].l+1)*v;
}
else
{
pushdown(rt);
int mid = tre[rt].mid();
if(l<=mid) modify(rt<<1,l,r,v);
if(r>mid) modify(rt<<1|1,l,r,v);
pushup(rt);
}
}
int main()
{
int n,m;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;i++)
scanf("%lld",&a[i]);
build(1,1,n);
while(m--)
{
int l,r;
ll v;
char ch[10];
scanf("%s %d %d",ch,&l,&r);
if(ch[0]=='Q')
printf("%lld\n",query(1,l,r));
else
{
scanf("%lld",&v);
modify(1,l,r,v);
}
}
} Finally, thank you for reading!!!
