1, Definition and characteristics
A stack is a linear table that performs insertion and deletion operations only at one end of the table (a linear table refers to a one-to-one relationship between elements rather than sequential storage and chain storage). The operation end is called the top of the stack and the other end is called the bottom of the stack.
It can be seen from the above that the elements that enter the stack first are pressed at the bottom of the stack and then come out, and the elements that enter the stack later come out first at the top of the stack. Therefore, the stack has the characteristics of last in first out.
2, Two implementations of stack
(1) Sequential stack
public class MyStack {
private int[] arr; // Arrays are used at the bottom of the sequential stack
private int maxSize; // Maximum capacity
private int top; // Stack top pointer
// Constructor is also the initialization of the stack
public MyStack(int maxSize) {
arr = new int[maxSize];
this.maxSize = maxSize;
top = -1;
}
// Judge stack full
private boolean isFull() {
return top == maxSize - 1;
}
// Judge stack empty
private boolean isEmpty() {
return top == -1;
}
// Before entering the stack, you need to judge whether the stack is full
public void push(int num) {
if (isFull()) {
System.out.println("Stack full!");
return;
}
arr[++top] = num;
}
// To exit the stack, you need to first judge whether the stack is empty
public int pop() {
if (isEmpty()) {
System.out.println("Stack empty!");
return -1; // return -1 here does not mean to return the real value in the stack. It is only a mark returned when the stack is empty
}
return arr[top--];
}
// Take the stack top element, and the stack top pointer remains unchanged
public int getPeak() {
if (isEmpty()) {
System.out.println("Stack empty!");
return -1;
}
return arr[top];
}
// Output all elements in the stack, bottom of stack -- > top of stack
public void printAll() {
int bottom = 0;
for (; bottom <= top; bottom++) {
System.out.println(arr[bottom]);
}
}
// Gets the number of elements in the stack
public int getSize() {
return top + 1;
}
}
(2) Chain stack
public class MyStack {
// Internal class, used to create a new node
private class Node {
int data;
Node next;
public Node(int data) {
this.data = data;
}
}
// The bottom layer of the chain stack uses a single linked list. Because the single linked list is unidirectional and the stack operation is only at the top of the stack, the header of the single linked list is the top of the chain stack
private Node top;
// Count the number of elements in the stack
private int size;
// Constructor, which is also initialization, makes the stack top pointer null. Because the member variable has a default value, the constructor can also not write
public MyStack() {
top = null;
size = 0;
}
// Compared with sequential stack, there is no need to judge whether the stack is full
public void push(int input) {
Node node = new Node(input);
if (top == null) {
top = node;
} else {
node.next = top;
top = node;
}
size++;
}
// To exit the stack, you need to judge whether the stack is empty
public int pop() {
if (top == null) {
System.out.println("Stack empty!");
return -1; // return -1 is also an empty stack flag
} else {
/*
* The following code should also free up the space of the top element of the stack, but because there is a reference relationship in java, setting the top to null only disconnects the address of the referenced object
* And java has its own garbage collection mechanism, so it will not be released temporarily
*/
int num = top.data;
top = top.next;
size--;
return num;
}
}
// Get stack top element
public int getPeak() {
if (top == null) {
System.out.println("Stack empty!");
return -1;
} else {
return top.data;
}
}
// Output all elements in the stack. Because the single linked list used by the bottom layer, it can only be used at the top -- > bottom of the stack
public void printAll() {
Node node = top;
while (node != null) {
System.out.println(node.data);
node = node.next;
}
}
// Gets the total number of elements in the stack
public int getSize() {
return size;
}
}
3, Stack and recursion
(1) Recursion
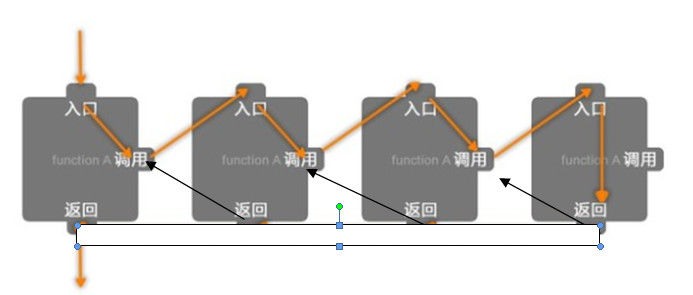
To put it simply, the function itself is called inside a function, and the calling function can be executed only after the operation result of the called function. As described in the figure below
Conditions for recursion:
1. The solution of a problem can be decomposed into the solutions of several subproblems, and the solution idea of this problem is exactly the same as that of the decomposed subproblem except for the data scale or processing object. The data scale or processing object of the subproblem is smaller and changes regularly.
2. The decomposition must be finite times, that is, there is a recursive termination condition, that is, recursive exit.
(2) Recursion and recursive work stack
In the high-level language, the information exchange between the calling function and the called function is carried out through the stack. For example, function A calls the function B, then we need to save some variable information of A and call the function B. After the B is called to get the return value, the program still has to go back to the A of the letter number, so we must pop the variable information of B. Otherwise, you can't get the variable information of A.
Generally, when a function calls another function during operation, the system must complete three things before running the called function:
(1) Pass all arguments, return address and other information to the called function for saving;
(2) Allocate a storage area for the local variables of the called function;
(3) Transfer control to the entry of the called function.
Before returning from the called function to the calling function, the system also needs to complete three things:
(1) Save the operation results of the called function;
(2) Release the data area of the called function;
(3) Transfer control to the calling function according to the return address saved by the called function.
When multiple functions form nested calls, according to the principle of "post invocation first return", the system arranges the data space needed for the whole program to run in a stack, and when it calls a function, it assigns a storage area to the top of the stack. Whenever a function exits, its storage area is released; Therefore, the data area of the currently running function must be at the top of the stack.
The running process of a recursive function is similar to the nested call of a function, except that the called function is itself. Therefore, a very important parameter of a recursive function is its recursive level, because the recursive level directly affects the size of the system work stack.
(3) Using stack to convert recursion to non recursion
When the recursive function is executed, the system provides an implicit stack to save the information of each function, and rewriting the recursive function into non recursive is actually to actively open up a stack and use this stack to simulate the recursive process.
During recursion, when each function is called, there are only the following two cases:
(1) Must be executed if the execution conditions are met;
(2) If the execution conditions are not met, for example, other functions are called inside the function, the function can be executed only after the return result of the called function. In this case, the execution needs to be suspended. First, its local variables, return address and other function information need to be pushed into the stack.
Therefore, the general steps of eliminating recursion by stack can be summarized as follows:
(1) Set a work stack to store recursive work records (including arguments, return addresses, local variables, etc.).
(2) Enter the non recursive call entry (i.e. the beginning of the called program), and put the arguments and return address passed by the calling program on the stack (the recursive program can not be used as the main program, so it can be considered that it was initially called by a calling program).
(3) Enter the recursive call entry: when the recursive end conditions are not met, recurse layer by layer and put the arguments, return addresses and local variables on the stack. This process can be realized by circular statements -- simulating the recursive decomposition process.
(4) If the recursion end condition is satisfied, the given constant reaching the recursion exit is taken as the current function value.
(5) Return processing: when the stack is not empty, exit the stack top record repeatedly, and carry out the operation specified in the title according to the return address in the record, that is, calculate the current function value layer by layer until the stack is empty - simulate the recursive evaluation process.
The above manual copy of data structure C language version 2. If you don't understand, please refer to this blog: Blog address . (a great explanation, recommend it ~)
His description is:
(1) First, you need to build your own stack. What the stack holds is a record, including the values of all local variables and the location of the code executed.
(2) Then initialize the local variable to the initial state, and then enter the main loop.
(3) When executing code, if recursion is encountered, the state is made and saved on the stack, and then the local variables are updated to the next level. If a call ends, it returns to the upper state. Directly pop up the records in the stack to update the current status.
(4) At the end of a call, if the stack is empty, all calls end and exit the main loop.
In short, any recursive type can be rewritten to non recursive according to the above steps.
See details for specific implementation Non recursive traversal of binary trees.