This series describes the random number API before Java 17 and the unified API after Java 17 in detail, and makes some simple analysis on the characteristics and implementation ideas of random numbers to help you understand why there are so many random number algorithms and their design ideas.
This series will be divided into two parts. The first part describes the evolution ideas, underlying principles and considerations of java random number algorithm, and then introduces the random number algorithm API and test performance before Java 17. The second part analyzes the random number generator algorithm, API and underlying implementation classes after Java 17, as well as their properties, performance and use scenarios, how to select random algorithms, etc, The application of java random number to some future features of Java is prospected
This is the second article
Changes after Java 17
Disadvantages of previous API s
- There is no unified interface: the previous Random and SplittableRandom have no unified inheritance classes and unified abstract interfaces. Although their internal methods are basically the same and there is not much trouble in replacing each other, it is also troublesome for us to implement our own Random algorithms because there is no unified interface.
- ThreadLocalRandom has poor compatibility with the virtual threads of the future project room. Virtual threads are resources that can be created continuously. In a large number of virtual threads, if ThreadLocalRandom is still used for one-to-one correspondence, the randomness will be weakened. Therefore, we need to find new implementation methods and pave the way for project room from now on.
New API definition
In Java 17 JEP 356: Enhanced Pseudo-Random Number Generators In, the interface of random number generator, RandomGenerator, is unified:
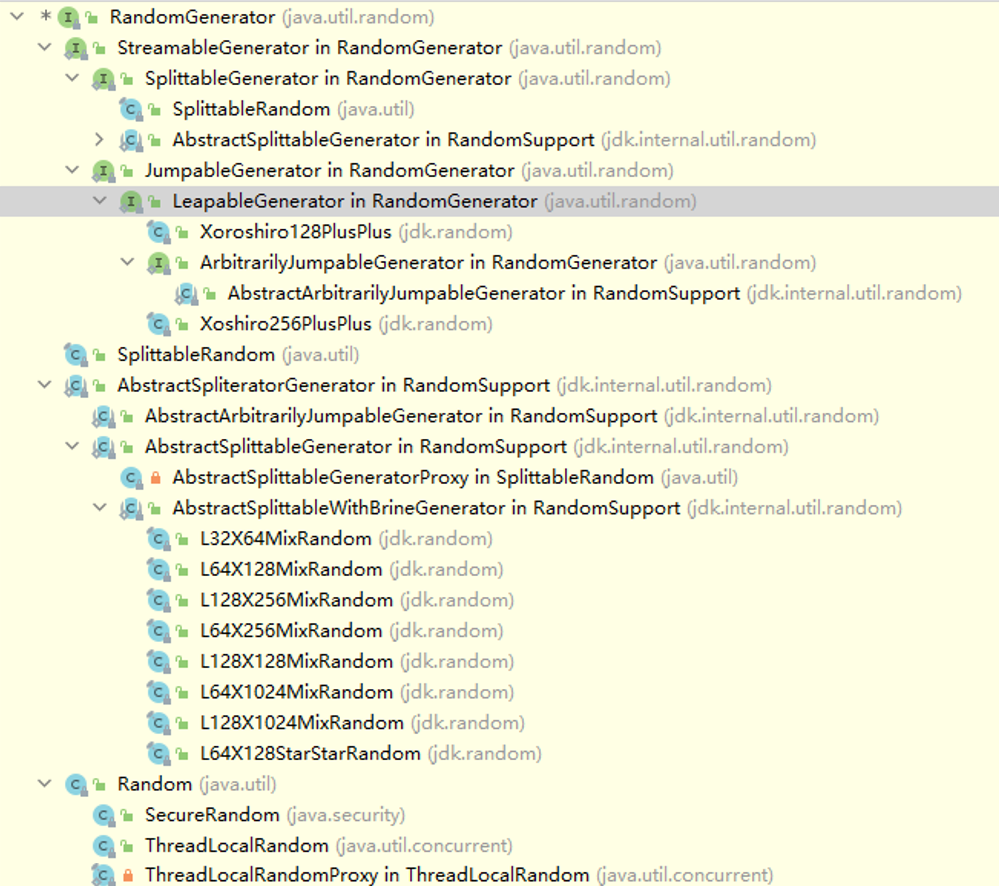
Among them, the corresponding interface JumpableGenerator is abstracted for the hoppability mentioned earlier (many elements in the sequence ring can be skipped through simple calculation). If the hopping step size wants to be larger, the corresponding interface is LeapableGenerator.
The interface SplitableGenerator is also abstracted for the splittability mentioned earlier (random number generators that can be split into completely different sequences through simple calculation)
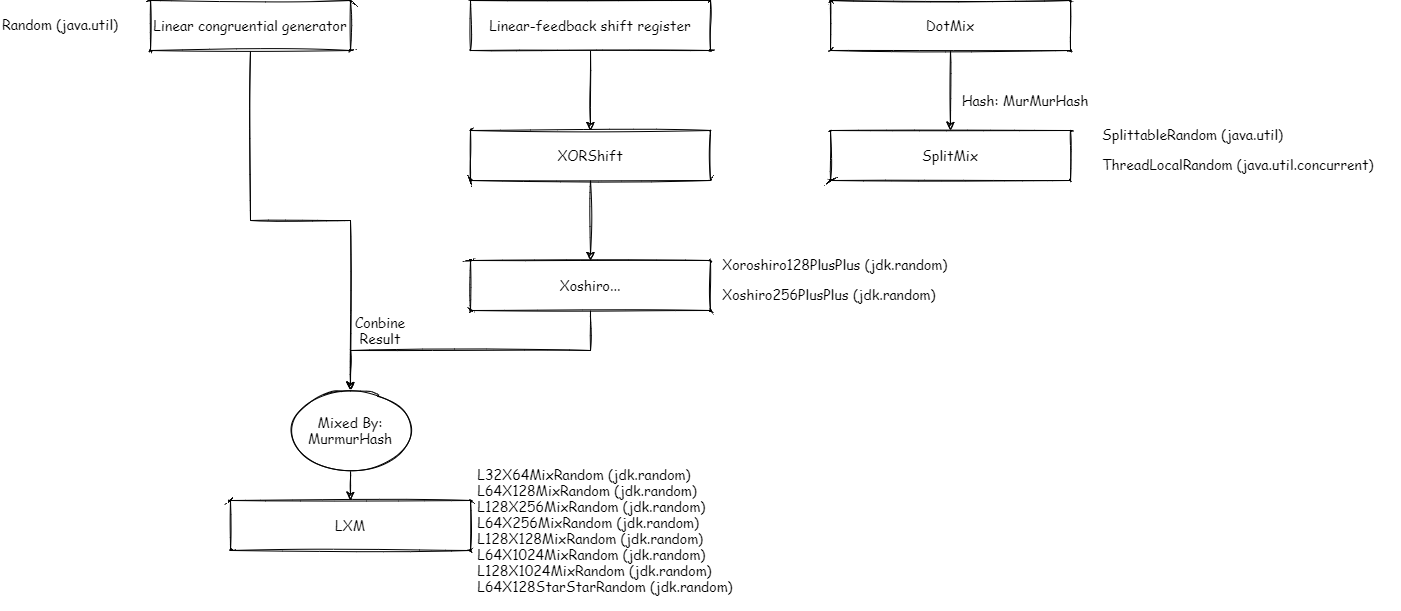
The algorithms mentioned above and the corresponding implementation classes are:
After unifying the abstraction, we can create random number generators of different implementation types in this way:
RandomGenerator random = RandomGeneratorFactory.of("Random").create();
RandomGenerator secureRandom = RandomGeneratorFactory.of("SecureRandom").create();
RandomGenerator splittableRandom = RandomGeneratorFactory.of("SplittableRandom").create();
RandomGenerator xoroshiro128PlusPlus = RandomGeneratorFactory.of("Xoroshiro128PlusPlus").create();
RandomGenerator xoshiro256PlusPlus = RandomGeneratorFactory.of("Xoshiro256PlusPlus").create();
RandomGenerator l64X256MixRandom = RandomGeneratorFactory.of("L64X256MixRandom").create();
RandomGenerator l64X128StarStarRandom = RandomGeneratorFactory.of("L64X128StarStarRandom").create();
RandomGenerator l64X128MixRandom = RandomGeneratorFactory.of("L64X128MixRandom").create();
RandomGenerator l64X1024MixRandom = RandomGeneratorFactory.of("L64X1024MixRandom").create();
RandomGenerator l32X64MixRandom = RandomGeneratorFactory.of("L32X64MixRandom").create();
RandomGenerator l128X256MixRandom = RandomGeneratorFactory.of("L128X256MixRandom").create();
RandomGenerator l128X128MixRandom = RandomGeneratorFactory.of("L128X128MixRandom").create();
RandomGenerator l128X1024MixRandom = RandomGeneratorFactory.of("L128X1024MixRandom").create();
The properties of the random number generator class implemented by each algorithm
1.Random: the bottom layer is a 48 bit number generated based on the linear congruence algorithm. The selected parameters ensure that each number can be randomly selected, so the Period is 2 ^ 48. Neither nextInt nor nextLong can achieve a completely uniform random distribution, because the generated number is a 48 bit number, nextInt is 32 bits, and nextLong is combined twice. In the previous algorithm analysis, we mentioned that this algorithm can not jump or segment.
2.SplittableRandom: a 64 bit number generated by the underlying SplitMix algorithm. MurMurhash ensures that every number in the interval will appear (so the Period is 2 ^ 64) and is completely evenly distributed. For nextInt, each result will appear twice in a Period, and for nextLong, each result will appear once in a Period. In the previous algorithm analysis, we mentioned that this algorithm can not jump and can be segmented.
3.Xoroshiro128PlusPlus: the bottom layer is based on the Xoroshiro128 + + algorithm and uses two 64 bit numbers to record the status. These two numbers will not be 0 at the same time. After calculation, these two numbers are combined into a 64 bit random number. Because it is a combination of two 64 bit numbers, there are 2 ^ 64 * 2 ^ 64 = 2 ^ 128 different combinations. The two numbers will not be 0 at the same time, so there is one less case. Therefore, there are 2 ^ 128 - 1 cases in total, so the Period is 2 ^ 128 - 1. In the previous algorithm analysis, we mentioned that this algorithm can jump and cannot be segmented.
4.Xoshiro256PlusPlus: the bottom layer is based on the Xoshiro256 + + algorithm and uses four 64 bit numbers to record the status. These four numbers will not be 0 at the same time. After calculation, these four numbers are combined into a 64 bit random number. Because it is composed of four 64 bit numbers, there are 2 ^ 64 * 2 ^ 64 * 2 ^ 64 * 2 ^ 64 = 2 ^ 256 different combinations. The two numbers will not be 0 at the same time, so there is one less case. Therefore, there are 2 ^ 256 - 1 cases in total, so the Period is 2 ^ 256 - 1. In the previous algorithm analysis, we mentioned that this algorithm can jump and cannot be segmented.
5. L64X256MixRandom: Based on the LXM algorithm, the bottom layer uses a 64 bit number to save the results of linear congruence. Four 64 bit numbers record Xoshiro combinations. There are 2 ^ 64 different combinations of linear congruence and 2 ^ 256 - 1 combinations of Xoshiro. There are 2 ^ 64 (2 ^ 256 - 1) combinations in total, so the Period is 2 ^ 64 (2 ^ 256 - 1). In the previous algorithm analysis, we mentioned that this algorithm can be segmented without jumping.
Other LXM implementation classes are similar.

In fact, these attributes can be seen from the annotation of the implementation class of each algorithm:
@Retention(RetentionPolicy.RUNTIME)
@Target(ElementType.TYPE)
public @interface RandomGeneratorProperties {
/**
* Algorithm name
*/
String name();
/**
* Algorithm category
*/
String group() default "Legacy";
/**
* period The size is described by three numbers I, J and K, namely:
* period = (2^i - j) * 2^k
*/
int i() default 0;
int j() default 0;
int k() default 0;
/**
* Uniform distribution. 0 or the maximum value is not uniform distribution. This value describes how many times each number occurs in a Period, but it is not so accurate. Some small deviations will be ignored. For example, Xoroshiro128 + + thinks that each number occurs 2 ^ 64 times instead of 2 ^ 64 - 1 times.
*/
int equidistribution() default Integer.MAX_VALUE;
/**
* Is it an algorithm based on system Entropy (refer to the previous SEED source Chapter)
*/
boolean isStochastic() default false;
/**
* Is it a hardware assisted algorithm
*/
boolean isHardware() default false;
}
We can also view the properties of each implementation through the following code. Similarly, we can filter the algorithm through these API s to find the implementation class suitable for our business:
RandomGeneratorFactory.all()
.map(fac -> fac.group()+":"+fac.name()
+ " {"
+ (fac.isSplittable()?" splitable":"")
+ (fac.isStreamable()?" streamable":"")
+ (fac.isJumpable()?" jumpable":"")
+ (fac.isLeapable()?" leapable":"")
+ (fac.isHardware()?" hardware":"")
+ (fac.isStatistical()?" statistical":"")
+ (fac.isStochastic()?" stochastic":"")
+ " stateBits: "+fac.stateBits()
+ " }"
)
.sorted().forEach(System.out::println);
The output is:
LXM:L128X1024MixRandom { splitable streamable statistical stateBits: 1152 }
LXM:L128X128MixRandom { splitable streamable statistical stateBits: 256 }
LXM:L128X256MixRandom { splitable streamable statistical stateBits: 384 }
LXM:L32X64MixRandom { splitable streamable statistical stateBits: 96 }
LXM:L64X1024MixRandom { splitable streamable statistical stateBits: 1088 }
LXM:L64X128MixRandom { splitable streamable statistical stateBits: 192 }
LXM:L64X128StarStarRandom { splitable streamable statistical stateBits: 192 }
LXM:L64X256MixRandom { splitable streamable statistical stateBits: 320 }
Legacy:Random { statistical stateBits: 48 }
Legacy:SecureRandom { stochastic stateBits: 2147483647 }
Legacy:SplittableRandom { splitable streamable statistical stateBits: 64 }
Xoroshiro:Xoroshiro128PlusPlus { streamable jumpable leapable statistical stateBits: 128 }
Xoshiro:Xoshiro256PlusPlus { streamable jumpable leapable statistical stateBits: 256 }
Which algorithm is the fastest (it is obvious without testing)
According to the previous analysis, SplittableRandom is the fastest in a single threaded environment and ThreadLocalRandom is the fastest in a multi-threaded environment. The new random algorithm implementation class, Period, requires more calculations, and the implementation of LXM requires more calculations. These algorithms are added to adapt to more random applications, not faster. However, in order to satisfy everyone's curiosity, the following code is written for testing. It can also be seen from the following code that the new RandomGenerator API is easier to use:
package prng;
import java.util.random.RandomGenerator;
import java.util.random.RandomGeneratorFactory;
import org.openjdk.jmh.annotations.Benchmark;
import org.openjdk.jmh.annotations.BenchmarkMode;
import org.openjdk.jmh.annotations.Fork;
import org.openjdk.jmh.annotations.Measurement;
import org.openjdk.jmh.annotations.Mode;
import org.openjdk.jmh.annotations.Param;
import org.openjdk.jmh.annotations.Scope;
import org.openjdk.jmh.annotations.Setup;
import org.openjdk.jmh.annotations.State;
import org.openjdk.jmh.annotations.Threads;
import org.openjdk.jmh.annotations.Warmup;
import org.openjdk.jmh.infra.Blackhole;
import org.openjdk.jmh.runner.Runner;
import org.openjdk.jmh.runner.RunnerException;
import org.openjdk.jmh.runner.options.Options;
import org.openjdk.jmh.runner.options.OptionsBuilder;
//The test index is throughput
@BenchmarkMode(Mode.Throughput)
//Preheating is required to eliminate the impact of jit real-time compilation and JVM collection of various indicators. Since we cycle many times in a single cycle, preheating once is OK
@Warmup(iterations = 1)
//Number of threads
@Threads(10)
@Fork(1)
//Test times, we test 50 times
@Measurement(iterations = 50)
//The life cycle of a class instance is defined, and all test threads share an instance
@State(value = Scope.Benchmark)
public class TestRandomGenerator {
@Param({
"Random", "SecureRandom", "SplittableRandom", "Xoroshiro128PlusPlus", "Xoshiro256PlusPlus", "L64X256MixRandom",
"L64X128StarStarRandom", "L64X128MixRandom", "L64X1024MixRandom", "L32X64MixRandom", "L128X256MixRandom",
"L128X128MixRandom", "L128X1024MixRandom"
})
private String name;
ThreadLocal<RandomGenerator> randomGenerator;
@Setup
public void setup() {
final String finalName = this.name;
randomGenerator = ThreadLocal.withInitial(() -> RandomGeneratorFactory.of(finalName).create());
}
@Benchmark
public void testRandomInt(Blackhole blackhole) throws Exception {
blackhole.consume(randomGenerator.get().nextInt());
}
@Benchmark
public void testRandomIntWithBound(Blackhole blackhole) throws Exception {
//Note that the number 2^n is not taken, because this number is generally not used as the scope of practical application, but the bottom layer is optimized for this number
blackhole.consume(randomGenerator.get().nextInt(1, 100));
}
public static void main(String[] args) throws RunnerException {
Options opt = new OptionsBuilder().include(TestRandomGenerator.class.getSimpleName()).build();
new Runner(opt).run();
}
}
Test results:
Benchmark (name) Mode Cnt Score Error Units TestRandomGenerator.testRandomInt Random thrpt 50 276250026.985 ± 240164319.588 ops/s TestRandomGenerator.testRandomInt SecureRandom thrpt 50 2362066.269 ± 1277699.965 ops/s TestRandomGenerator.testRandomInt SplittableRandom thrpt 50 365417656.247 ± 377568150.497 ops/s TestRandomGenerator.testRandomInt Xoroshiro128PlusPlus thrpt 50 341640250.941 ± 287261684.079 ops/s TestRandomGenerator.testRandomInt Xoshiro256PlusPlus thrpt 50 343279172.542 ± 247888916.092 ops/s TestRandomGenerator.testRandomInt L64X256MixRandom thrpt 50 317749688.838 ± 245196331.079 ops/s TestRandomGenerator.testRandomInt L64X128StarStarRandom thrpt 50 294727346.284 ± 283056025.396 ops/s TestRandomGenerator.testRandomInt L64X128MixRandom thrpt 50 314790625.909 ± 257860657.824 ops/s TestRandomGenerator.testRandomInt L64X1024MixRandom thrpt 50 315040504.948 ± 101354716.147 ops/s TestRandomGenerator.testRandomInt L32X64MixRandom thrpt 50 311507435.009 ± 315893651.601 ops/s TestRandomGenerator.testRandomInt L128X256MixRandom thrpt 50 187922591.311 ± 137220695.866 ops/s TestRandomGenerator.testRandomInt L128X128MixRandom thrpt 50 218433110.870 ± 164229361.010 ops/s TestRandomGenerator.testRandomInt L128X1024MixRandom thrpt 50 220855813.894 ± 47531327.692 ops/s TestRandomGenerator.testRandomIntWithBound Random thrpt 50 248088572.243 ± 206899706.862 ops/s TestRandomGenerator.testRandomIntWithBound SecureRandom thrpt 50 1926592.946 ± 2060477.065 ops/s TestRandomGenerator.testRandomIntWithBound SplittableRandom thrpt 50 334863388.450 ± 92778213.010 ops/s TestRandomGenerator.testRandomIntWithBound Xoroshiro128PlusPlus thrpt 50 252787781.866 ± 200544008.824 ops/s TestRandomGenerator.testRandomIntWithBound Xoshiro256PlusPlus thrpt 50 247673155.126 ± 164068511.968 ops/s TestRandomGenerator.testRandomIntWithBound L64X256MixRandom thrpt 50 273735605.410 ± 87195037.181 ops/s TestRandomGenerator.testRandomIntWithBound L64X128StarStarRandom thrpt 50 291151383.164 ± 192343348.429 ops/s TestRandomGenerator.testRandomIntWithBound L64X128MixRandom thrpt 50 217051928.549 ± 177462405.951 ops/s TestRandomGenerator.testRandomIntWithBound L64X1024MixRandom thrpt 50 222495366.798 ± 180718625.063 ops/s TestRandomGenerator.testRandomIntWithBound L32X64MixRandom thrpt 50 305716905.710 ± 51030948.739 ops/s TestRandomGenerator.testRandomIntWithBound L128X256MixRandom thrpt 50 174719656.589 ± 148285151.049 ops/s TestRandomGenerator.testRandomIntWithBound L128X128MixRandom thrpt 50 176431895.622 ± 143002504.266 ops/s TestRandomGenerator.testRandomIntWithBound L128X1024MixRandom thrpt 50 198282642.786 ± 24204852.619 ops/s
In the previous result verification, we have known that SplittableRandom has the best performance in single thread, and the best performance in multi-threaded environment is ThreadLocalRandom with similar algorithm but multi-threaded optimization
How to select random algorithm
The principle is to look at your business scenario, how many random combinations there are and within what range. Then find the best algorithm in the Period larger than this range. For example, the business scenario is a deck of poker. In addition to the big and small king 52 cards, the licensing order is determined by random numbers:
- First card: random generator Nextint (0, 52), choose from the remaining 52 cards
- Second card: random generator Nextint (0, 51), choose from the remaining 51 cards
- and so on
Then there are 52! So many results range from 2 ^ 225 to 2 ^ 226. If the Period of the random number generator we use is less than this result set, we may never generate the order of some cards. Therefore, we need to select a Period > 54! Random number generator.
Future outlook
Random number generator in project room
If there is no optimization for ThreadLocal in project room, the randomness performance of ThreadLocalRandom will also deteriorate, because virtual thread is an object like object that can be continuously generated and recycled, and ThreadLocalRandom cannot be enumerated indefinitely. At this time, we may need to use fixed multiple random number generators for all virtual threads instead of ThreadLocalRandom:
ExecutorService vte = Executors.newVirtualThreadExecutor();
SplittableGenerator source = RandomGeneratorFactory.<SplittableGenerator>of("L128X1024MixRandom").create();
//128 different random number generators are divided
List<RandomGenerator> rngs = source.splits(128);
AtomicInteger i = new AtomicInteger(0);
vte.submit(() -> {
long random = rngs.get(Math.abs(i.incrementAndGet() & 127)).nextLong();
...
});
Random number generator under the Scoped Local property
Scoped Local It is a more general domain variable (for example, ThreadLocal, that is, when the frontline process domain is local, Scoped Local can support different domains, including virtual thread, thread, method domain, package domain, etc.). At present, no version has been published to plan development. However, according to the current disclosure, we can better allocate random number generators to each thread in the following way:
private final static ScopeLocal<SplittableGenerator> rng_scope =
ScopeLocal.inheritableForType(SplittableGenerator.class);
public static void main(String[] args) throws InterruptedException {
SplittableGenerator rng1 =
RandomGeneratorFactory.<SplittableGenerator>of("L128X1024MixRandom").create();
SplittableGenerator rng2 =
RandomGeneratorFactory.<SplittableGenerator>of("L32X64MixRandom").create();
try (ExecutorService vte = Executors.newVirtualThreadExecutor()) {
for (int i = 0; i < 5; i++) {
ScopeLocal.where(rng_scope, rng1.split(), () -> { vte.submit(new Task()); });
}
for (int i = 0; i < 5; i++) {
ScopeLocal.where(rng_scope, rng2.split(), () -> { vte.submit(new Task()); });
}
}
}
private static class Task implements Runnable {
@Override public void run() {
SplittableGenerator rng = rng_scope.get();
System.out.println(rng);
}
}
WeChat search "my programming meow" attention to the official account, daily brush, easy to upgrade technology, and capture all kinds of offer:
