catalogue
2, Operation and implementation of binary search tree
2. Traversing binary search tree
5. Deletion of binary search tree
(2). The deleted node is a leaf node
(3). The deleted node has a child node
(4). The deleted node has two child nodes
3, Defects of binary search tree
1, Binary search tree
Binary Search Tree (BST), also known as binary sort tree or Binary Search Tree
Binary search tree is a binary tree and can be empty; If it is not empty, the following properties are met:
- All key values of non empty left subtree are less than those of its root node.
- All key values of non empty right subtree are greater than those of its root node.
- The left and right subtrees themselves are binary search trees.
For example, the first one in the following figure is not a binary search tree, and the second and third ones conform to the characteristics of a binary search tree
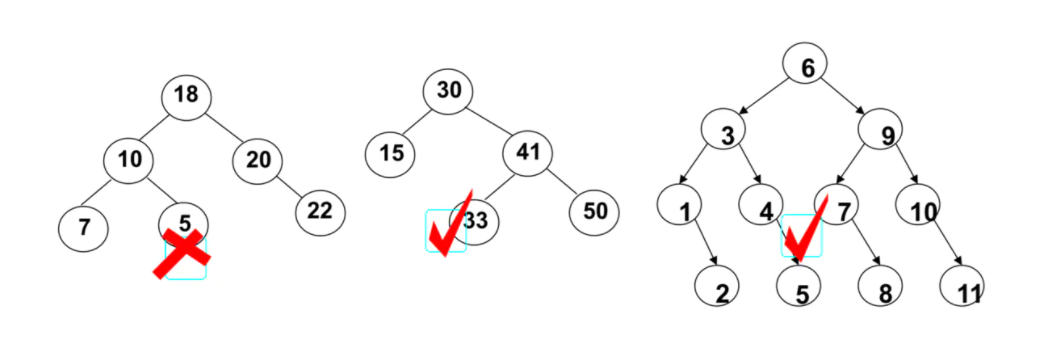
Features of binary search tree:
Relatively small values are always saved on the left node, and relatively large values are always saved on the right node. The search efficiency is very high, which is also the source of the word "search" in the binary search tree.
2, Operation and implementation of binary search tree
- insert(key): inserts a new key into the tree.
- search(key): find a key in the tree. If the node exists, return true; If it does not exist, false is returned.
- inOrderTraverse: traverse all nodes in the middle order traversal mode.
- preOrderTraverse: traverse all nodes through preorder traversal.
- postOrderTraverse: traverses all nodes by post order traversal.
- min: returns the smallest value / key in the tree.
- max: returns the largest value / key in the tree.
- remove(key): removes a key from the tree.
1. insert data
//Insert data: a method called externally to the user
BinarySerachTree.prototype.insert = function(key){
//1. Create a node according to the key
var newNode = new Node(key)
//2. Judge whether the root node has a value
if(this.root == null){
this.root = newNode
}else{
this.insertNode(this.root,newNode)
}
}
BinarySerachTree.prototype.insertNode = function(node,newNode){
if(newNode.key < node.key){//Find left
if(node.left == null){
node.left = newNode
}else{
this.insertNode(node.left,newNode)
}
}else{//Find right
if(node.right == null){
node.right = newNode
}else{
this.insertNode(node.right,newNode)
}
}
}2. Traversing binary search tree
The traversal of the tree here is applicable to all binary trees, not just binary search trees.
Traversal of tree:
Traversing a tree refers to accessing each node of the tree (you can also perform some operations on each node). There are three common ways to traverse binary trees: first order traversal, middle order traversal and subsequent traversal. (there is also program traversal, which is less used and can be completed by using queues)
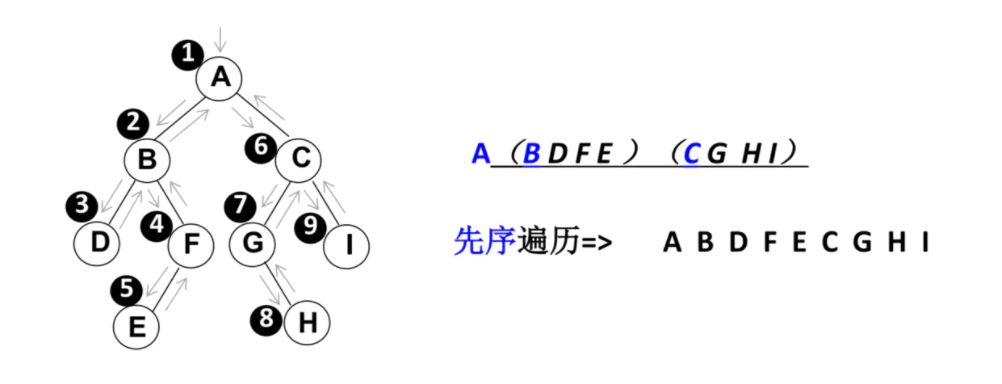
(1). Preorder traversal
The traversal process is:
- ① Access the root node;
- ② First, traverse its left subtree in order;
- ③ First traverse its right subtree.
Traversal process:
Code implementation:
//1. Preorder traversal
BinarySerachTree.prototype.preOrderTraversal = function (handler) {
this.preOrderTraversalNode(this.root, handler)
}
BinarySerachTree.prototype.preOrderTraversalNode = function (node, handler) {
if (node !== null) {
//1. Processed nodes
handler(node.key)
//2. Process the left child node of the passing node
this.preOrderTraversalNode(node.left, handler)
//3. Process the right child node of the passing node
this.preOrderTraversalNode(node.right, handler)
}
}Test code:
//Test code
var pkq = new BinarySerachTree()
pkq.insert(11)
pkq.insert(3)
pkq.insert(6)
pkq.insert(21)
pkq.insert(17)
pkq.insert(5)
//Test traversal
var resultString = ""
pkq.preOrderTraversal(function(key) {
resultString += key + " "
})
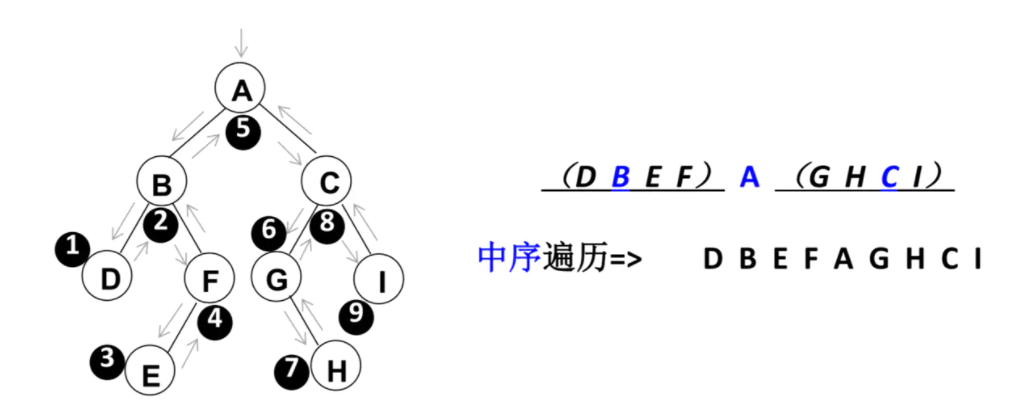
alert(resultString)(2). Medium order traversal
The traversal process is:
- ① Traversing its left subtree in middle order;
- ② Access the root node;
- ③ Traverse its right subtree in middle order.
Traversal process:
Code implementation:
//2. Middle order traversal
BinarySerachTree.prototype.midOrderTraversal = function(handler){
this.midOrderTraversalNode(this.root,handler)
}
BinarySerachTree.prototype.midOrderTraversalNode = function(node,handler){
if(node !== null){
//1. Process the nodes in the left subtree
this.midOrderTraversalNode(node.left,handler)
//2. Processing node
handler(node.key)
//3. Process the nodes in the right subtree
this.midOrderTraversalNode(node.right,handler)
}
}Test code:
//2. Middle order traversal
var resultString = ""
pkq.midOrderTraversal(function(key) {
resultString += key + " "
})
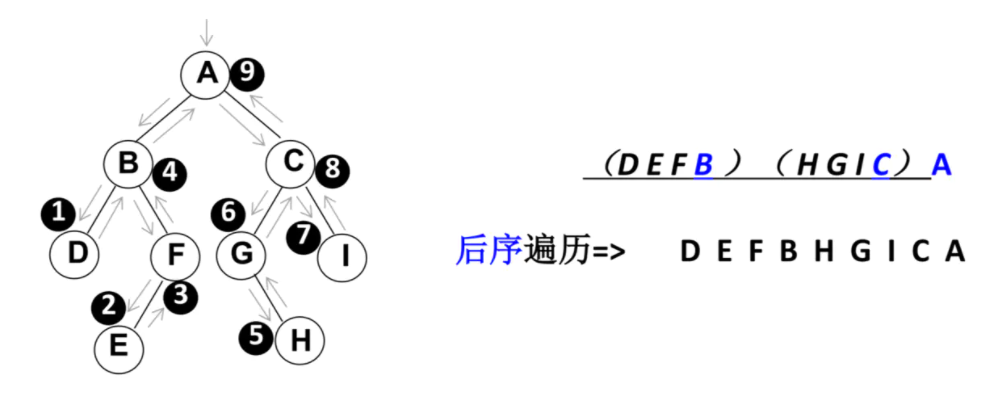
alert(resultString)(3). Postorder traversal
The traversal process is:
- ① After traversing its left subtree;
- ② After traversing its right subtree;
- ③ Access the root node.
Traversal process:
Code implementation:
//3. Post order traversal
BinarySerachTree.prototype.postOrderTraversal = function(handler){
this.postOrderTraversalNode(this.root,handler)
}
BinarySerachTree.prototype.postOrderTraversalNode = function(node,handler){
if(node !== null){
//1. Process the nodes in the left subtree
this.postOrderTraversalNode(node.left,handler)
//2. Process the nodes in the right subtree
this.postOrderTraversalNode(node.right,handler)
//3. Processing node
handler(node.key)
}
}Test code:
//3. Post order traversal
resultString = ""
pkq.postOrderTraversal(function(key) {
resultString += key + " "
})
alert(resultString)3. Maximum and minimum
Find the leftmost node to the left in turn is the minimum value, and the code finds the rightmost node to the right in turn is the maximum value.
//Find the best value
//1. Find the maximum value
BinarySerachTree.prototype.max = function(){
//1. Get root node
var node = this.root
//2. Keep searching to the right until the node is null
var key = null
while(node !== null){
key = node.key
node = node.right
}
return key
}
//2. Find the minimum value
BinarySerachTree.prototype.min = function(){
//1. Get root node
var node = this.root
//2. Keep looking to the left until the node is null
var key = null
while(node !== null){
key = node.key
node = node.left
}
return key
}4. Search for specific values
Binary search tree is very efficient in obtaining the most value and searching for a specific value. The following is implemented using recursive method and loop method respectively. On how to choose recursive method and loop method, in fact, recursion and loop can be converted to each other. In most cases, recursive calls can simplify the code, but also increase the complexity of space. The complexity of loop space is low, but the code will be relatively complex.
Recursive method:
//Search for specific values
BinarySerachTree.prototype.search = function (key) {
return this.searchNode(this.root, key)
}
BinarySerachTree.prototype.searchNode = function (node, key) {
//1. If the incoming node is null, exit recursion
if (node == null) {
return false
}
//2. Judge the value of the node node and the size of the passed in key
if (node.key > key) {//2.1. The passed in key is small. Continue to search to the left
return this.searchNode(node.left, key)
} else if (node.key < key) {//2.2. The key passed in is large. Continue to search to the right
return this.searchNode(node.right, key)
} else {//2.3. Same, indicating that the key is found
return true
}
}Circulation method:
//Search for a specific value and complete it with a for loop
BinarySerachTree.prototype.search = function(key){
//1. Get the root node
var node = this.root
//2. Circular search key
while(node !== null){
if(key < node.key){
node = node.left
}else if(key > node.key){
node = node.right
}else{
return true
}
}
return false
}5. Deletion of binary search tree
To delete a node, you need to find the node first. There are three cases:
1. This node is a leaf node
2. This node has a child node
3. This node has two child nodes
(1). Find the node to delete
BinarySerachTree.prototype.remove = function(key){
//1. Find the node to delete
//1.1. Define variables and save some information
var current = this.root
var parent = null
var isLeftChild = true
//1.2. Start looking for deleted nodes
while(current.key != key){
parent = current
if(key<current.key){
isLeftChild = true
current = current.left
}else{
isLeftChild = false
current = current.right
}
//A certain situation: the last node has been found, but = = key is still not found
if(current == null) return false
}
(2). The deleted node is a leaf node
//2.1. The deleted node is a leaf node (no child nodes)
if(current.left == null && current.right == null){
if(current == this.root){
this.root = null
}else if(isLeftChild){
parent.left = null
}else{
parent.right = null
}
}(3). The deleted node has a child node
//2.2. The deleted node has a child node
else if(current.right == null){
if(current == this.root){
this.root = current.left
}else if(isLeftChild){
parent.left = current.left
}else{
parent.right = current.left
}
}else if(current.left == null){
if(current == this.root){
this.root = current.right
}else if(isLeftChild){
parent.left = current.right
}else{
parent.right = current.right
}
}
(4). The deleted node has two child nodes
Delete a rule with two nodes:
If the node to be deleted has two child nodes, even the child node has child nodes, in this case, you need to find a node from the following child nodes to replace the current node.
The node to be found should be the closest to the current node among all the nodes under the current node. It is either a little smaller than the current node or a little larger than the current node.
A node smaller than current must be the maximum value of the left subtree of current; A node a little larger than current must be the minimum value of the right subtree of current.
In the binary search tree, these two special nodes have two special names: predecessor and successor. Nodes smaller than current are called precursors of current nodes; A node a little larger than current is called the successor of current node.
Therefore, find such a node (precursor or successor) first
Look for subsequent code implementations:
//Find a successor
BinarySerachTree.prototype.getSuccssor = function (delNode) {
//1. Define variables and save the found successors
var successor = delNode
var current = delNode.right
var successorParent = delNode
//2. Circular search
while (current != null) {
successorParent = successor
successor = current
current = current.left
}
//3. Judge whether the sought successor node is directly the right node of delNode
if (successor != delNode.right) {
successorParent.left = successor.right
successor.right = delNode.right
}
return successor
}Delete a code with two child nodes:
//2.3. The deleted node has two child nodes
else {
// 1. Obtain subsequent nodes
var successor = this.getSuccessor(current)
// 2. Judge whether it is the root node
if (current == this.root) {
this.root = successor
} else if (isLeftChild) {
parent.left = successor
} else {
parent.right = successor
}
// 3. Assign the left subtree of the deleted node to success
successor.left = current.left
}3, Defects of binary search tree
Binary search tree can quickly find data items with given keywords, and can quickly insert and delete data items, but it has a defect. For example, when inserting 7, 6, 5, 4 and 3 into a binary tree initialized to 9, 8 and 12, it will cause uneven distribution.
Better binary search tree data should be evenly distributed on the left and right, and unevenly distributed trees are called unbalanced trees. For a balanced binary tree, the search and insertion efficiency is O(logN). For an unbalanced binary tree, it is equivalent to a linked list, and the search efficiency becomes O(N)
The common balanced trees are AVL tree and red black tree