sort

Sorting is an algorithm that arranges data in a certain order. The following are introduced one by one.

1, Bubble sorting

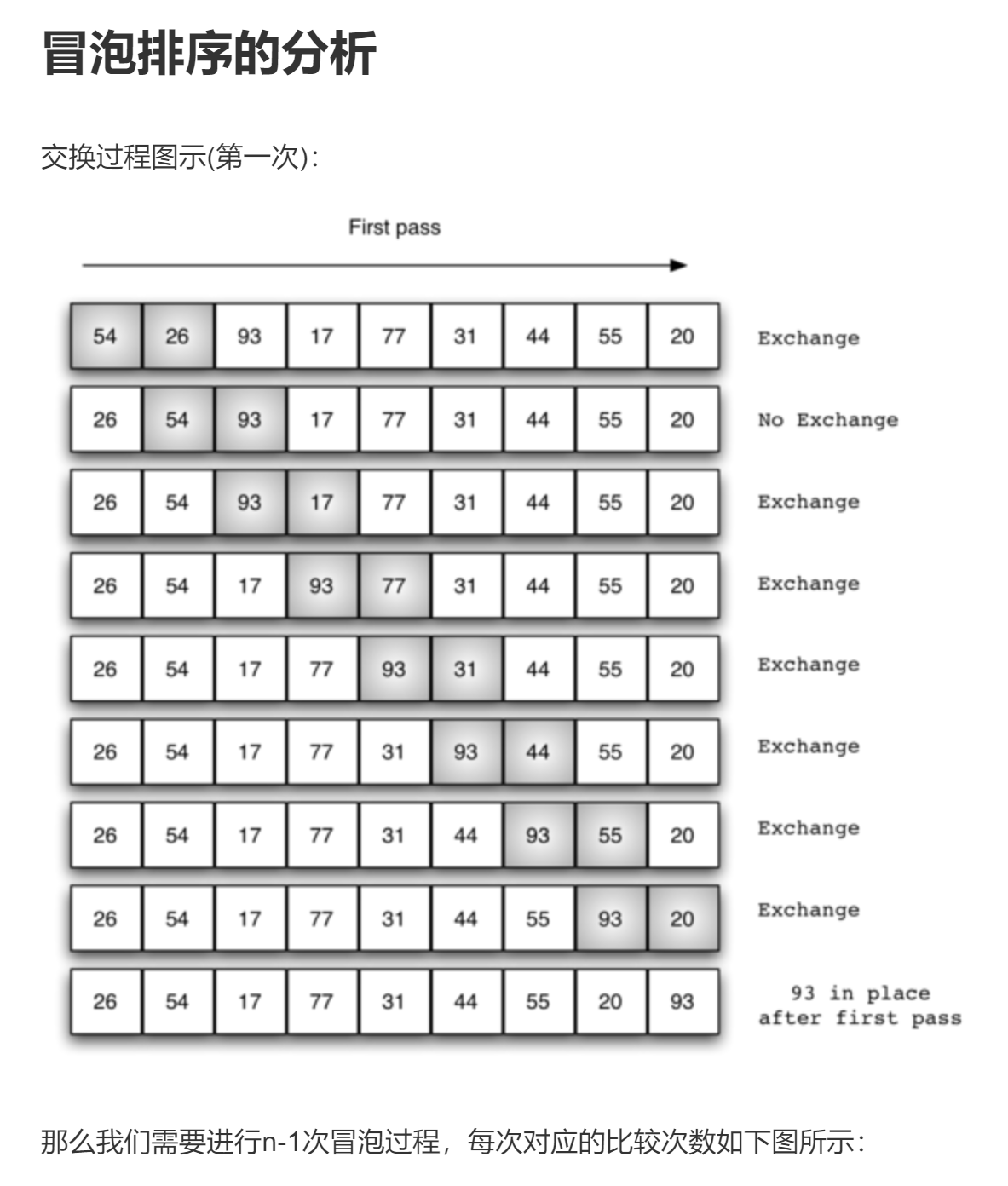
Bubble sorting is to compare the elements between lists in pairs, and the large exchange position is to the right. In the first pairwise comparison, the largest element must be placed on the far right, so the second traversal only needs to traverse n-1 times.

def bubble_sort(urlist):
	#Number of iterations required
    for j in range(len(urlist) - 1, 0, -1):
    	#Compare each other
        for i in range(j):
            if urlist[i] > urlist[i + 1]:
            	#Exchange positions with intermediate variables
                m = urlist[i + 1]
                urlist[i + 1] = urlist[i]
                urlist[i] = m
    print(urlist)


li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
bubble_sort(li)

2, Select sort

The main idea of selective sorting is to first find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence, and then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
The main advantage of selective sorting is related to data movement. If an element is in the correct final position, it will not be moved. Select sort to exchange a pair of elements each time, and at least one of them will be moved to its final position. Therefore, sort the table of n elements and exchange at most n-1 times in total. Among all the sorting methods that completely rely on exchange to move elements, selective sorting is a very good one.

# 1. Select the smallest value in the list and place it on the smallest index
def choose_sort(urlist):
    n = len(urlist)
    for i in range(n - 1):  # The number of times to cycle, the smallest element does not have to be recycled after it is located
        min_index = i  # Determine minimum location index
        for j in range(i, n):  # Traverse from the minimum position to the end of the table
            if urlist[j] < urlist[min_index]:
                min_index = j
        if min_index != i:
            m = urlist[min_index]
            urlist[min_index] = urlist[i]
            urlist[i] = m
    print(urlist)


urlist = [54, 226, 93, 17, 77, 31, 44, 55, 20]
choose_sort(urlist)

# 2. Select the largest value in the list and place it on the largest index
def big_sort(alist):
    n = len(alist)
    for i in range(n - 1, 0, -1):  # Traverse from footer to header
        max_index = i  # Determine the rightmost position
        for j in range(i, -1, -1):  # Traverse from the rightmost position to the left
            if alist[j] > alist[max_index]:  # Find maximum
                max_index = j
        if max_index != i:
            alist[i], alist[max_index] = alist[max_index], alist[i]  # change of position
    print(alist)


urlist = [54, 226, 93, 17, 77, 31, 44, 55, 20]
big_sort(urlist)

3, Insert sort

Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it. In the implementation of insertion sorting, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements back step by step to provide insertion space for the latest elements.

# Insert sort
# Start from the second position in the list and compare one by one. If the conditions are met, change the position.
def insert_sort(alist):
    n=len(alist)
    for i in range(1,n):
        for j in range(i,0,-1):# Compared with the previous position, there is j-1 behind it, so the position 0 does not have to contain
            if alist[j]<alist[j-1]:
                alist[j],alist[j-1]=alist[j-1],alist[j] #Exchange position
    print(alist)
urlist = [54, 226, 93, 17, 77, 31, 44, 55, 20]
insert_sort(urlist)

4, Quick sort

Through one-time sorting, the data to be sorted is divided into two independent parts. All data in one part is smaller than all data in the other part, and then the two parts of data are sorted quickly according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.
The steps are:

1. Select an element from the sequence, which is called "pivot",
2. Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition, the benchmark is in the middle of the sequence. This is called a partition operation.
3. Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element.
The bottom case of recursion is that the size of the sequence is zero or one, that is, it has always been sorted. Although it recurses all the time, the algorithm will always end, because in each iteration, it will put at least one element to its last position.

# Quick sort
def quick_sort(alist, start, end):
    """Quick sort"""
    # Recursive derivation condition
    if start >= end:
        return
    # Set the starting element as the base element to find the position
    mid = alist[start]
    # low is the cursor moving from left to right on the left of the sequence
    low = start
    # high is the cursor moving from right to left on the right side of the sequence
    high = end
    while low < high:
        # If low does not coincide with high, and the element pointed by high is not smaller than the reference element, high moves to the left
        while low < high and alist[high] >= mid:
            high -= 1
        alist[low] = alist[high]
        # If low does not coincide with high, and the element pointed to by low is smaller than the base element, low moves to the right
        while low < high and alist[low] < mid:
            low += 1
        alist[high] = alist[low]

    alist[low] = mid
    # Quick sort the subsequence to the left of the base element
    quick_sort(alist, start, low - 1)
    # Quick sort the subsequence to the right of the base element
    quick_sort(alist, low + 1, end)


alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
quick_sort(alist, 0, len(alist) - 1)
print(alist)