Binary tree recursion routine: judge whether the binary tree is a complete binary tree and whether the binary tree is a balanced binary tree

Posted by hip_hop_x on Mon, 17 Jan 2022 18:02:57 +0100

We are already familiar with the basic routine of binary tree. Next, let's talk about the recursive routine of binary tree, which can solve most binary tree problems in the interview, especially the tree dp problem. Its essence is to use the convenience of recursion to traverse binary tree.

Judge whether the binary tree is a complete binary tree

1. Classical writing ideas

(1) If a node has right children but no left children, it must not be a complete binary tree

(2) When a node with incomplete left and right children is encountered for the first time, the nodes encountered later are leaf nodes

2. Recursive routine idea

For any subtree, the conditions for judging whether it is a complete binary tree (list all possibilities)

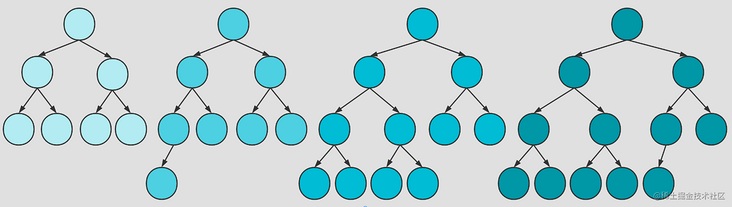
(1) The left tree is full, the right tree is full, and the left tree height = the right tree height

(2) The left tree is a complete binary tree, the right tree is full, and the left tree height = the right tree height + 1

(3) Left tree is full, right tree is full, left tree height = right tree height + 1

(4) The left tree is full, the right tree is a complete binary tree, and the left tree height = the right tree height

Only in these four cases can a binary tree be a complete binary tree (of course, it may also be a full binary tree, and the full binary tree itself is also a complete binary tree)

That is, each time from the left subtree and the right subtree, we need three data: full binary tree, complete binary tree and height. Although we only return whether it is complete binary tree, we need height and full to help us judge whether it is complete binary tree, so we can define the following Info class

public static class Info {
    public boolean isFull;
    public boolean isComplete;
    public int height;

    public Info(boolean isFull, boolean isComplete, int height) {
        this.isFull = isFull;
        this.isComplete = isComplete;
        this.height = height;
    }
}

3. Recursive routine code

(1) First, judge whether it is good to set when the node is empty. When the node is empty, new Info(true, true, 0), that is, it is considered that the empty node is a full binary tree, a complete binary tree and a height of 0.

(2) Then, according to all the possibilities listed, write the code of the recursive routine. Because the whole recursion should be formed, the Info class should be returned at each step. Otherwise, how can we recurse?

The core routine of this step is the following three steps:

1) No brain obtains the Info information of the left and right subtrees

2) Put together your own Info information according to the left and right subtrees

3) Return your own Info information

/**
 * @author Java And algorithm learning: Monday
 */
public static Info process(Node x) {
    if (x == null) {
        return new Info(true, true, 0);
    }

    //Get left and right subtrees
    Info leftInfo = process(x.left);
    Info rightInfo = process(x.right);

    //Piece together your own information
    boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
    boolean isComplete = false;
    if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
        //Left full, right full, equal height
        isComplete = true;
    } else if (leftInfo.isComplete && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
        //Left full, right full, height difference 1
        isComplete = true;
    } else if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
        //Left full, right full, height difference is 1
        isComplete = true;
    } else if (leftInfo.isFull && rightInfo.isComplete && leftInfo.height == rightInfo.height) {
        //The left is full and the right is complete, and the height is equal
        isComplete = true;
    }
    //The maximum height of the left and right subtrees plus their own height 1 is the height of this node
    int height = Math.max(leftInfo.height, rightInfo.height) + 1;

    return new Info(isFull, isComplete, height);
}

(3) The main function calls the recursive method to get the result

/**
 * Recursive routine method
 *
 * @author Java And algorithm learning: Monday
 */
public static boolean isCompleteBinaryTree2(Node head) {
    if (head == null) {
        return true;
    }
    return process(head).isComplete;
}

All code addresses:

https://github.com/monday-pro...

Judge whether the binary tree is a balanced binary tree

Definition of balanced binary tree: in each subtree of a binary tree, the difference between the maximum height of the left tree and the maximum height of the right tree is less than or equal to 1.

1. Recursive routine idea

Analyze the condition that the subtree with this node as the head is a balanced binary tree for any node (list all possibilities)

(1) The left tree is a balanced binary tree

(2) The right tree is a balanced binary tree

(3) The difference between the left tree height and the right tree height is less than or equal to 1

Only when these three conditions are satisfied can we say that the subtree with this node as the head is a balanced binary tree.

That is, we need the data of balance and height from the left subtree and the right subtree every time. Although we only return whether it is balanced, we need height to help us judge whether it is balanced. Therefore, we can define the following Info class

public static class Info{
    public boolean isBalanced;
    public int height;

    public Info(boolean b, int h) {
        this.isBalanced = b;
        this.height = h;
    }
}

2. Recursive routine code

(1) First, judge whether it is good to set when the node is empty. When the node is empty, new Info(true, 0), that is, it is considered that the empty node is a balanced binary tree with a height of 0.

(2) Then write the code of the recursive routine according to all the possibilities listed. Because the whole recursion is to be formed, the Info class must be returned at each step. (get the Info of the left and right subtrees, piece together your own Info, and return your own Info)

/**
 * Judge whether the subtree headed by a node is a balanced binary tree
 *
 * @author Java And algorithm learning: Monday
 */
public static Info process(Node x) {
    if (x == null) {
        return new Info(true, 0);
    }

    // 1. Get the information of the left and right subtrees
    Info leftInfo = process(x.left);
    Info rightInfo = process(x.right);

    // 2. Piece together my own information
    //The default is balanced
    boolean isBalanced = true;
    //What will cause imbalance: 1 Left tree imbalance 2 Right tree imbalance 3 The height difference between the left and right subtrees is greater than 1
    if (!leftInfo.isBalanced || !rightInfo.isBalanced || Math.abs(leftInfo.height - rightInfo.height) > 1) {
        isBalanced = false;
    }
    //The maximum height of the left and right subtrees, plus their own height
    int height = Math.max(leftInfo.height, rightInfo.height) + 1;

    // 3. Return your own information
    return new Info(isBalanced, height);
}