Nanchang Institute of technology acm summer training
This week I learned the hash table in the data structure and practiced some data structure topics I learned last week
Next week, the multi school league will start to learn search and graph theory while making supplementary questions for the competition
General hash table
Definition of hash table: hash table is a data mapping structure that looks for values according to key codes. This structure looks for the place where values are stored by mapping the key codes
Hash table, also known as hash table, is generally implemented by hash function (hash function) and linked list structure. Similar to the idea of discretization, when we want to make statistics on some complex information, we can use hash function to map these complex information into a value domain that is easy to maintain.
Hash Collisions
As the definition says, hash is to find the location of stored values through key mapping. Because the value range becomes simpler and the range becomes smaller, it may cause two different original information to be mapped to the same value by the hash function, so we need to deal with this conflict.
For example, different storage values are mapped to the same address
The stored values are: 3, 6, 9. The p value is 3
Then 3 mod 3 == 6 mod 3 == 9 mod 3.
So there was a conflict between 3, 6 and 9
Hash conflict resolution
Zipper method and open addressing method are commonly used
1. Zipper method
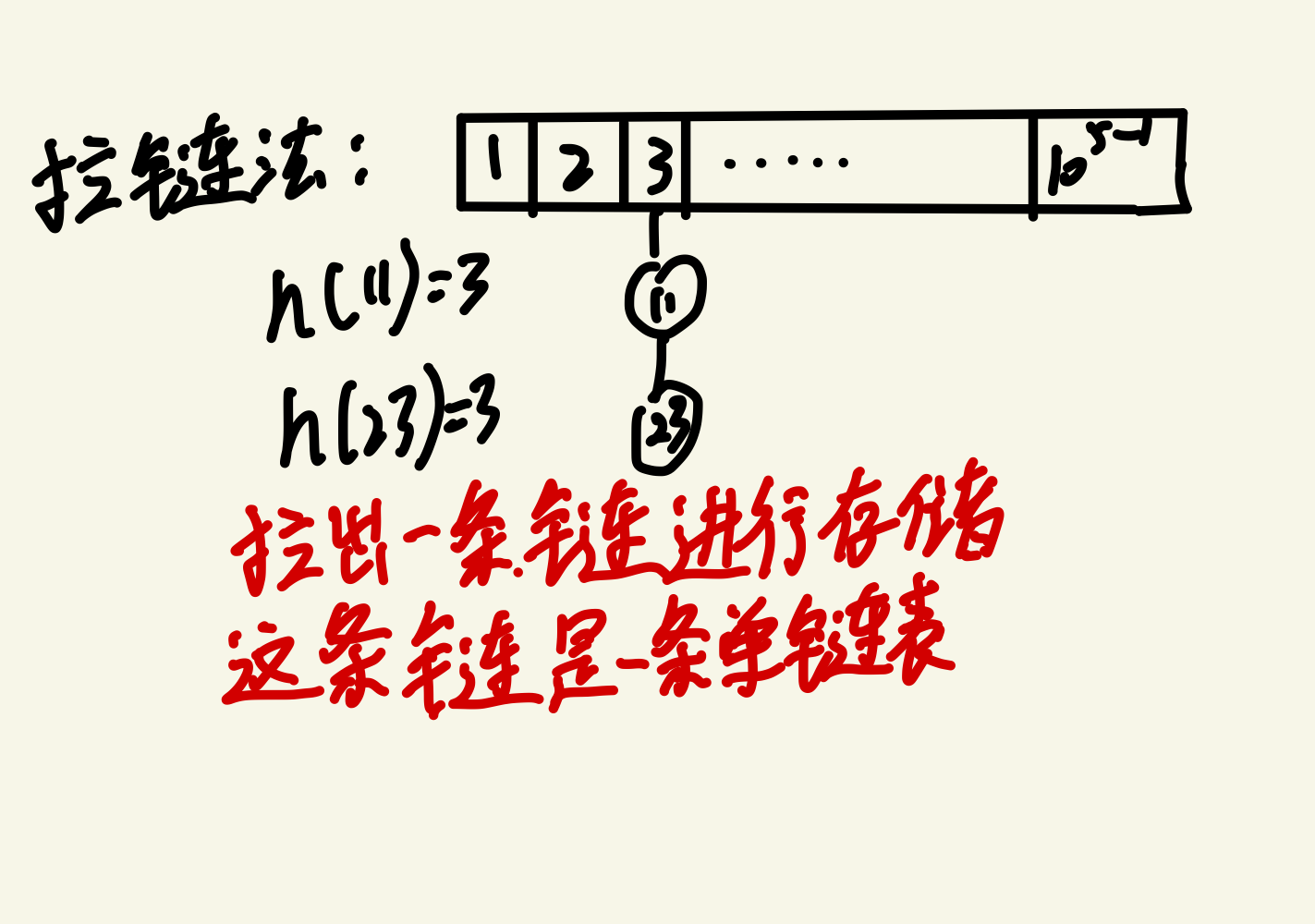
The zipper method pulls out a single linked list at the conflicting position to store the conflicting values
be careful:
When finding the remainder, when taking the module, it should be a prime number and as far away from the integer power of 2 as possible. The conflict caused by this is the smallest
Template for zipper method:
int h[N], e[N], ne[N], idx;
// Inserts a number into the hash table
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// Query whether a number exists in the hash table
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
2. Open addressing method

The open addressing method is the same as going to the toilet. Start from the K-th pit until you find an empty position, and then go in.
Template:
int h[N];
// If x is in the hash table, the subscript of X is returned; If x is not in the hash table, the position where x should be inserted is returned
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
Find the first mock exam question in two ways: acwing simulation scattered list
Zipper method:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+3;//When finding the remainder, when taking the module, it should be a prime number and as far away from the integer power of 2 as possible. The conflict caused by this is the smallest
int h[N],e[N],ne[N],idex;//h[N] is the slot of the hash table, e[N] is the stored value, en{N] is the next pointer in the single linked list, and the current position reached by idex
void insert(int x)
{
int k=(x%N+N)%N;//In c + +, if x is positive, it will be positive after modulo n, and if x is negative, it will be negative after modulo n+ N%N guarantees that the final value must be positive k is the hash value, and the value is mapped between 1 and n
//These three steps are the same as the single linked list insertion method
e[idex]=x;
ne[idex]=h[k];
h[k]=idex++;
}
bool find(int x)
{
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i])
{
if(e[i]==x) return true;
}
return false;
}
int main()
{
int n;
cin>>n;
memset(h,-1,sizeof(h));//Empty the tank
while(n--)
{
char p;
int x;
cin>>p>>x;
if(p=='I')
insert(x);
else
{
if(find(x)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
}
Open addressing:
#include<bits/stdc++.h>
using namespace std;
//The open addressing method is generally 2 ~ 3 times the data range, so there is no conflict in the probability
const int N = 2e5 + 3; //The first prime number greater than the data range
const int null = 0x3f3f3f3f; //Null pointer specified 0x3f3f3f
int h[N];
int find(int x) {
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x) {
t++;
if (t == N) {
t = 0;
}
}
return t; //If this location is empty, it returns the location it should store
}
int n;
int main() {
cin >> n;
memset(h, 0x3f, sizeof h); //Null pointer specified as 0x3f3f3f3f
while (n--) {
string op;
int x;
cin >> op >> x;
if (op == "I") {
h[find(x)] = x;
} else {
if (h[find(x)] == null) {
puts("No");
} else {
puts("Yes");
}
}
}
return 0;
}
String hash
String hashing is essentially converting each different string into a different integer. And ensure that different strings get different hash values, which can be used to judge whether the string has been repeated.
Formula method: Hash[i] = Hash[i-1]*p+idx(si)
be careful:
- Any character cannot be mapped to 0, otherwise different strings will be mapped to 0. For example, a, AA and AAA are all 0
- Conflict problem: by skillfully setting the values of P (131 or 13331) and Q (264) (264), it can generally be understood that there is no conflict.
The problem is to compare whether the substrings in different intervals are the same, which is transformed into whether the corresponding hash values are the same. Finding the hash value of a string is equivalent to finding the prefix sum, and finding the hash value of a string's substring is equivalent to finding the partial sum.
Prefix and formula h [i + 1] = h [i] × P+s[i]h[i+1]=h[i] × P+s[i] i ∈ [0,n − 1]i ∈ [0,n − 1] h is the prefix and array, and S is the string array
Interval sum formula h [l, R] = h [R] − h [l − 1] × Pr−l+1h[l,r]=h[r]−h[l−1] × Pr−l+1
Understanding of interval and formula: the first three character values of ABCDE and ABC are the same, with only two digits difference. Multiply by the quadratic power of P to change ABC into ABC00, and then ABCDE-ABC00 to obtain the hash value of DE.
Template:
Core idea: regard string as P Hexadecimal number, P The empirical value of is 131 or 13331, and the conflict probability of taking these two values is low
Tip: use 2 for modulo numbers^64,Use it directly unsigned long long The result of overflow is the result of modulo
typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k] stores the hash value of the first k letters of the string, and p[k] stores P^k mod 2^64
// initialization
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// Calculate the hash value of substring str[l ~ r]
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
Template questions: acwing string hash
Solution:
#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+5,P = 131;//13331,P = 131 or 13331,Q=2^64, there will be no conflict in 99% of the cases
ULL h[N],p[N];// h[i] hash value of the first I characters
// The string becomes a p-ary number, which reflects the character + order. It is necessary to ensure that different strings correspond to different numbers
ULL query(int l,int r){
return h[r] - h[l-1]*p[r-l+1];
}
int main(){
int n,m;
cin>>n>>m;
string x;
cin>>x;
p[0] = 1;//The string is numbered from 1, and h[1] is the hash value of the previous character
h[0] = 0;
for(int i=0;i<n;i++){
p[i+1] = p[i]*P;
h[i+1] = h[i]*P +x[i];//Prefix sum hash the entire string
}
while(m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
if(query(l1,r1) == query(l2,r2)) printf("Yes\n");
else printf("No\n");
}
return 0;
}
Finally, show me two more questions that feel OK this week
1.Luogu P1160 queue arrangement
Idea:
Although this topic is called queue arrangement, because n is still relatively large and constantly inserted and deleted, we can also use a linked list. When reading each student, update the students on his left and right; When deleting a classmate, first assign the classmate to 0, and then connect the classmate on his left to the classmate on his right; Finally, find the students on the left and output them one by one. Time complexity O(n).
(the idea is based on the "night sword God ten incense" of the big man of Luogu)
Solution: (analog linked list)
#include<cstdio>
#include<cstring>
int a[100010][3],n,m;
//a[i][2] indicates the student number of the student on the right of the student with student number I
//a[i][3] indicates the student number of the student on the left of the student with student number I
int main()
{
scanf("%d",&n); int j=1;
memset(a,0,sizeof(a)); a[1][1]=1;
for(int i=2;i<=n;i++)
{
int x,y; scanf("%d %d",&x,&y);
a[i][1]=i;
if(y==0)//Insert left
{
a[a[x][3]][2]=i; a[i][2]=x;
a[i][3]=a[x][3]; a[x][3]=i;
if(x==j) j=i;
}
else//Insert right
{
a[i][2]=a[x][2]; a[a[x][2]][3]=i;
a[x][2]=i; a[i][3]=x;
}
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int x; scanf("%d",&x);
if(a[x][1]!=0)//Classmate existence
{
a[x][1]=0;//Kick out
a[a[x][3]][2]=a[x][2];
a[a[x][2]][3]=a[x][3];
n--;
if(x==j) j=a[x][3];
}
}
int i=1,x=j;
while(i<=n)
{
printf("%d ",a[x][1]);
x=a[x][2]; i++;
}
return 0;
}
P4387 [Shenji 15. Xi 9] verification stack sequence
This question is a common operation of stacking in and out. Give two groups of data. The first group is the stacking order. Ask whether you can get the stacking order of the two groups according to the stacking order of the first group
Solution: (array simulation stack)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int stk[N],a[N],b[N],tt=-1,t,n;
int main()
{
cin>>t;
while(t--)
{
tt=-1;
cin>>n;
int f=1;
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=0;i<n;i++)
cin>>b[i];
int j=0;
for(int i=0;i<n;i++)
{
stk[++tt]=a[i];
while(stk[tt]==b[j])//When the top element of the stack is the same as the current element in b, the stack is released
{
tt--;
j++;
if(tt==-1) break;//Note here that when the stack is empty, the loop should be ended manually
}
}
if(tt==-1) cout<<"Yes"<<endl;//If the stack is empty, the stack sequence b is correct
else cout<<"No"<<endl;
}
}
OK, thanks for reading here