I Analysis and application of point divide and conquer principle



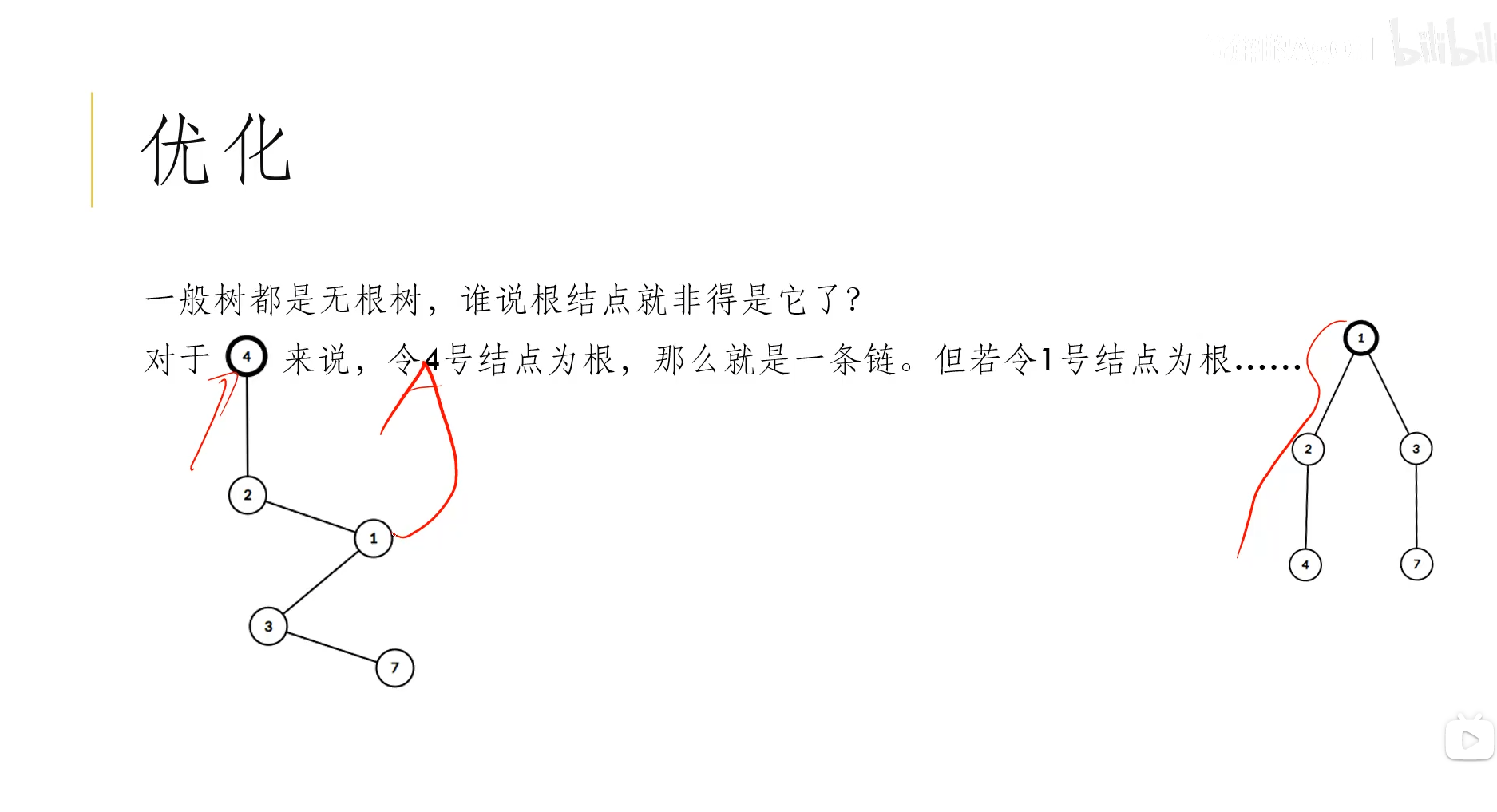





II Point divide and conquer Video Explanation
Video link
https://www.bilibili.com/video/BV1PE41197md?p=1
III Dot divide and conquer exercise
1.P3806 [template] point divide and conquer 1
1.P3806 [template] point divide and conquer 1
Analysis: the paths of two points are divided into two types: passing through the root node and not passing through the root node. Then we can use the point divide and conquer algorithm to process each point as the root once, calculate the distance from all nodes of the subtree with this node as the root to the root node, and then mark it with an array to calculate whether there is a point to point distance of k
AC Code:
#include<bits/stdc++.h>
using namespace std;
const int Maxn = 1e4+10;
const int Maxk = 1e8+10;
struct Edge{
int v;
int next;
int w;
}edge[Maxn*2];
int head[Maxn];
int cnt;
void build(int u,int v,int w){
edge[++cnt].v = v;
edge[cnt].w = w;
edge[cnt].next = head[u];
head[u] = cnt;
edge[++cnt].v = u;
edge[cnt].w = w;
edge[cnt].next = head[v];
head[v] = cnt;
return ;
}
//rt records the center of gravity, sum records the size of the current tree, and tot is the counter
int n,m,rt,sum,tot;
int siz[Maxn];
int dep[Maxn];
int tmp[Maxn];//Storage distance
int maxp[Maxn];//maxp stores the center of gravity of the tree
int Q[Maxn];//Storage query
//judge records whether the distance exists, the answer asked by ans, and whether the vis marked point is deleted
bool judge[Maxk],ans[105],vis[Maxn];
int dis[Maxn];
//Find the center of gravity, which is a little similar to tree chain sectioning
void getrt(int u,int f){
siz[u] = 1,maxp[u] = 0;//Maxp is initialized to 0, and maxp is used to find the center of gravity
//Traverse all the sons of u and find the size of the heavy son maxp
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
//If v is the parent node of u or the v node has been deleted, continue
if(v==f||vis[v]) continue;
getrt(v,u);
siz[u]+=siz[v];
//Renew your son
if(siz[v]>maxp[u]){
maxp[u] = siz[v];
}
}
//Then compare the size of the heavy son with the parent node of u
maxp[u] = max(maxp[u],sum-maxp[u]);
//Update Center of gravity
if(maxp[u]<maxp[rt]){
rt = u;//maxp[rt] has also been updated
}
return ;
}
void getdis(int u,int f){
/*The path length from all child nodes of the tree with u as the root to u*/
tmp[++tot] = dis[u];//First v-u save in
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
dis[v]=dis[u]+edge[i].w;
getdis(v,u);
}
return ;
}
void solve(int u){
static queue<int>q;
for(int i=head[u];i!=-1;i=edge[i].next){
tot = 0;
int v = edge[i].v;
if(vis[v]) continue;//Points that have been deleted
dis[v] = edge[i].w;
getdis(v,u);
for(int j=1;j<=tot;j++)//Traverse all distances
for(int k=1;k<=m;k++){//Traverse all queries
if(Q[k]>=tmp[j]) ans[k]|=judge[Q[k]-tmp[j]];
}
for(int j=1;j<=tot;j++){
q.push(tmp[j]);
judge[tmp[j]] = true;//Set to true to indicate that the distance exists
}
}
/*Initialize the tmp array distance to false to prevent affecting the judgment of the next subtree*/
while(!q.empty()){
judge[q.front()] = false;
q.pop();
}
}
//Divide and conquer
void divide(int u){
/*Delete the root (center of gravity) node, and judge[0]=true
Because the distance from the point to itself is 0*/
vis[u]=judge[0] = true;
solve(u);//Calculates the path through the root node
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
/*If the node has been deleted (including the parent node, which is processed from top to bottom), skip*/
if(vis[v]) continue;
maxp[rt=0]=sum=siz[v];//At this time, we should take the subtree with v node as the root as the research object
getrt(v,0);//Find the center of gravity of v
getrt(rt,0);//New siz array with barycenter as root
divide(rt);//Divide and conquer this subtree
}
}
void init(){
memset(vis,false,sizeof(vis));
memset(head,-1,sizeof(head));
return ;
}
int main()
{
init();
cin>>n>>m;
for(int i=1;i<n;i++){
int u,v,w;
cin>>u>>v>>w;
build(u,v,w);
}
for(int i=1;i<=m;i++) cin>>Q[i];
//There is no center of gravity at first, so it is rt=0 and set to the maximum value
maxp[0]=sum=n;
getrt(1,0);//Find the center of gravity
/*!At this time, the siz array stores the subtree size with 1 as the root,
You need to find a recalculation based on the center of gravity*/
getrt(rt,0);
divide(rt);//After finding the center of gravity, you can start divide and conquer and solve the answer
//cout<<"11\n";
for(int i=1;i<=m;i++){
if(ans[i]) cout<<"AYE\n";
else cout<<"NAY\n";
}
return 0;
}
2.P2634 [national training team
2.P2634 [national training team] Congcong cocoa
Analysis: this problem is mainly to calculate how many point pairs (you and yourself are also a pair). The sum of edge weights on the path is a multiple of 3 (note that 0 is also a multiple of 3). Obviously, this problem first converts the edge weight into point weight, and then uses point divide and conquer to treat each node as the root once. For each subtree with this node as the root node, Calculate the distance from all nodes to the root node. Obviously, we need to calculate the number of paths that are multiples of 3. If the array stores the path length, it will definitely MLE, so we might as well set the distance% 3 and then calculate the number of point pairs whose distance% 3 is 0. In this way, we only need to open 3 spaces for the array, which greatly saves space
AC Code:
/*Point divide and conquer*/
#include<bits/stdc++.h>
using namespace std;
const int Maxn = 2e4+10;
struct E{
int v;
int w;
int next;
}edge[Maxn*2];
int head[Maxn];
int n;
int maxp[Maxn];
int siz[Maxn];
bool vis[Maxn];
int dis[Maxn];
int tmp[Maxn];
int ans = 0;
int all = 0;
int cnt = 0;
int tot = 0;
int judge[3]={0};//Record the number of distances. Here is the distance after% 3
int sum = 0;
int rt;
/*Chain forward star*/
void build(int u,int v,int w){
edge[++cnt].v = v;
edge[cnt].w = w ;
edge[cnt].next = head[u];
head[u] = cnt;
edge[++cnt].v = u;
edge[cnt].w = w;
edge[cnt].next = head[v];
head[v] = cnt;
return ;
}
/*Record distance*/
void getdis(int u,int f){
tmp[++tot] = dis[u];
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
dis[v] = dis[u]+edge[i].w;
getdis(v,u);
}
return ;
}
/*Find the center of gravity of the tree and calculate the size*/
void getrt(int u,int f){
maxp[u] = 0;
siz[u] = 1;
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
//If v is the parent node of u or v and are deleted
if(v==f||vis[v]) continue;
getrt(v,u);//Update siz[v]
siz[u]+=siz[v];
if(siz[v]>maxp[u]){
maxp[u] = siz[v];
}
}
maxp[u] = max(maxp[u],sum-maxp[u]);
if(maxp[u]<=maxp[rt]){
rt = u;
}
return ;
}
void solve(int u){
for(int i=head[u];i!=-1;i=edge[i].next){
tot = 0;
int v = edge[i].v;
if(vis[v]) continue;//And deleted
dis[v] = edge[i].w;
getdis(v,u);
for(int i=1;i<=tot;i++){
int len = tmp[i]%3;
if(len==0) ans++;
int need = (3-len)%3;//Needed
ans+=judge[need];
}
/*It cannot be put into the for loop above, because the on a chain cannot be recalculated*/
for(int i=1;i<=tot;i++){
int len = tmp[i]%3;
judge[len]++;
}
}
for(int i=0;i<3;i++) judge[i] = 0;
return ;
}
/*Point divide and conquer processing node answer*/
void divide(int u,int f){
vis[u] = true;//vis[u]=1 means deleted
solve(u);//Calculate the path through the u node
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(vis[v]) continue;
maxp[rt=0]=sum=siz[v];
getrt(v,0);//Take the subtree with v as the root node as the object and find its center of gravity
getrt(rt,0);//Recalculate the siz with the center of gravity as the root node
divide(rt,0);
cout<<rt<<"rt\n";
}
return ;
}
void init(){
memset(vis,false,sizeof(vis));
memset(head,-1,sizeof(head));
return ;
}
int main(){
init();
scanf("%d",&n);
all = n*n;
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
build(u,v,w);
}
maxp[rt=0]=sum=n;
getrt(1,0);
getrt(rt,0);
divide(rt,0);
ans*=2;//Don't forget ans*2, because (3,5) and (5,3) are two answers
ans+=n;
int gcd = __gcd(ans,all);
ans/=gcd;
all/=gcd;
printf("%d/%d",ans,all);
return 0;
}
3.P4149 [IOI2011]Race
3.P4149 [IOI2011]Race
Analysis: this problem is a problem of 2011IOI, but it is not difficult. It just needs a little ingenious thought. This problem is to calculate the edge weight sum of a simple path as K, with the minimum number of edges and output the number of secondary edges. Obviously, the first step is to convert the edge weight into point weight (routine operation), and then the same processing method of point divide and conquer, Then use the point divide and conquer to treat each node as the root once. For each subtree with this node as the root node, calculate the distance from all nodes to the root node, and record it with the array. However, the maximum n here is 2e5 and the maximum edge weight is 1e6. Therefore, all edge weights of a path may exceed int and cannot be saved with the array, Therefore, we adopt the idea of pruning a little. We can see that the maximum K is only 1e6, so if the sum of edge weights of a path > k does not contribute to the answer, we will directly discard it, so we don't need to save it. Then we only need to open the size of the storage distance array to 1e6, so we can AC
AC Code:
#include<bits/stdc++.h>
using namespace std;
const int Maxn = 2e5+10;
const int N = 1e7+10;
int judge[N];
int n,k;
struct e{
int v;
int next;
int w;
}edge[Maxn*2];
int head[Maxn];
int cnt;
int siz[Maxn];
int maxp[Maxn];
int tmp[Maxn];
int dis[Maxn];
int ans;
int depp[Maxn];
bool vis[Maxn];
int sum,rt,tot;
void build(int u,int v,int w){
edge[++cnt].v = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
edge[++cnt].v = u;
edge[cnt].next = head[v];
head[v] = cnt;
edge[cnt].w = w;
return ;
}
/*Find the center of gravity and calculate the siz*/
void getrt(int u,int f){
siz[u] = 1;
maxp[u] = 0;
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].v;
if(v==f||vis[v]) continue;
getrt(v,u);
siz[u]+=siz[v];
if(siz[v]>maxp[u]) maxp[u] = siz[v];
}
maxp[u] = max(maxp[u],sum-maxp[u]);
if(maxp[u]<maxp[rt]) rt=u;
return ;
}
/*Processing distance*/
void getdis(int u,int f,int dep){
tmp[++tot] = dis[u];
//cout<<u<<' '<<dis[u]<<"gd\n";
depp[tot] = dep;
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
dis[v] = dis[u]+edge[i].w;
getdis(v,u,dep+1);
}
return ;
}
/*solve Processing node*/
void solve(int u){
static queue<int>q;
// cout<<u<<"u\n";
for(int i=head[u];i!=-1;i=edge[i].next){
tot = 0;
int v = edge[i].v;
if(vis[v]) continue;
dis[v]=edge[i].w;
getdis(v,u,1);
for(int i=1;i<=tot;i++){
if(k>=tmp[i])
q.push(tmp[i]);
if(k>=tmp[i])
ans = min(ans,depp[i]+judge[k-tmp[i]]);
}
/*Update path*/
for(int i=1;i<=tot;i++){
if(tmp[i]>k) continue;
judge[tmp[i]] = min(judge[tmp[i]],depp[i]);
}
}
while(!q.empty()){
judge[q.front()] = 0x3f3f3f3f;
q.pop();
}
return ;
}
/*Point divide and conquer*/
void divide(int u,int f){
vis[u] = true;
solve(u);
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(vis[v]||v==f) continue;
maxp[rt=0] = sum = siz[v];
getrt(v,0);
getrt(rt,0);
divide(rt,0);
// cout<<rt<<"rt\n";
}
return ;
}
void init(){
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
memset(judge,0x3f3f3f3f,sizeof(judge));
ans = 0x3f3f3f3f;
judge[0] = 0;
return ;
}
int main(){
init();
scanf("%d %d",&n,&k);
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
u++;v++;
build(u,v,w);
}
maxp[rt=0] = sum = n;
getrt(1,0);
getrt(rt,0);
//cout<<rt<<'\n';
divide(rt,0);
if(ans==0x3f3f3f3f) ans=-1;
cout<<ans<<'\n';
return 0;
}
4.CF161D Distance in Tree
4.CF161D Distance in Tree
Analysis: the idea of point divide and conquer is adopted, and the template can be set. There is no difficulty in thinking. The edge weight is not given to this question, and the default edge weight is 1. There is no need to look at longlong when it comes to Luogu, because the amount of data is small, but if it is on CodeForces, longlong needs to be opened
AC Code:
/*Point divide and conquer*/
#include<bits/stdc++.h>
#define ls dep<<1
#define rs dep<<1|1
using namespace std;
const int Maxn = 5e4+10;
struct e{
int w;
int v;
int next;
}edge[Maxn<<1];
int head[Maxn];
int n,k;
int cnt=0;
int siz[Maxn];
bool vis[Maxn];
int judge[Maxn];
int tmp[Maxn];
int tot=0;
int ans = 0;
int sum=0;
int rt;
int dis[Maxn];
int maxp[Maxn];
void build(int u,int v,int w){
edge[++cnt].v = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
edge[++cnt].v = u;
edge[cnt].next = head[v];
edge[cnt].w = w;
head[v] = cnt;
return ;
}
void getrt(int u,int f){
siz[u] = 1;
maxp[u] = 0;
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
getrt(v,u);
siz[u]+=siz[v];
if(siz[v]>maxp[u]) maxp[u] = siz[v];
}
maxp[u] = max(maxp[u],sum-maxp[u]);
if(maxp[u]<=maxp[rt]) rt = u;
return ;
}
void getdis(int u,int f){
tmp[++tot] = dis[u];
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
dis[v] = dis[u]+edge[i].w;
getdis(v,u);
}
return ;
}
void solve(int u){
static queue<int>q;
for(int i=head[u];i!=-1;i=edge[i].next){
tot = 0;
int v = edge[i].v;
if(vis[v]) continue;
dis[v] = edge[i].w;
getdis(v,u);
for(int i=1;i<=tot;i++){
if(tmp[i]==k) ans++;
else if(tmp[i]<k){
ans+=judge[k-tmp[i]];
}
}
for(int i=1;i<=tot;i++){
if(tmp[i]<k){
q.push(tmp[i]);
judge[tmp[i]]++;
}
}
}
while(!q.empty()){
judge[q.front()]--;
q.pop();
}
return ;
}
void divide(int u,int f){
vis[u] = true;
solve(u);
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
maxp[rt=0] = sum = siz[v];
getrt(v,0);
getrt(rt,0);
divide(rt,0);
}
return ;
}
void init(){
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
return ;
}
int main(){
init();
scanf("%d %d",&n,&k);
for(int i=1;i<n;i++){
int v,u;
scanf("%d %d",&v,&u);
build(v,u,1);
}
maxp[rt=0] = sum =n;
getrt(1,0);
getrt(rt,0);
divide(rt,0);
cout<<ans<<'\n';
return 0;
}
5.P4178 Tree
P4178 Tree
Analysis: this question is similar to question 4. This question is to calculate the logarithm of points whose distance between two points is less than or equal to K, so we still use the idea of point divide and conquer to deal with each point, but we need to use the segment tree to maintain the number of points whose distance to the root node is i, Then, use the interval query to quickly query the number of root nodes with a distance of [1,i] (note that this problem is still true. If the path length is greater than k, cut it directly, otherwise the array cannot be saved)
AC Code:
#include<bits/stdc++.h>
#define ls dep<<1
#define rs dep<<1|1
using namespace std;
const int Maxn = 4e4+10;
struct e{
int w;
int v;
int next;
}edge[Maxn<<1];
int tr[Maxn*4]={0};//Segment tree maintenance interval and
int cnt;
bool vis[Maxn];
int head[Maxn];
int maxp[Maxn];
int dis[Maxn];
int ans;
int siz[Maxn];
int judge[Maxn];
int num=0;
int tmp[Maxn];
int rt,sum,tot;
int n,k;
void pushup(int dep){
tr[dep] = tr[ls]+tr[rs];
return ;
}
void update(int l,int r,int ql,int qr,int dep,int val){
if(ql<=l&&r<=qr){
tr[dep] += (r-l+1)*val;
return ;
}
int mid = l+r>>1;
if(ql<=mid) update(l,mid,ql,qr,ls,val);
if(qr>mid) update(mid+1,r,ql,qr,rs,val);
pushup(dep);
return ;
}
int query(int l,int r,int ql,int qr,int dep){
if(ql<=l&&r<=qr){
return tr[dep];
}
int mid = l+r>>1;
int ans = 0;
if(ql<=mid) ans+=query(l,mid,ql,qr,ls);
if(qr>mid) ans+=query(mid+1,r,ql,qr,rs);
return ans;
}
void build(int u,int v,int w){
edge[++cnt].v = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
edge[++cnt].v = u;
edge[cnt].next = head[v];
edge[cnt].w = w;
head[v] = cnt;
return ;
}
/*Find the center of gravity and calculate the siz*/
void getrt(int u,int f){
maxp[u] = 0;
siz[u] = 1;
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].v;
if(v==f||vis[v]) continue;
getrt(v,u);
siz[u]+=siz[v];
if(siz[v]>maxp[u]) maxp[u] = siz[v];
}
maxp[u] = max(maxp[u],sum-maxp[u]);
if(maxp[u]<=maxp[rt]) rt=u;
return ;
}
/*Processing dis*/
void getdis(int u,int f){
tmp[++tot] = dis[u];
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].v;
if(v==f||vis[v]) continue;
dis[v] = dis[u]+edge[i].w;
getdis(v,u);
}
return ;
}
/*solve Processing node*/
void solve(int u){
for(int i=head[u];i!=-1;i=edge[i].next){
tot = 0;
int v = edge[i].v;
if(vis[v]) continue;
dis[v] = edge[i].w;
getdis(v,u);
for(int i=1;i<=tot;i++){
if(tmp[i]==k){
ans++;
}
else if(tmp[i]<k){
ans++;
/*Calculate the number of points whose distance to u node is [1,k-tmp[i]]*/
ans+=query(1,k,1,k-tmp[i],1);
}
}
for(int i=1;i<=tot;i++){
/*>k Don't contribute to the answer*/
if(tmp[i]<=k){
judge[++num] = tmp[i];
update(1,k,tmp[i],tmp[i],1,1);
}
}
}
for(int i=1;i<=num;i++){
update(1,k,judge[i],judge[i],1,-1);
}
return ;
}
/*Point divide and conquer*/
void divide(int u,int f){
vis[u] = true;
solve(u);
for(int i=head[u];i!=-1;i=edge[i].next){
num = 0;
int v = edge[i].v;
if(v==f||vis[v]) continue;
maxp[rt=0] = sum = siz[v];
getrt(v,0);
getrt(rt,0);
divide(rt,0);
}
return ;
}
void init()
{
memset(head,-1,sizeof(head));
memset(vis,false,sizeof(vis));
//memset(judge,0,sizeof(vis))
return ;
}
int main(){
init();
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
build(v,u,w);
}
scanf("%d",&k);
maxp[rt=0]=sum=n;
getrt(1,0);
getrt(rt,0);
divide(rt,0);
cout<<ans<<'\n';
}