--From Nanchang Institute of Technology ACM intense training team

This week, I learned how to solve the problem of line segment tree and scan line. Here is a brief introduction by the chicken:
Generally, the simplest problem of scan line is the bare template of scan line (generally speaking, the data range is small). Secondly, it is expanded into segment tree + scan line (the data range is increased). The more difficult thing is scan line + segment tree + Plus discretization.

Scan line

What is a scan line
Give you a bunch of rectangles and find the area when these rectangles overlap again? You need a scan line

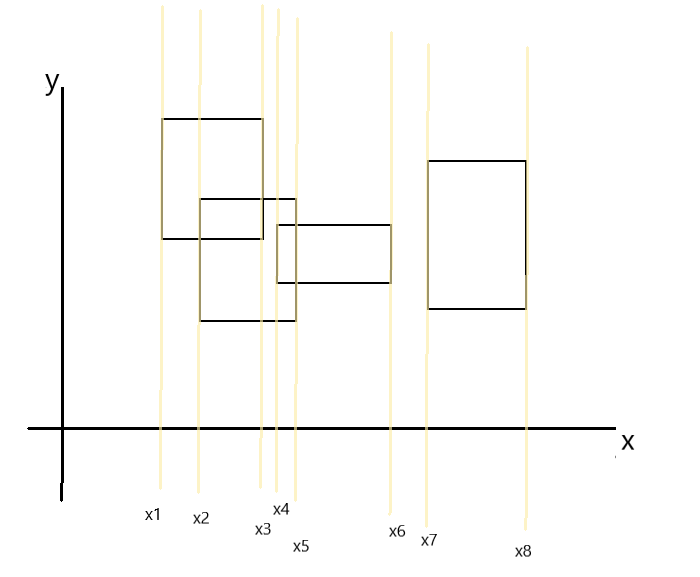
Sort from small to large xi(1~8) according to X. after this processing, we can see that the values of each two adjacent xi divide the rectangle into several rectangles. Here, we record the upper length Y2 and the lower length Y1. The answer to the total area ans + = (x2-x1) * (y2-y1) is added before every two xi and belongs to the topic rectangle, which also involves an interval merging (for example, the matrix formed by X2 to x3).

Scanline + line segment tree
Example: paint area
A group of archaeological robots on Planet X are archaeological on a piece of ruins.
The ground in this area is as hard as stone and as flat as a mirror.
For the convenience of managers, a standard rectangular coordinate system is established.
Each robot has its own specialty and unique skills.
They are also interested in different contents.
After various measurements, each robot will report one or more rectangular areas as priority archaeological areas.
The representation format of the rectangle is (x1,y1,x2,y2), representing the coordinates of the two diagonal points of the rectangle.
In order to be eye-catching, the headquarters requires that the rectangular areas selected by all robots be painted with yellow paint.
Xiao Ming doesn't need to be a painter, but he needs to calculate how much paint it will cost.
In fact, it's not difficult. Just calculate the total area covered by all rectangles.
Note that the rectangles may overlap.

Input format
The first line, an integer n, indicates how many rectangles there are.
In the next n lines, each line has four integers x1,y1,x2,y2, separated by spaces, representing the coordinates of the two diagonal vertices of the rectangle.
Output format
One integer per line represents the total area covered by the rectangle.
Data range
1≤n≤10000,
0≤x1,x2,y2,y2≤10000
Data guarantee X1 < x2 and Y1 < Y2.
Input sample:
3
5 2 10 6
2 7 12 10
8 1 15 15
output
128

The structure needs to save the quad (x, y1, y2, k). X represents the position of this edge on the x-axis, and y1 and y2 represent the lower and upper limits of this edge on X. k indicates the mark.

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=10100;//Data range
 int ls(int x){//Left node
 	return x<<1;
 } 
 int rs(int x){//Right node
 	return x<<1|1;
 }
 struct node{
 	int x,y1,y2;//X represents the position of this edge in the x-axis, y1 and y2 represent the lower and upper limits of this edge in X
 	int k;//k indicates the mark.
 }seg[N*2];//A matrix has two sides parallel to the y axis, so multiply by 2
 struct Node{
 	int l,r;
 	int cnt,len;
 }; 
 Node tree[N*4];//Storage size of the built tree
 int n;
 void build(int l,int r,int u){//Build segment tree
 	tree[u]={l,r};
	 if(r==l)
 		return ;
 	int mid=(l+r)>>1;
 	build(l,mid,ls(u));
 	build(mid+1,r,rs(u));
 }
 void push_up(int p){//Update up
 	if(tree[p].cnt>0){
 		tree[p].len=tree[p].r-tree[p].l+1;
	 }
	 else if(tree[p].l==tree[p].r) tree[p].len=0;
	 else tree[p].len=(tree[ls(p)].len+tree[rs(p)].len);
 }
bool cmp(node a,node b){
	return a.x<b.x;
} 
void modify(int u,int l,int r,int k){//Updates each edge parallel to the Y axis
	if(tree[u].l>=l&&tree[u].r<=r){
		tree[u].cnt+=k;
		push_up(u);
	}else{
	int mid=(tree[u].r+tree[u].l)>>1;
	if(mid>=l){
		modify(ls(u),l,r,k);
	}
	if(mid<r){
		modify(rs(u),l,r,k);
	}
	push_up(u);
	}
}
 int main(){
 	cin>>n;
 	int m=0;
 	for(int i=1;i<=n;i++){
 		int x1,x2,y1,y2;
		cin>>x1>>y1>>x2>>y2;
 		seg[m++]={x1,y1,y2,1};//Save positive mark every time
 		seg[m++]={x2,y1,y2,-1};
	 }
	 sort(seg,seg+m,cmp); //After sorting from small to large according to the size of x, it is still marked first (referring to two edges of the same matrix)
	 build(0,10000,1);
	 int ans=0;
	 for(int i = 0; i < m; i ++){
	 	if(i>0) ans+=tree[1].len*(seg[i].x-seg[i-1].x);//Each addition is the part between two adjacent xi and in the rectangle.
	 	modify(1,seg[i].y1,seg[i].y2-1,seg[i].k);
	 }
	 cout<<ans<<endl;
	 return 0;
 } 

Discretization:

vector<int> mp;
for(int i=0;i<=n;i++)
mp.push_back(a[i]);
sort(mp.begin().mp.end());
mp.erase(unique(mp.begin(),mp.end()),mp.end());

Segment tree + scanline + discretization

Discretization: discretization of coordinates
Dichotomy: discretization dichotomy
Scanline: large data range, two-dimensional, or scanline
Segment tree: large data range, interval additivity, a pile of interval operations, or segment tree

Example: stars in AcWing248 window
There are many stars in a sky (regarded as a plane rectangular coordinate system), and the coordinates and brightness of each star are known (all integers).
Find the maximum total brightness of the stars that can be surrounded by a rectangular window with width W and height H (W,H is a positive integer). (stars on the rectangular boundary do not count)

Input format
The input contains multiple sets of test cases.
The first line of each use case contains three integers: n, W, H, indicating the number of stars and the width and height of the rectangular window. Then there are n lines, each line has three integers: X, y, c, representing the position (x, y) and brightness of each star. No two stars are at the same point.

Output format
Each test case outputs a maximum sum of brightness.

One line for each result.

Data range
1≤n≤10000,
1≤W,H≤1000000,
0≤x,y<231
Input sample:
3 5 4
1 2 3
2 3 2
6 3 1
3 5 4
1 2 3
2 3 2
5 3 1
The problem is transformed into: there are several regions on the plane, each region has a weight, and the weight sum of the overlapping regions on which coordinate is the largest is calculated Remember, each area is produced by a star, and the weight is equal to the brightness of the star It should be noted here that the stars on the boundary of the matrix with length W and height H are not counted, so pay attention when building trees later.

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=10100;
 vector<ll> mp;
 int ls(int x){
 	return x<<1;
 } 
 int rs(int x){
 	return x<<1|1;
 }
 struct node{
 	ll x,y1,y2;
 	ll k;
 }seg[N*2];
 struct Node{
 	ll l,r;
 	ll cnt,len;
 }; 
 Node tree[N*8];
 ll n;
 void build(ll l,ll r,ll u){
 	tree[u]={mp[l],mp[r],0,0};
	 if(r - l == 1)//Consider that adjacent cannot be.
 		return ;
 	ll mid=(l+r)>>1;
 	build(l,mid,ls(u));
 	build(mid,r,rs(u));
 }
void  push_up(ll p){
 	tree[p].len=max(tree[rs(p)].len,tree[ls(p)].len)+tree[p].cnt;
 }
bool cmp(node a,node b){
	return a.x<b.x|| (a.x==b.x && a.k<0);
} 
void modify(ll u,ll l,ll r,ll k){
	if(tree[u].l>=l&&tree[u].r<=r){
		tree[u].cnt+=k;
		tree[u].len+=k; 
		return ;
		}
		ll mid=l+r>>1;
	if(l<tree[ls(u)].r){
		modify(ls(u),l,min(r,tree[ls(u)].r),k);
	}
	if(r>tree[rs(u)].l){
		modify(rs(u),max(l,tree[rs(u)].l),r,k);
	}
	push_up(u);
}
 int main(){
 	ll n,h,w;
 	while(cin>>n>>w>>h){
 		ll m=0;
 	for(int i=1;i<=n;i++){
 		ll x,y,k;
		cin>>x>>y>>k;
 		seg[m++]={x,y,y+h,k};
 		seg[m++]={x+w,y,y+h,-k};
 		mp.push_back(y);
 		mp.push_back(y+h);
	 }
	 sort(seg,seg+m,cmp); 
	 sort(mp.begin(),mp.end());
	 mp.erase(unique(mp.begin(),mp.end()),mp.end());
	 build(0,mp.size()-1,1);
	 ll ans=0;
	 for(int i = 0; i < m; i ++){
	 	int tmp=lower_bound(mp.begin(),mp.end(),seg[i].y1)-mp.begin();
	 	int tmp1=lower_bound(mp.begin(),mp.end(),seg[i].y2)-mp.begin();
	 	modify(1,mp[tmp],mp[tmp1],seg[i].k);
	 	if(seg[i].k>0)ans=max(ans,tree[1].len);
	 }
	 cout<<ans<<endl;
	 }
 	
	 return 0;
 } ```