Title Description

This is the * * JZ 58 symmetric binary tree on Niuke. The difficulty is * *.

Tag: "sword finger Offer", "binary tree", "sequence traversal", "iteration", "recursion"

Description:

Please implement a function to judge whether a binary tree is symmetrical.

Note that if a binary tree is the same as the mirror image of the binary tree, it is defined as symmetric.

Example 1

Input:{8,6,6,5,7,7,5}

Return value: true

Example 2

Input:{8,6,9,5,7,7,5}

Return value: false

requirement:

• Time: 1 s

• Space: 64 M

basic thought

First of all, it should be clear that the "symmetry" defined by the topic is to consider empty nodes for each layer at the same time.

Therefore, if we use the conventional traversal method to check, we need to represent the empty node.

Local inspection (sequence traversal)

We use 0x3f3f3f3f3f as an invalid value and create a placeholder node emptyNode to refer to an empty node (emptyNode.val = 0x3f3f3f3f).

A simple approach is to use "sequence traversal" to "check layer by layer", and use emptyNode to refer to empty nodes, while ensuring that the child nodes corresponding to emptyNode are not recursive.

The specific methods are as follows:

1. At the beginning, join the root node into the queue;

2. Take out the node from the queue and check whether the node is an emptyNode node to decide whether to continue to join the queue:

• When it is not an emptyNode node, join its left / right son. If there is no left / right son, join the team with emptyNode instead;

• When it is an emptyNode node, it is ignored;

1. During the process, use the "temporary list" to record the information of the current layer, and check whether the current layer meets the "symmetry" requirements;

2. Cycle through the process and until the entire queue is empty.

code:

import java.util.*;
class Solution {
    int INF = 0x3f3f3f3f;
    TreeNode emptyNode = new TreeNode(INF);
    boolean isSymmetrical(TreeNode root) {
        if (root == null) return true;

        Deque<TreeNode> d = new ArrayDeque<>();
        d.add(root);
        while (!d.isEmpty()) {
            //Each cycle expands the next layer and coexists in the "queue"
            //At the same time, the node values of this layer are successively stored in the "temporary list"
            int size  = d.size();
            List<Integer> list = new ArrayList<>();
            while (size-- > 0) {
                TreeNode poll = d.pollFirst();
                if (!poll.equals(emptyNode)) {
                    d.addLast(poll.left != null ? poll.left : emptyNode);
                    d.addLast(poll.right != null ? poll.right : emptyNode);
                }
                list.add(poll.val);
            }
            
            //After each layer is expanded, check whether the layer storing the current layer meets the "symmetry" requirements
            if (!check(list)) return false;
        }
        return true;
    }

    //Use the "double pointer" to check whether a layer meets the "symmetry" requirement
    boolean check(List<Integer> list) {
        int l = 0, r = list.size() - 1;
        while (l < r) {
            if (!list.get(l).equals(list.get(r))) return false;
            l++;
            r--;
        }
        return true;
    }
}

• Time complexity: in the process of sequence traversal, each node can join the queue at most once, and each layer will only be checked once in the process of checking symmetry. Complexity is

• Space complexity:

Global check (recursive)

In the "sequence traversal" solution, we use the "symmetry" definition to check each layer.

In essence, this is a multiple "local" check using the "symmetry" definition.

In fact, we can also use the definition of "symmetry" to check at the "overall" level.

How do we define whether two subtrees a and b are "symmetric"?

The "symmetry" requirement is met if and only if two subtrees meet the following requirements:

1. The root node values of the two sub trees are the same;

2. The left and right subtrees of the two subtrees are symmetrical respectively, including:

• The values of the corresponding positions of the left subtree of a tree and the right subtree of b tree are equal

• The values of the corresponding positions of the right subtree of a tree and the left subtree of b tree are equal

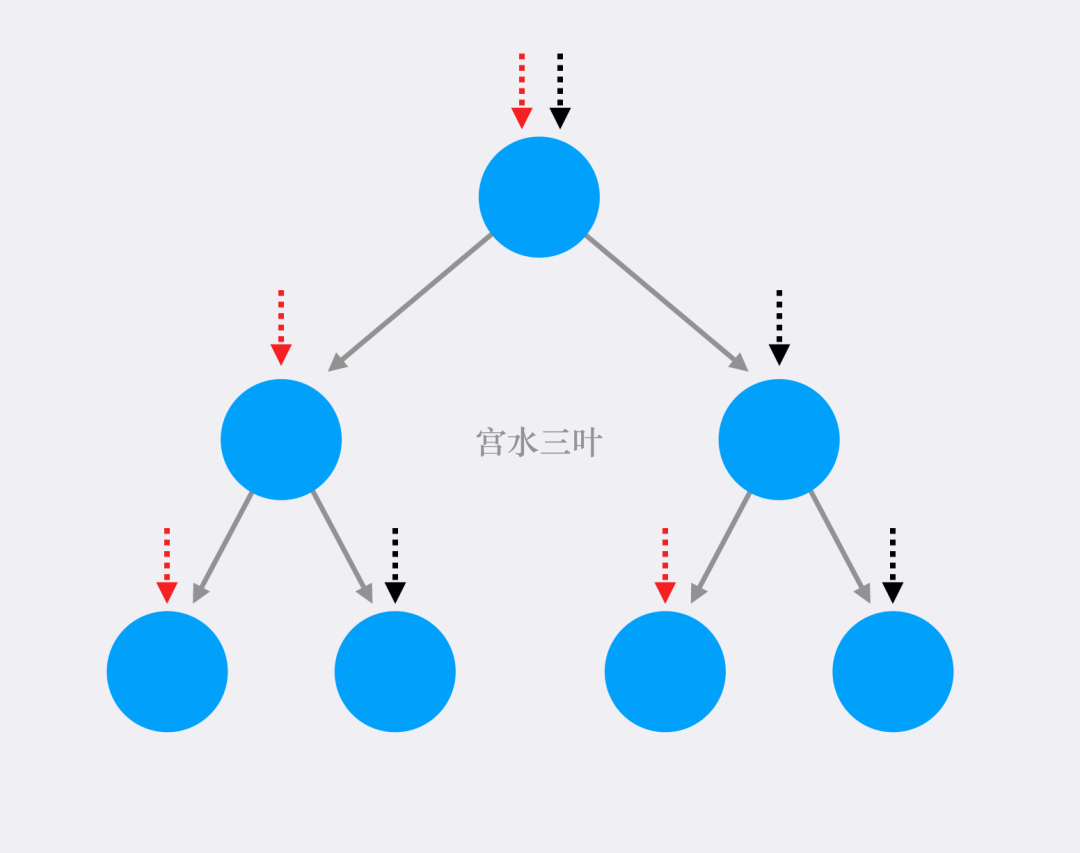
Specifically, we can design a recursive function check to pass in the head nodes a and b of the two subtrees to be tested (for this problem, we can pass in root). In a single query, there is the following obvious Base Case to judge whether the subtree is "symmetrical":

• Both a and b are empty nodes: meet the requirements of "symmetry";

• One of the nodes a and b is empty, which does not meet the "symmetry" requirement;

• The values of a and b are not equal and do not meet the requirements of "symmetry";

In other cases, we should check whether the left and right nodes of a and B are "symmetrical", that is, recursively call check(a.left, b.right) and check(a.right, b.left).

code:

class Solution {
    public boolean isSymmetrical(TreeNode root) {
        return check(root, root);
    }
    boolean check(TreeNode a, TreeNode b) {
        if (a == null && b == null) return true;
        if (a == null || b == null) return false;
        if (a.val != b.val) return false;
        return check(a.left, b.right) && check(a.right, b.left);
    }
}

• Time complexity: each node is accessed only once. Complexity is

• Space complexity:

summary

The above two solutions are not only different in implementation, but also different in "starting point":

• Solution 1: use the method of "sequence traversal" to check the "symmetry" in the unit of "layer";

• Solution 2: use the method of "recursive tree expansion" to check the "symmetry" in the unit of "subtree".

When we consider from the overall level, with recursion, we can often write much simpler code than the conventional practice.

I suggest you deepen your understanding of the two different starting points of "part" and "whole".

last

This is the 58th article in our "selected sword fingers" series, which began on July 1, 2021.

This series will cover all the classic and timeless topics in "sword finger Offer".

While providing the pursuit of "proof" & "ideas", it also provides the most concise code.

Welcome to pay attention and make a friend ω ・´)