In my junior year, writing a blog is my experience of the recent course design for your reference.
design sketch:
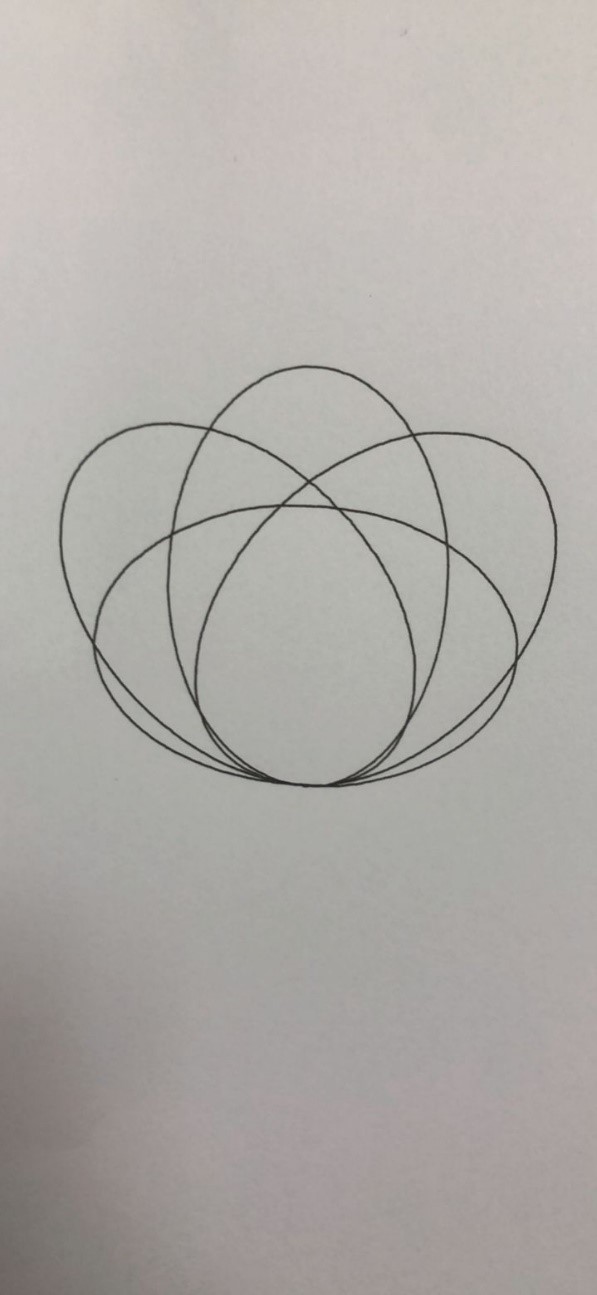
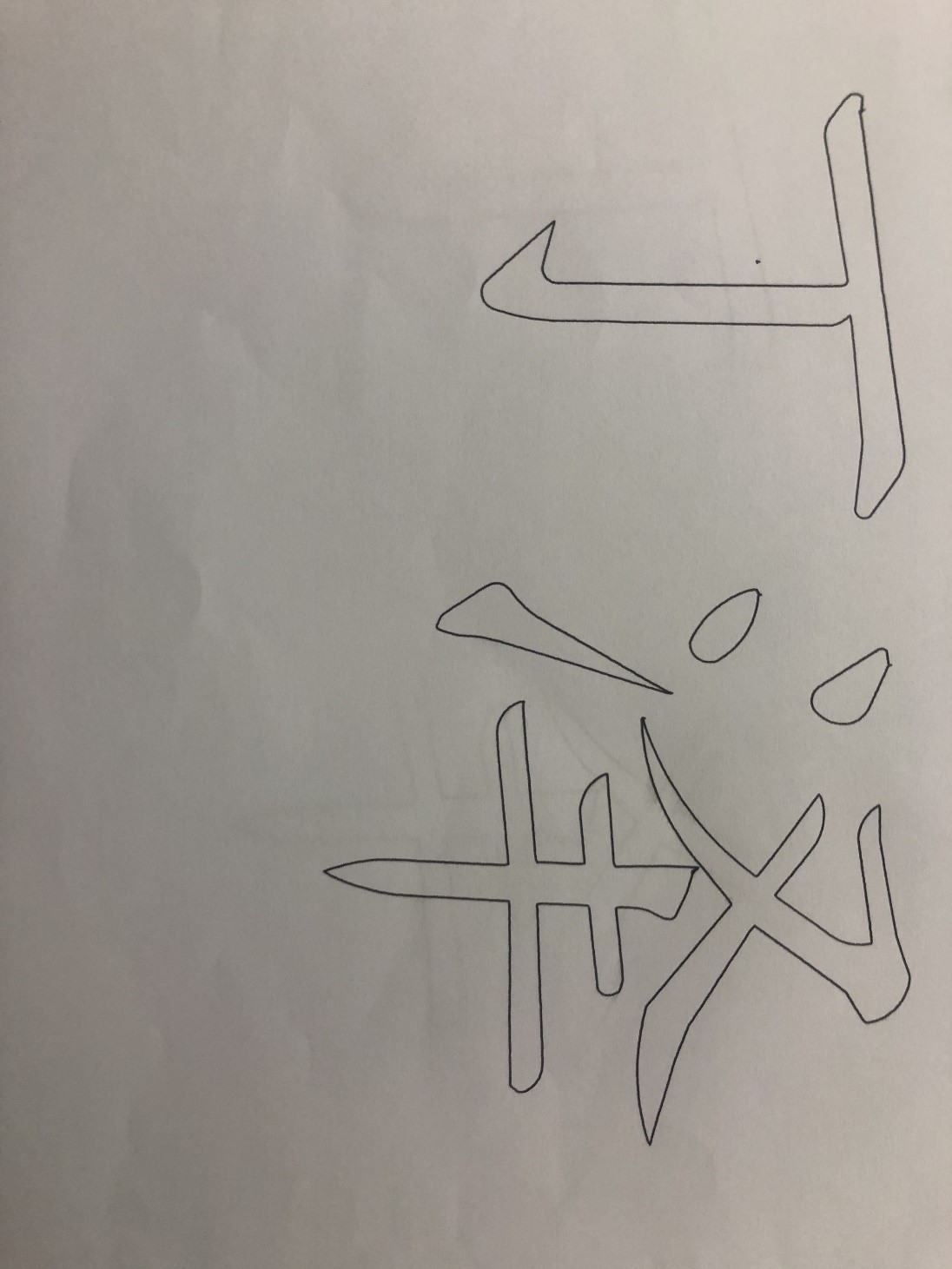
First introduce the experimental equipment used this time:
Cross slide, two stepping motors, a steering gear, an STM32 development board and a pen.
The required software is Keil5 and CAD. python and matlab are useful in the ellipse interpolation algorithm, only to verify the algorithm.
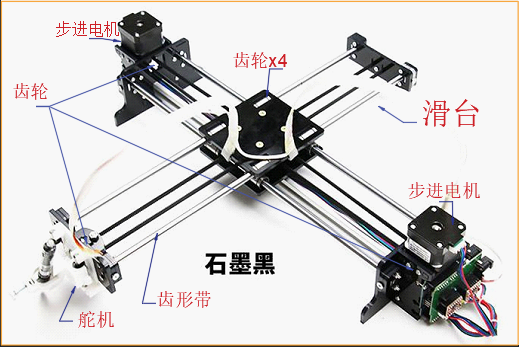
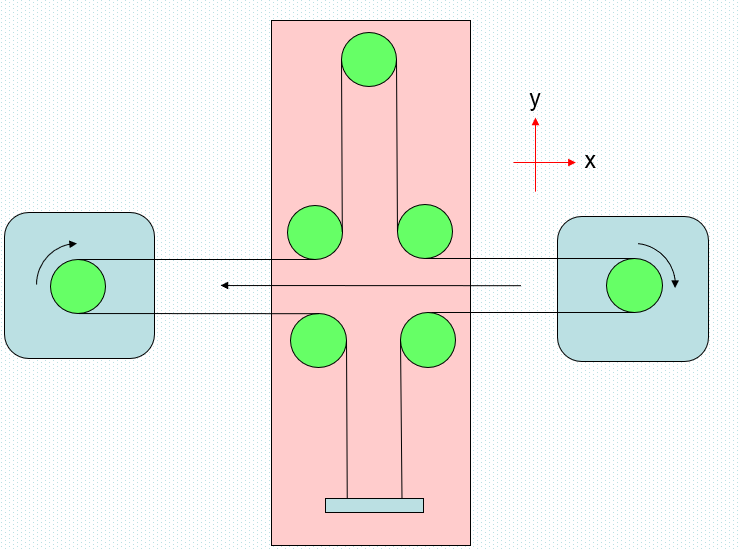
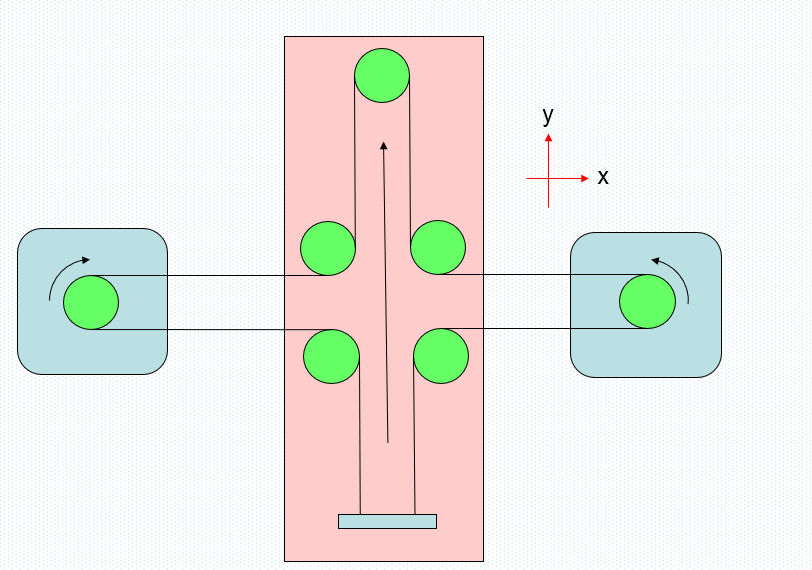
x. The movement in the Y direction is controlled by controlling the steering of the stepper motor.
I use the relative coordinate system. Personally, I think it has more advantages.
Specific experimental steps:
1. Measure the step distance of stepping motor.
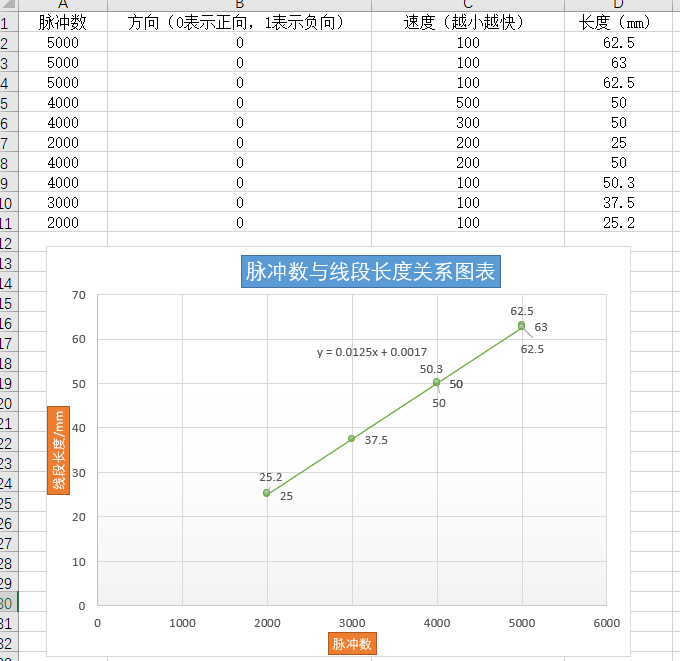
About 800 plus / cm, i.e. 80 plus / mm.
2. Steering gear lifting and lowering angle setting
Set it by yourself. In the code I give, the pen is 120 ° when lifted and 50 ° when lowered.
3. Write function of mobile pen
4. Write linear interpolation function
5. Write arc interpolation function
6. Key control entry is added to the main program. How to identify each function command?
7. Track command area (two-dimensional array is more appropriate) and defined as a global variable. (it will be too small to write in main)
The specific codes are as follows:
#include "stdio.h"
#include "stdlib.h" / / absolute value is used
#include "stm32f10x.h"
#include "hal.h"
#include "key.h"
#include "lcd_dis24.h"
#include "delay.h"
#include "motor.h"
#include "pwm.h"
#include "adc.h"
#include "user.h"
#define u16 unsigned int
#define u8 unsigned char
void TIM2_IRQHandler(void);
void MotorXDriver(u16 plus,u8 dir,u16 time);
void MotorYDriver(u16 plus,u8 dir,u16 time);
void Move(int x1,int y1);
void DrawLine(int x1,int y1);
void DrawCricle1(int x0,int y0,int x1,int y1,u16 r,u16 q);//Inverse circle
void DrawCricle2(int x0,int y0,int x1,int y1,u16 r,u16 q);//CIS circle
u8 key_num = 0;
u8 key_last = 0;
u8 time_500us_ok = 0;
u8 time_1s_ok = 0;
u8 time_10ms_ok = 0;
u8 servo = 0,dir = 0;
u16 i=0;
const int fangdayinzi = 8;// Magnification factor 80plus/mm
int point[150][7];
//Define the path coordinates to go 100um
//Subscript 0:1-straight line, 2-inverse circle, 0-mobile pen, 3-cis circle
//Subscript 1: x0, modified, default to 0
//Subscript 2: y0, modified, defaults to 0
//Subscript 3: x1 / / only end coordinates are required for linear interpolation
//Subscript 4: y1
//Subscript 5: r / / radius
//Subscript 6: q / / quadrant position
int point[150][7]={
//ze
{1,-22,-4},
{2,-9,7,-11,0,11,2},
{2,-11,0,-7,-8,11,3},
{1,54,-75},
{2,-24,-9,0,-25,25,3},
{2,0,-25,19,-16,25,4},
{2,33,-34,47,0,47,4},
{2,47,0,20,43,47,1},
{1,-63,25}, //The first point ends
{0,-97,-194},
{1,-10,-3},
{2,-136,-38,-50,-132,141,3},
{2,0,-28,28,0,28,4},
{2,28,0,20,20,28,1},
{2,97,69,0,119,119,1}, // Finish the second point
{0,153,-124},
{1,-106,-201},
{3,129,-82,88,-125,153,4},
{2,-18,21,-27,0,27,2},
{2,-27,0,-25,-11,27,3},
{1,52,-73},
{1,21,-7},
{1,9,32},
{3,-344,0,-336,73,344,2},
{1,65,250}, //Finish drawing
{0,39,-38},
{2,150,-429,378,-252,454,4},
{1,-131,87},
{3,-36,77,0,85,85,2},
{3,0,85,44,73,85,1},
{1,78,-56},
{1,53,83},
{2,61,-43,75,0,75,4},
{2,75,0,71,23,75,1},
{1,-156,-29},
{3,0,-61,-52,-32,61,3},
{1,55,3},
{1,146,33},
{1,54,21},
{3,0,75,74,13,75,1},
{1,-47,-31},
{1,-93,-141},
{1,159,-89},
{1,52,-17},
{1,133,-31},
{3,133,-355,0,-379,379,4},
{3,0,-379,-82,-370,379,3},
{1,-160,119},
{1,-56,-50},
{3,236,-249,22,-342,343,4}, //Finish writing again
{0,220,87},
{1,5,-120},
{1,-140,-15},
{2,-61,-27,0,-66,66,3},
{1,79,10},
{1,0,-73},
{1,-231,-28},
{1,-12,1},
{2,-54,-16,0,-56,56,3},
{1,197,26},
{1,0,-170},
{2,-277,0,-254,-111,277,3},
{2,290,-133,319,0,319,4},
{1,0,152},
{1,280,13},
{1,9,13},
{2,47,14,0,49,49,1},
{1,-242,-20},
{1,0,78},
{1,121,18},
{2,0,-13,13,0,13,4},
{2,31,0,22,21,31,1},
{1,-18,4},
{1,-108,-16},
{1,0,23},
{3,-89,0,-77,44,89,2},
{2,12,-10,15,0,15,4},
{2,15,0,8,13,15,1},
{1,-40,16},
{1,-28,7}, //80 lines in total
};
int main(void)
{
ChipHalInit(); //On chip hardware initialization
ChipOutHalInit(); //Off chip hardware initialization
//Tim8 channels 1 and 2 are
SetTim8Pwm(1,0);
SetTim8Pwm(2,0);
SetTim8Pwm(3,500); //TIM8
SetTim4Pwm(1,0);
SetTim4Pwm(2,0);
SetTim4Pwm(3,0);
SetTim4Pwm(4,0);
//duoji taiqi 50
//duoji fangxia 120
LCD_Display("ADC1: ADC2: ADC3: ADC4: ADC5: ADC6: ADC7: ADC8: ADC9: ADC10: ",0,16,0,0xffff);
LCD_Display("DIN1: DIN2: DIN3: DIN4: DIN5: DIN6: DIN7: DIN8: DIN9: DIN10: DIN11: DIN12: ",0,80,0,0xffff);
LCD_Display("Key: ",50,176,0,0xffff);
LCD_Display("electric machinery: ",50,160,0,0xffff);
LCD_Display("shut",100,160,0xf800,0xffff);
// LCD_Display("123",100,160,0xf800,0xffff);
while (1)
{
time_10ms_ok = 1;
if(time_10ms_ok == 1)//Functions executed once in 10ms, such as keyboard scanning
{
time_10ms_ok = 0;
key_num = key();
if(key_num != key_last)
{
key_last = key_num;
if((key_num >= '0' && key_num <= '9') || key_num == '*' || key_num == '#') //Press 0-9 or *#
{
LCD_write_EN(key_num,100,176,0xf800,0xffff);//Directly display 0-9 or * # key value
}
if(key_num == '4')
{
MotorXDriver(4000,1,100);
}
else if(key_num == '2')
{
MotorYDriver(2000,0,100);
}
else if(key_num =='6')
{
MotorXDriver(4000,0,100);
}
else if(key_num == '8')
{
MotorYDriver(1500,1,100);
}
else if(key_num == '1')
{
SetTim4Pwm(1,50);
}
else if(key_num == '3')
{
SetTim4Pwm(1,120);
}
else if(key_num == '0')
{
SetOutPut(11,1);
SetTim8Pwm(1,120);//Lift the pen
key_num = key();//Read key
if(key_num == '0')//Press the number 0
{
//mapping
for(i=0;i<80;i++)
{
//Start drawing
if(point[i][0]==1)//1 represents a straight line
{
DrawLine((fangdayinzi*point[i][3]),(fangdayinzi*point[i][4]));
}
else if(point[i][0]==2)//2 represents arc (inverse circle)
{
DrawCricle1((fangdayinzi*point[i][1]),(fangdayinzi*point[i][2]),(fangdayinzi*point[i][3]), (fangdayinzi*point[i][4]), (fangdayinzi*point[i][5]), point[i][6]);
}
else if(point[i][0]==3)//3 represents arc (along circle)
{ DrawCricle2((fangdayinzi*point[i][1]),(fangdayinzi*point[i][2]),(fangdayinzi*point[i][3]), (fangdayinzi*point[i][4]), (fangdayinzi*point[i][5]), point[i][6]);
}
else if(point[i][0]==0)//0 - Mobile pen
{ Move((fangdayinzi*point[i][3]),(fangdayinzi*point[i][4]));
}
}
SetTim4Pwm(1,120);
break;
}
}
else if(key_num == '*')
{
SetOutPut(10,1);
}
else if(key_num == '#')
{
SetOutPut(12,1);
}
servo = 0;
LCD_Display("shut",100,160,0xf800,0xffff);
}
else if(key_num >= 'A' && key_num <= 'D')//Press F1-F4
{
//The key value is' A '-'D' is the key value of F1-F4, which is displayed after conversion
switch(key_num)
{
case 'A':LCD_Display("F1",100,176,0xf800,0xffff);\
SetTim4Pwm(1,45);SetTim4Pwm(2,90);\
SetTim4Pwm(3,135);SetTim4Pwm(4,180);\
LCD_Display("openª",100,160,0xf800,0xffff);\
servo = 1;break;
case 'B':LCD_Display("F2",100,176,0xf800,0xffff);break;
case 'C':LCD_Display("F3",100,176,0xf800,0xffff);break;
case 'D':LCD_Display("F4",100,176,0xf800,0xffff);break;
}
}
else
{
LCD_Display(" ",100,176,0,0xffff);//Clear the key value display after releasing the key
if(servo == 0)
SetOutPut(0,0);
}
}
}
return 0;
}
//TIM2 interrupt function, 500us interrupt once, this function cannot be deleted, otherwise burning will fail
void TIM2_IRQHandler(void)
{
u8 time_counter_1s = 0;
u8 time_counter_10ms = 0;
if (TIM_GetITStatus(TIM2, TIM_IT_Update) == SET)
{
time_500us_ok = 1;
if(++ time_counter_10ms >= 20)
{
time_counter_10ms = 0;
time_10ms_ok = 1;
if(++ time_counter_1s >= 50)
{
time_counter_1s = 0;
time_1s_ok = 1;
}
}
}
if(TIM_GetITStatus(TIM2, TIM_IT_Update) != RESET)
{
TIM_ClearITPendingBit(TIM2, TIM_IT_Update);
}
}
//X motor drive function, two motors rotate in the same direction
void MotorXDriver(u16 plus,u8 dir,u16 time)
{
u16 i;
//Direction control
if(dir == 1) //Left, 1 left
{
DIR1_L();
DIR2_L();
}
else
{
DIR1_H();
DIR2_H();
}
//Pulse control
for(i =0;i<plus;i++)
{
PUL1_H();
PUL2_H();
delay_us(time);
PUL1_L();
PUL2_L();
delay_us(time);
}
}
//Y motor drive function, two motors rotate in reverse
void MotorYDriver(u16 plus,u8 dir,u16 time)
{
u16 i;
//Direction control
if(dir == 1) //Down, 1 means down
{
DIR1_L();
DIR2_H();
}
else
{
DIR1_H();
DIR2_L();
}
//Pulse control
for(i =0;i<plus;i++)
{
PUL1_H();
PUL2_H();
delay_us(time);
PUL1_L();
PUL2_L();
delay_us(time);
}
}
//Move pen function
void Move(int x1,int y1)
{
//Lift the pen
SetTim4Pwm(1,120);
delay_ms(500);
//Move in x direction
if(x1>=0)
MotorXDriver(x1,0,500); //Move x1
else
MotorXDriver(-x1,1,500);
//Move in y direction
if(y1>=0)
MotorYDriver(y1,0,500);
else
MotorYDriver(-y1,1,500);
SetTim4Pwm(1,50);
delay_s(1);//Make sure you really put it down
}
//Draw a straight line function (you can draw a horizontal line and a plumb line)
void DrawLine(int x1,int y1) //Give end coordinates
{
//Define local variables
long Fm = 0; //Define the deviation judgment of each step
int x0 = 0, y0= 0; //x0 and y0 are the current coordinates and initialized to 0
u16 number_xy; //Define steps
//Linear interpolation
if(x1>0&&y1>=0) //The end coordinate is in the first quadrant (including x positive half axis and excluding y positive half axis)
{
number_xy = (x1+y1);
while(1)
{ //turn right
if(Fm>=0 && number_xy>0) //FM > = 0 and not finished. Take the number of steps as the jump condition, which is the finishing touch
{
Fm -= y1;
x0 += 1;
y0 = y0;
MotorXDriver(1,0,500); //Call the motor driver, turn forward, step by step, so my accuracy is quite high
number_xy --;
}
// Go up
if(Fm<0 && number_xy>0) //FM < 0 and not finished
{
Fm += x1;
x0 = x0;
y0 += 1;
MotorYDriver(1,0,500); //Call motor driver, forward rotation
number_xy --;
}
if(number_xy <= 0) //Jump out after writing
break;
if(x0 == x1 && y0 == y1)//Write and jump out
break;
}
}
if(x1<=0&&y1>0) //The end coordinate is in the second quadrant (including y positive half axis and excluding x negative half axis)
{
x1 = abs(x1);
number_xy = (x1+y1);
while(1)
{ //turn left
if(Fm>=0 && number_xy>0) //FM > = 0 and not finished
{
Fm -= y1;
x0 += 1;
y0 = y0;
MotorXDriver(1,1,500); //Call the motor driver and reverse
number_xy --;
}
// Go up
if(Fm<0 && number_xy>0) //FM < 0 and not finished
{
Fm += x1;
x0 = x0;
y0 += 1;
MotorYDriver(1,0,500); //Call motor driver, forward rotation
number_xy --;
}
if(number_xy <=0) //Jump out after writing
break;
if(x0 == x1 && y0 == y1)
break;
}
}
if(x1<0&&y1<=0) //The end coordinate is in the third quadrant (including x negative half axis and excluding y negative half axis)
{
x1 = abs(x1);
y1 = abs(y1);
number_xy = (x1+y1);
while(1)
{ //turn left
if(Fm>=0 && number_xy>0) //FM > = 0 and not finished
{
Fm -= y1;
x0 += 1;
y0 = y0;
MotorXDriver(1,1,500); //Call the motor driver and reverse
number_xy --;
}
// down
if(Fm<0 && number_xy>0) //Fm<0
{
Fm += x1;
x0 = x0;
y0 += 1;
MotorYDriver(1,1,500); //
number_xy --;
}
if(number_xy <= 0) //
break;
if(x0 == x1 && y0 == y1)
break;
}
}
if(x1>=0&&y1<0) //The end coordinate is in the fourth quadrant (including y negative half axis and excluding x positive half axis)
{
y1= abs(y1);
number_xy = (x1+y1);
while(1)
{ //turn right
if(Fm>=0 && number_xy>0) //Fm>=0
{
Fm -= y1;
x0 += 1;
y0 = y0;
MotorXDriver(1,0,500);
number_xy --;
}
// Up
if(Fm<0 && number_xy>0) //Fm<0
{
Fm += x1;
x0 = x0;
y0 += 1;
MotorYDriver(1,1,500);
number_xy --;
}
if(number_xy <=0) //
break;
if(x0 == x1 && y0 == y1)
break;
}
}
}
//Draw arc function (inverse circle)
void DrawCricle1(int x0,int y0,int x1,int y1,u16 r ,u16 q) // Give the start point, end point coordinates, radius and quadrant position
{
//Define local variables
int x = 0,y = 0; //x. Y is the current coordinate and initialized to 0
u16 number_xy; //Define steps
number_xy = (abs(x1-x0)+abs(y1-y0));
x = abs(x0); //Record the absolute value of the current coordinate
y = abs(y0);
long Fm = 0;
Fm = x*x+y*y-r*r; //Define deviation
if(q == 1)
{
while(1) //first quadrant
{
//Arc interpolation processing, using inverse circle interpolation
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(x)+1;
x = abs(x)- 1;
y = y;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(y)+1;
x = x;
y = abs(y)+1;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 2)//Beta Quadrant
{
while(1)
{
//Arc interpolation processing, using inverse circle interpolation
if(Fm >=0 &&number_xy>0)
{
Fm = Fm - 2*abs(y)+1;
x = x;
y = abs(y)-1;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(Fm <0 &&number_xy>0)
{
Fm = Fm + 2*abs(x)+1;
x = abs(x)+1;
y = y;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 3)
{
while(1) //third quadrant
{
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(x)+1;
x = abs(x)-1;
y = y;
MotorXDriver(1,0,500);
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(y)+1;
x = x;
y = abs(y)+1;
MotorYDriver(1,1,500);
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 4)
{
while(1) //Delta Quadrant
{
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(y)+1;
y = abs(y)-1;
x = x;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(x)+1;
y = y;
x = abs(x)+1;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
}
//Draw arc function (along circle)
void DrawCricle2(int x0,int y0,int x1,int y1,u16 r ,u16 q) // Give start and end coordinates and radius
{
//Define local variables
int x = 0,y = 0; //x. Y is the current coordinate and initialized to 0
u16 number_xy; //Define steps
number_xy = (abs(x1-x0)+abs(y1-y0));
x = abs(x0); //Record the absolute value of the current coordinate
y = abs(y0);
long Fm = 0;
Fm = x*x+y*y-r*r; //Define deviation;
if(q == 1)
{
while(1) //first quadrant
{
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(y)+1;
y = abs(y)- 1;
x = x;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(x)+1;
y = y;
x = abs(x)+1;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 2)//Beta Quadrant
{
while(1)
{
if(Fm >=0 &&number_xy>0)
{
Fm = Fm - 2*abs(x)+1;
y = y;
x = abs(x)-1;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(Fm <0 &&number_xy>0)
{
Fm = Fm + 2*abs(y)+1;
y = abs(y)+1;
x = x;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 3)
{
while(1) //third quadrant
{
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(y)+1;
y = abs(y)- 1;
x = x;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(x)+1;
y = y;
x = abs(x)+1;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 4)
{
while(1) //Delta Quadrant
{
if(Fm >=0 && number_xy>0)
{
Fm = Fm - 2*abs(x)+1;
y = y;
x = abs(x)-1;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm = Fm + 2*abs(y)+1;
y = abs(y)+1;
x = x;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(x == abs(x1) &&y == abs(y1))
break;
if(number_xy <= 0) //Jump out
break;
}
}
}
Ellipse interpolation found a literature, you can refer to HowNet for details Point by point comparison oblique elliptic arc interpolation - China HowNet
The specific codes are as follows:
Ellipse interpolation
Oblique ellipse algorithm code:
#define suojian 1000000.0
#define pi 3.14159
//Draw the inverse ellipse of oblique elliptic function (including standard)
void DrawEllipse(int a,int b,int dushu,u16 q) //Give the long and short half axes, offset angle, and part
{
int xe=0;
int ye=0,xf=0,yf=0,xg=0,yg=0,xh=0,yh=0;
int x = 0,y = 0; //x. Y is the current coordinate and initialized to 0
u16 number_xy = 0; //Define steps
float sinr = sin((dushu*pi/180));
float cosr = cos((dushu*pi/180));
float A= (a*a/suojian*sinr*sinr+b*b/suojian*cosr*cosr);
float B= (a*a/suojian*cosr*cosr+b*b/suojian*sinr*sinr);
float C= (2*cosr*sinr*(b*b-a*a))/suojian;
long D = -a*a/suojian*b*b;
float E = C*C-4*A*B;
float Fm = 0;
xe =(int)(sqrt((4*B*D/suojian)/(E/suojian)));
ye =(int)((-C/(2*B))*sqrt((4*B*D/suojian)/(E/suojian))); //E-point coordinates
xf =(int)((-C/(2*A))*sqrt((4*A*D/suojian)/(E/suojian)));
yf =(int)(sqrt((4*A*D/suojian)/(E/suojian))); //F-point coordinates
xg =(int)(-sqrt((4*B*D/suojian)/(E/suojian)));
yg =(int)((C/(2*B))*sqrt((4*B*D/suojian)/(E/suojian))); // G-point coordinates
xh =(int)((C/(2*A))*sqrt((4*A*D/suojian)/(E/suojian)));
yh =(int)(-sqrt((4*A*D/suojian)/(E/suojian))); //H-point coordinates
if(q == 1)
{
number_xy = (abs(xe-xf)+abs(ye-yf));
x = xe; y = ye;
while(1) //first part
{
if(Fm >=0 && number_xy>0)
{
Fm += (-2*A/suojian*x+A/suojian-C*y/suojian);
x = x-1;
y = y;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(Fm <0&& number_xy>0)
{
Fm += (2*B/suojian*y+B/suojian+C*x/suojian);
x = x;
y = y+1;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(number_xy <= 0) //Jump out
break;
}
}
if(q == 2)
{
number_xy = (abs(xf-xg)+abs(yg-yf));
x = xf; y = yf;
while(1) // second part
{
if(Fm >=0 && number_xy>0)
{
Fm += (-2*B/suojian*y+B/suojian-C*x/suojian);
x = x;
y = y-1;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (-2*A/suojian*x+A/suojian-C*y/suojian);
x = x-1;
y = y;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(number_xy <= 0) //Jump out
break;
}
}
if(q == 3)
{
number_xy = (abs(xh-xg)+abs(yg-yh));
x = xg; y = yg;
while(1) //third part
{
if(Fm >=0 && number_xy>0)
{
Fm += (2*A/suojian*x+A/suojian+C*y/suojian);
x = x+1;
y = y;
MotorXDriver(1,0,500);
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (-2*B/suojian*y+B/suojian-C*x/suojian);
x = x;
y = y-1;
MotorYDriver(1,1,500);
number_xy --;
}
if(number_xy <= 0) //Jump out
break;
}
}
if(q == 4)
{
number_xy = (abs(xh-xe)+abs(ye-yh));
x = xh; y = yh;
while(1) //fourth part
{
if(Fm >=0 && number_xy>0)
{
Fm += (2*B/suojian*y+B/suojian+C*x/suojian);
x = x;
y = y+1;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (2*A/suojian*x+A/suojian+C*y/suojian);
x = x+1;
y = y;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(number_xy <= 0) //Jump out
break;
}
}
}
#define suojian 1000000.0
#define pi 3.14159
//Draw oblique elliptic function (including standard) along circle
void DrawEllipse1(int a,int b,int dushu,u16 q)//Give the long and short half axes, offset angle, and part
{
int xe=0;
int ye=0,xf=0,yf=0,xg=0,yg=0,xh=0,yh=0;
int x = 0,y = 0; //x. Y is the current coordinate and initialized to 0
u16 number_xy = 0; //Define steps
float sinr = sin((dushu*pi/180));
float cosr = cos((dushu*pi/180));
float A= (a*a/suojian*sinr*sinr+b*b/suojian*cosr*cosr);
float B= (a*a/suojian*cosr*cosr+b*b/suojian*sinr*sinr);
float C= (2*cosr*sinr*(b*b-a*a))/suojian;
long D = -a*a/suojian*b*b;
float E = C*C-4*A*B;
float Fm = 0;
xe =(int)(sqrt((4*B*D/suojian)/(E/suojian)));
ye =(int)((-C/(2*B))*sqrt((4*B*D/suojian)/(E/suojian))); //E-point coordinates
xf =(int)((-C/(2*A))*sqrt((4*A*D/suojian)/(E/suojian)));
yf =(int)(sqrt((4*A*D/suojian)/(E/suojian))); //F-point coordinates
xg =(int)(-sqrt((4*B*D/suojian)/(E/suojian)));
yg =(int)((C/(2*B))*sqrt((4*B*D/suojian)/(E/suojian))); // G-point coordinates
xh =(int)((C/(2*A))*sqrt((4*A*D/suojian)/(E/suojian)));
yh =(int)(-sqrt((4*A*D/suojian)/(E/suojian))); //H-point coordinates
if(q == 1)
{
number_xy = (abs(xe-xf)+abs(ye-yf));
x = xf; y = yf;
while(1) //first part
{
if(Fm >=0 && number_xy>0)
{
Fm += (-2*B/suojian*y+B/suojian-C*x/suojian);
x = x;
y = y-1;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(Fm <0&& number_xy>0)
{
Fm += (2*A/suojian*x+A/suojian+C*y/suojian);
x = x+1;
y = y;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 2)
{
number_xy = (abs(xf-xg)+abs(yg-yf));
x = xg; y = yg;
while(1) // second part
{
if(Fm >=0 && number_xy>0)
{
Fm += (2*A/suojian*x+A/suojian+C*y/suojian);
x = x+1;
y = y;
MotorXDriver(1,0,500); //right
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (2*B/suojian*y+B/suojian+C*x/suojian);
x = x;
y = y+1;
MotorYDriver(1,0,500); //up
number_xy --;
}
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 3)
{
number_xy = (abs(xh-xg)+abs(yg-yh));
x = xh; y = yh;
while(1) //third part
{
if(Fm >=0 && number_xy>0)
{
Fm += (2*B/suojian*y+B/suojian+C*x/suojian);
x = x;
y = y+1;
MotorYDriver(1,0,500);
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (-2*A/suojian*x+A/suojian-C*y/suojian);
x = x-1;
y = y;
MotorXDriver(1,1,500);
number_xy --;
}
if(number_xy <= 0) //Jump out after writing
break;
}
}
if(q == 4)
{
number_xy = (abs(xh-xe)+abs(ye-yh));
x = xe; y = ye;
while(1) //fourth part
{
if(Fm >=0 && number_xy>0)
{
Fm += (-2*A/suojian*x+A/suojian-C*y/suojian);
x = x-1;
y = y;
MotorXDriver(1,1,500); //left
number_xy --;
}
if(Fm <0 && number_xy>0)
{
Fm += (-2*B/suojian*y+B/suojian-C*x/suojian);
x = x;
y = y-1;
MotorYDriver(1,1,500); //down
number_xy --;
}
if(number_xy <= 0) //Jump out after writing
break;
}
}
}
The constant "suojian" is introduced to prevent calculation errors caused by too large data.
Since the number of steps taken by the stepping motor must be an integer, the tangent coordinate adopts forced conversion (int).
Verification of oblique ellipse algorithm in python
import math
xlist = []
ylist = []
a, b, r, x, y, s, c = 4000, 3200, 45, 0, 0, 0, 0
number_xy = 0
hudu = r * math.pi / 180.0
s = math.sin(hudu)
c = math.cos(hudu)
A = (a ** 2) * (s ** 2) + (b ** 2) * (c ** 2)
B = (a ** 2) * (c ** 2) + (b ** 2) * (s ** 2)
C = 2 * c * s * (b ** 2 - a ** 2)
D = -a * a * b * b
E = C * C - 4 * A * B
Fm = 0
xe = (int)(math.sqrt((4 * B * D) / E))
ye = (int)((-C / (2 * B)) * math.sqrt((4 * B * D) / E))
xf = (int)((-C / (2 * A)) * math.sqrt((4 * A * D) / E))
yf = (int)(math.sqrt((4 * A * D) / E))
xg = (int)(-math.sqrt((4 * B * D) / E))
yg = (int)((C / (2 * B)) * math.sqrt((4 * B * D) / E))
xh = (int)((C / (2 * A)) * math.sqrt((4 * A * D) / E))
yh = (int)(-math.sqrt((4 * A * D) / E))
number_xy = math.fabs(xf - xe) + math.fabs(yf - ye)
x, y = xe, ye
Fm = A * x * x + B * y * y + C * x * y + D
xlist.append(xe)
ylist.append(ye)
while(True):
if(Fm>=0 and number_xy>0):
Fm += -2 * A * x + A - C * y
x = x-1
y = y
number_xy -=1
xlist.append(x)
ylist.append(y)
if(Fm<0 and number_xy>0):
Fm += 2 * B * y + B + C * x
x = x
y = y + 1
number_xy -=1
xlist.append(x)
ylist.append(y)
if(x == xf and y == yf):
break
if(number_xy <=0):
break
print(xlist)
print(ylist)
str ='\n'
f=open('list2.txt','w')
f.write(str.join('%s' %id for id in xlist))
f=open('list3.txt','w')
f.write(str.join('%s' %id for id in ylist))
Matlab scatter diagram analysis
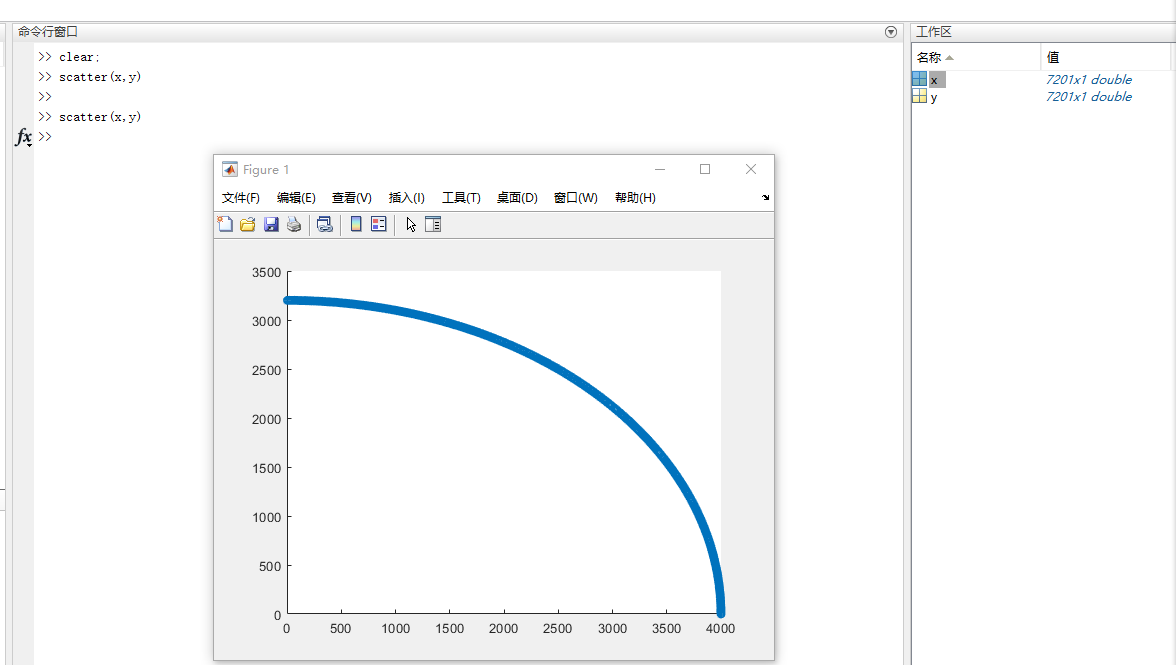Positive ellipse
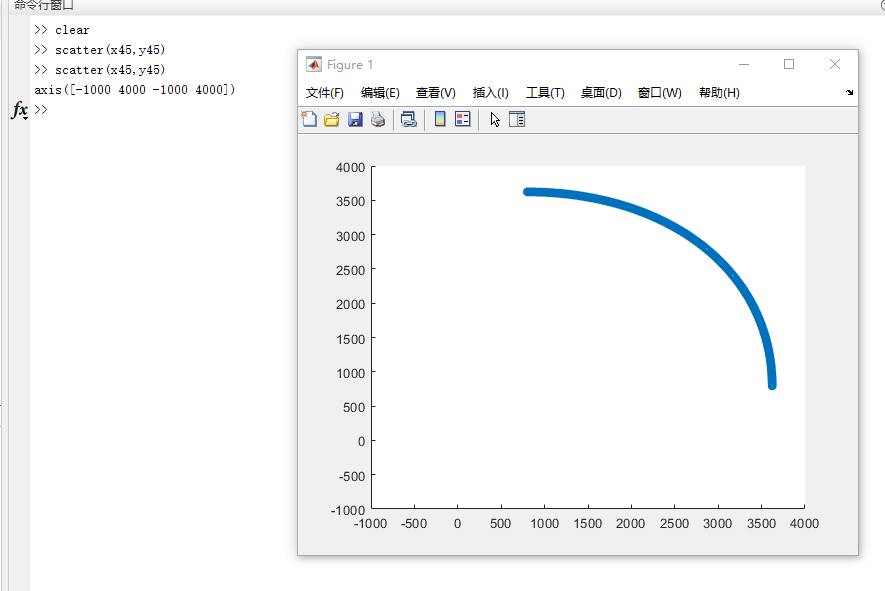
45 degree oblique ellipse
tips: when the algorithm exits, it is best to use the number of steps of the stepping motor as the exit condition. It is the most reliable.
There are still many places in the code that can be optimized, but the effect has been very good for everyone to learn and reference.