General framework

General contents:
9, Dynamic programming problem
Classical dynamic programming problem: Fibonacci sequence;
Mnemonic search: add mnemonic search on the basis of recursion; Solve problems from top to bottom.
Dynamic programming: bottom-up problem solving. Layer by layer recursion.
Think from top to bottom and solve problems from bottom to top.
Two types of dynamic return:
- One is to find the optimal solution, and the typical problem is knapsack problem; "Optimal substructure"
- The other is counting classes, which all have certain recursive properties.
The original problem is disassembled into several sub problems, and the answers of the sub problems are saved at the same time, so that each sub problem is solved only once, and finally the answer of the original problem is obtained.
1. Reference exercises
70. Climb stairs
Recursive thinking: the nth Step = one step for n-1 step + two steps for n-2 steps;
120. Triangle minimum path and
dfs ; Timeout;
Memory search; Record the minimum path.
Dynamic programming; Starting from the penultimate floor, add the younger child around him. The code is as follows: try not to modify the original array.
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<int> temp(triangle.back());
for(int i=triangle.size()-2;i>=0;i--)
for(int j=0;j<triangle[i].size();j++)
temp[j] = min(temp[j],temp[j+1])+triangle[i][j];
return temp[0];
}
};
64. Minimum path and
It is consistent with the previous question.
343. Integer split with sword finger offer to cut rope
The optimal solution of the original problem is obtained by finding the optimal solution of the subproblem.
Memory search; Yes, AC.
Dynamic programming; dp = split into these two parts, multiply directly or continue to disassemble. Take its maximum value.
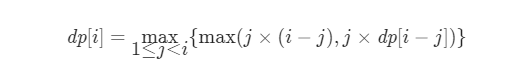
class Solution {
public:
int integerBreak(int n) {
// memo[i] represents the maximum product obtained by dividing the number I into at least two parts
vector<int> memo(n + 1, -1);
memo[1] = 1;
for(int i = 2 ; i <= n ; i ++)
// Solve memo[i]
for(int j = 1 ; j <= i - 1 ; j ++)
memo[i] = max(memo[i], max(j * (i - j), j * memo[i - j]));
return memo[n];
}
};
dfs + greed; 3 and 4 are the optimal solutions.
279. Complete square//***
The state transition equation is:
dp[i] = MIN(dp[i - j * j] + 1)
dp i is the number of squares i needs. Just enumerate j. j*j is a number, so add one, just find the minimum number of i - j*j.
91. Decoding method
Classic dynamic return questions; It is divided into two arrays, which can form a letter and can only be disassembled to form a letter.
62. Different paths 63 Different paths II
Classic dynamic return questions; Simple questions;
2. Memory search and the importance of violent exhaustion
198. House raiding
Violent exhaustion: returning to max (robbing one family, current family money + robbing the next family money) timeout; But thought is important.
In fact, all of them have been traversed. For each i, there are grabbing and not grabbing. The definition of dfs is to consider stealing index's house, not necessarily stealing the house.
int dfs(vector<int>& nums, int index)
{
if (index >= nums.size()) return 0;
return max(dfs(nums,index + 1), nums[index] + dfs(nums,index + 2));
}
int rob(vector<int>& nums) {
if (nums.size() < 2) return nums.back();
return dfs(nums, 0);
}
According to the exhaustive, plus memory search; Can pass;
int dfs(vector<int>& nums,vector<int>& memory, int index)
{
if (index >= nums.size()) return 0;
if( memory[index] != -1) return memory[index];
memory[index] = max(dfs(nums,memory,index + 1), nums[index] + dfs(nums,memory,index + 2));
return memory[index];
}
int rob(vector<int>& nums) {
if (nums.size() < 2) return nums.back();
vector<int> memory(nums.size(),-1);
return dfs(nums,memory, 0);
}
dp; Is the reverse version of memory search.
dp[i] = max(nums[i]+dp[i-2],dp[i-1]);
213. House raiding II
The core is to grab the first one or not, if you can understand the exhaustive list of the above questions; This problem is also very exhaustive. This is a case of not stealing the first one, and then stealing the first one, you can't steal the last one; Although timeout, but this idea is very important
int try_rob(vector<int>& nums,int left,int right)
{
if(left>right) return 0;
return max(try_rob(nums,left+1,right),nums[left]+try_rob(nums,left+2,right));
}
int rob(vector<int>& nums) {
if(nums.size() <2) return nums.back();
return max(try_rob(nums,1,nums.size()-1),try_rob(nums,0,nums.size()-2));
}
According to exhaustive search, plus memory search; It is found that two memories need to be used, one as the one who may have robbed the first, and the other as the one who did not.
int try_rob(vector<int>& nums,vector<int>& memory,int left,int right)
{
if(left>right) return 0;
if(memory[left] != -1) return memory[left];
memory[left] = max(try_rob(nums,memory,left+1,right),nums[left]+try_rob(nums,memory,left+2,right));
return memory[left];
}
int rob(vector<int>& nums) {
if(nums.size() <2) return nums.back();
vector<int> memory1(nums.size(),-1),memory2(nums.size(),-1);
return max(try_rob(nums,memory1,1,nums.size()-1),try_rob(nums,memory2,0,nums.size()-2));
}
dp; According to the above memory search, it is easy to think of using two DP arrays. Then take the maximum value.
int rob(vector<int>& nums) {
if(nums.size()<2) return nums.back();
vector<int>dp1(nums.size()),dp2(nums.size());
dp1[0] = nums[0];
dp1[1] = max(nums[0],nums[1]);
for(int i=2;i<nums.size()-1;i++)
dp1[i] = max(dp1[i-1],nums[i]+dp1[i-2]);
dp2[0] = 0;
dp2[1] = nums[1];
for(int i=2;i<nums.size();i++)
dp2[i] = max(dp2[i-1],nums[i]+dp2[i-2]);
return max(dp1[dp1.size()-2],dp2.back());
}
There is a question to be clear: must the i-th room be stolen under the maximum amount dp[i] of the first i-th room? Assuming that it is not stolen, the maximum value between i+1 should also be dp[i+1] = dp[i] + num? In fact, this assumption can be omitted because:
- Assuming that the i-th room is not stolen, then dp[i] = dp[i-1], dp[i+1] = dp[i] + num = dp[i-1] + num, that is, the two cases can be combined into one case;
- Assuming that the i-th room is stolen, dp[i+1] = dp[i] + num is not advisable at this time, because the i-th room cannot be stolen.
In other words, these situations have actually been taken into account. We must understand this
337. House raiding III
The core is the same as above, grab or not. The important thing is to enumerate ideas
Violent exhaustion; Although it will time out, with this foundation, it will be AC;
class Solution {
public:
int try_rob(TreeNode* root)//Trying to rob this node
{
if (!root) return 0;
int temp1 = try_rob(root->left) + try_rob(root->right);
int temp2 = root->val;
if (root->left) temp2 += try_rob(root->left->left) + try_rob(root->left->right);
if (root->right) temp2 += try_rob(root->right->left) + try_rob(root->right->right);
return max(temp1, temp2);
}
int rob(TreeNode* root) {
return try_rob(root);
}
};
Then, on the basis of exhaustive, add memorization.
class Solution {
public:
unordered_map<TreeNode*,int> memory;
int try_rob(TreeNode* root)
{
if (!root) return 0;
if( memory.find(root)!= memory.end())
return memory[root];
int temp1 = try_rob(root->left) + try_rob(root->right);
int temp2 = root->val;
if (root->left) temp2 += try_rob(root->left->left) + try_rob(root->left->right);
if (root->right) temp2 += try_rob(root->right->left) + try_rob(root->right->right);
memory[root] = max(temp1, temp2);
return memory[root];
}
int rob(TreeNode* root) {
return try_rob(root);
}
};
dp; From bottom to top, you only need to record whether the child nodes are robbed or not, and the returned results are robbed or not.
Two elements can be returned directly. The first represents stealing the node, and the second represents not stealing the node.
- Current node Grab: add the two child nodes that are not robbed;
- The current node is not robbed: take the maximum value of two child nodes that are not robbed, two child nodes that are not robbed, left node robbed + right node not robbed, left node not robbed + right node robbed; That is, return the largest child node;
class Solution {
public:
//first stole the current node, but second didn't
pair<int, int> try_rob(TreeNode* root)
{
if (!root) return make_pair(0, 0);
pair<int, int> temp_left = try_rob(root->left);
pair<int, int> temp_right = try_rob(root->right);
int temp1 = root->val;
temp1 += temp_left.second;
temp1 += temp_right.second;
int temp2 = max(temp_left.first, temp_left.second)+max(temp_right.first, temp_right.second);
return make_pair(temp1, temp2);
}
int rob(TreeNode* root) {
pair<int, int> temp = try_rob(root);
return max(temp.first, temp.second);
}
};
309. The best time to buy and sell stocks includes the freezing period//***
Violent recursion, dfs: (timeout, but important)
Just consider selling on the same day and skip directly to the day after tomorrow to continue traversal;
The maximum return of the current day is: (status is whether there are stocks)
- There are stocks: sold today, jump to the day after tomorrow to continue dfs;
- There are stocks: continue to maintain, jump to tomorrow and continue dfs;
- No stock: buy today, jump to tomorrow and continue dfs;
- No stock: no operation, skip to tomorrow to continue dfs;
Define the meaning of recursive function: for the operation of the current day, has represents whether to hold stocks on the current day;
class Solution {
public:
int dfs(vector<int>& prices,int index,bool has)
{
if(index>=prices.size() ) return 0;
int a=0;
if(has)
{
a = max(
dfs(prices,index+2,0)+prices[index],
dfs(prices,index+1,1)
);
}
else
{
a = max(
dfs(prices,index+1,1)-prices[index],
dfs(prices,index+1,0)
);
}
return a;
}
int maxProfit(vector<int>& prices) {
return dfs(prices,0,0);
}
};
Memory search: with memory, you can pass
Define a two-dimensional array to represent the maximum return of the day held or not held;
class Solution {
public:
vector<vector<int>> memory;
int dfs(vector<int>& prices,int index,bool has)
{
if(index>=prices.size() ) return 0;
int a=0;
if(has)
{
if(memory[index][1] != -1)
return memory[index][1];
a = max(
dfs(prices,index+2,0)+prices[index],
dfs(prices,index+1,1)
);
memory[index][1] = a;
}
else
{
if(memory[index][0] != -1)
return memory[index][0];
a = max(
dfs(prices,index+1,1)-prices[index],
dfs(prices,index+1,0)
);
memory[index][0] = a;
}
return a;
}
int maxProfit(vector<int>& prices) {
memory = vector<vector<int>> (prices.size(),vector<int>(2,-1));
return dfs(prices,0,0);
}
};
dp: dp represents the maximum income so far;
Three statuses: holding stock [1], not holding and just sold [2], not holding [3];
- Depends on the maximum value in ([3] - stock price of the day, [1]);
- It only depends on [1] + the stock price of the day;
- Depends on the maximum value in ([2], [3]);
Finally, the maximum value in [2] [3] is returned;
class Solution {
public:
int maxProfit(vector<int>& prices) {
//has //sold //haven't
vector<vector<int>> dp(prices.size(),vector<int>(3));
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[0][2] = 0;
for(int i=1;i<prices.size();i++)
{
dp[i][0] = max(dp[i-1][0],dp[i-1][2] -prices[i]);
dp[i][1] = dp[i-1][0]+prices[i];
dp[i][2] = max(dp[i-1][1],dp[i-1][2]);
}
return max(dp.back()[1],dp.back()[2]);
}
};
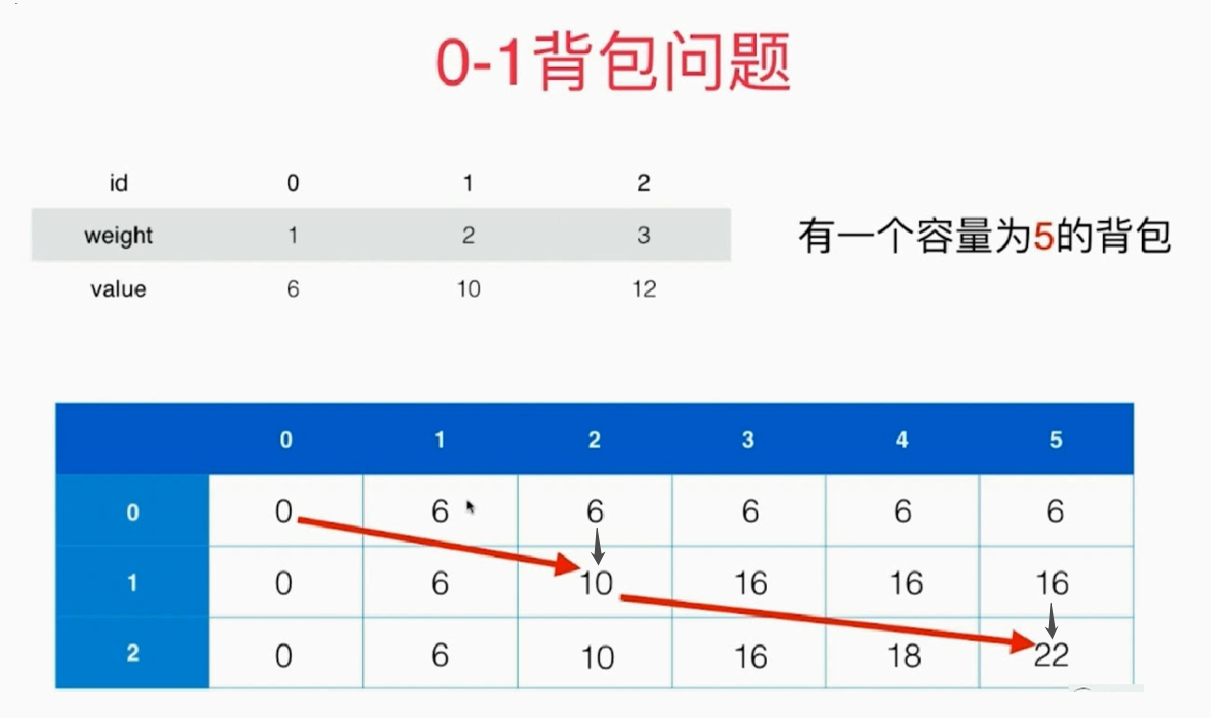
3. 0-1 knapsack problem
Backpack Capacity C (capacity), with n different item numbers 0~n-1; Weight of each article W[i], value V[i];
Q: what items are put in the backpack so that it does not exceed the volume of the backpack? On the basis of this, the total value of the items is the largest.
- Violence: O (n*2^n); We can use dfs to find overlapping subproblems, optimal substructures - > memory search and dynamic programming;
- Greedy algorithm: select according to cost performance; There is a problem of wasting space in the end; Greedy algorithm can not solve this problem;
Recursive function definition: consider putting n items into the backpack with capacity C to maximize its value.
F (i, c): take the following two maximum values;
- Don't put this item back dfs;
- Put the item, subtract the capacity, and then back dfs, return the value plus the value of the item;
Memory search:
class Knapsack0_1 {
private:
vector<vector<int>> memory;
int best_value(const vector<int> &w, const vector<int> &v, int index, int c)
{
if(index < 0 || c <= 0) return 0;
if (memory[index][c] != -1) return memory[index][c];
int res = best_value(w, v, index - 1, c);
if (c >= w[index])
res = max(res, v[index] + best_value(w, v, index - 1, c - w[index]));
memory[index][c] = res;
return res;
}
public:
int knapsack0_1(const vector<int> &w, const vector<int> &v, int c)
{
int n = w.size();
memory = vector<vector<int>>(n, vector<int>(c + 1, -1));
return best_value(w, v, n - 1, c);
}
};
Dynamic planning:
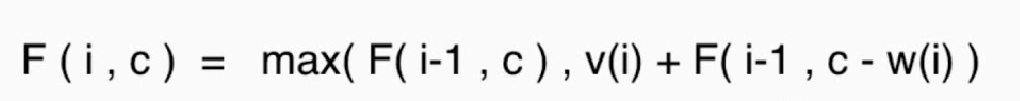

class Knapsack0_1 {
private:
public:
int knapsack0_1(const vector<int> &w, const vector<int> &v, int c)
{
assert(w.size() ==v.size());
int n = w.size();
if (n == 0) return 0;
vector<vector<int>> memory = vector<vector<int>>(n, vector<int>(c + 1, 0));
for (int j = 1; j < c + 1; j++) //capacity
if (j >= w[0]) //This item can be put in the backpack.
memory[0][j] = v[0];
//Enumeration only considers the optimal structure when the element i and the volume is j
for (int i = 1; i < n; i++)
{
for (int j = 1; j < c + 1; j++) //capacity
{
int temp = memory[i - 1][j];
if (j >= w[i]) //Current volume > = the size of the current object, consider: adding i element + the optimal solution of unexpected space except i element
temp = max(temp, v[i] + memory[i - 1][j - w[i]]);//After putting in element I, the remaining space is j - w[i]
memory[i][j] = temp;
}
}
return memory.back().back();
}
};
void main()
{
vector<int> w = { 1,2,3}, v = {6,10,12};
Knapsack0_1 k1;
cout<<k1.knapsack0_1(w,v,5);
}
According to the transfer equation, the optimal solution containing the current element is only related to the optimal solution containing the previous element.
Time O(n*c) cannot be optimized;
Space can be optimized from O(n*c) to o (2C) = O(c); It can also be optimized to O(c) as long as one line.
Optimized to 2*c space: when used inside, the index% 2 can be used.
Optimized for c space: when it is used, the current and previous are used, and there will be no conflict when updating from back to front. Update the current node directly. At the same time, when you can't update forward, you can prune and terminate in advance;
class Knapsack0_1 {
private:
public:
int knapsack0_1(const vector<int> &w, const vector<int> &v, int c)
{
assert(w.size() ==v.size());
int n = w.size();
if (n == 0) return 0;
vector<int> memory(c + 1, 0);
for (int j = 1; j < c + 1; j++) //capacity
if (j >= w[0]) //This item can be put in the backpack.
memory[j] = v[0];
//Enumeration only considers the optimal structure when the element i and the volume is j
for (int i = 1; i < n; i++)
{
for (int j = c; j >=0; j--) //capacity
{
if (j >= w[i]) //Current volume > = the size of the current object, consider: adding i element + the optimal solution of unexpected space except i element
memory[j] = max(memory[j], v[i] + memory[j - w[i]]);//After the element I is placed, the remaining space is j - w[i]
else
break;
}
}
return memory.back();
}
};
void main()
{
vector<int> w = { 1,2,3}, v = {6,10,12};
Knapsack0_1 k1;
cout<<k1.knapsack0_1(w,v,5);
}
4. 0-1 knapsack problem - variant
**Complete knapsack problem: * * each item can be used indefinitely;
- There is a maximum number of items that can be taken from each item. Expand each item to i (i is how many items can be put in this item); And converted into limited goods;
- The same as the above, but the expansion is 2 times, 4 times and 8 times of this item (the size and value are also expanded), so all combinations can be realized;
Multiple knapsack problem: each item has num[i] items; And 1 agreement;
Multidimensional cost knapsack problem: each object has both volume and weight, and knapsack also has these two dimensions;
There is one more state in dynamic programming;
The dynamic programming array becomes three-dimensional;
Constraints between goods: goods are mutually exclusive and interdependent;
5. 0-1 knapsack problem - Example
416. Segmentation and subsets//**
Typical knapsack problem: a knapsack full of sum/2; Time complexity o (nsum/2) = o (nsum)
Violent dfs: past 36 / 116;
Memory search: passed 77 / 116; Add pruning (one is satisfied, the other doesn't have to run); After that, two-dimensional arrays are faster than hash sets, but have more space.
class Solution {
public:
vector<vector<int>> my_hash;
bool fill_(vector<int>& nums, int index, int coloum)
{
if (coloum < 0 || index >= nums.size()) return false;
if (coloum == 0) return true;
if(my_hash[index][coloum]!=-1)
return my_hash[index][coloum];
bool temp;
if (nums[index] <= coloum)
temp = fill_(nums, index + 1, coloum - nums[index])||fill_(nums, index + 1, coloum);
else
temp = fill_(nums, index + 1, coloum);
my_hash[index][coloum] = temp;
return temp;
}
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto &it : nums)
sum += it;
if (sum % 2 != 0) return false;
sum >>=1;
my_hash = vector<vector<int>>(nums.size(),vector<int>(sum+1,-1));
return fill_(nums, 0, sum);
}
};
Dynamic programming: define dp [n] as the maximum capacity of a knapsack with a knapsack size of n.
Traverse nums and add a new number each time to see if the back package can be fuller. The structure of space is optimized in knapsack problem.
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto &it : nums)
sum += it;
if (sum % 2 != 0) return false;
sum >>=1;
vector<int> my_hash(sum+1,0);
for(int i=sum;i>=0&& nums[0]<=i ;i--)
my_hash[i] = nums[0];
for(int i=1;i<nums.size();i++)
{
for(int j=sum;j>=nums[i];j--)
{
if(my_hash[j-nums[i]]+nums[i]>my_hash[j])
my_hash[j] = my_hash[j-nums[i]]+nums[i];
}
if(my_hash.back() ==sum) return true;
}
return false;
}
};
Or define dp[I] as whether the backpack with size I can be filled;
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto &it : nums)
sum += it;
if (sum % 2 != 0) return false;
sum >>=1;
vector<bool> dp(sum+1);
for(int i=sum;i>=0 ;i--)
dp[i] = nums[0] ==i;
for(int i=1;i<nums.size();i++)
for(int j=sum;j>=nums[i];j--)
dp[j] = dp[j] | dp[j-nums[i]];
return dp.back();
}
};
322. Change exchange / / * combination problem?
Violent exhaustion: past 31 / 188
Memory search: too late; Note that 0 is initialized in memory. If the current path is not desirable, the same memory is changed to - 1; Otherwise, I still can't pass
class Solution {
public:
int res = INT_MAX;
vector<int> momery;
int dfs(vector<int>& coins, int amount)
{
if (amount < 0) return-1;
if (amount == 0)
return 0;
if(momery[amount]!= 0) return momery[amount];
int temp = 0,temp_res = INT_MAX;
for (int i = 0; i < coins.size(); i++)
{
temp =dfs(coins, amount - coins[i]);
if(temp !=-1)
temp_res = min(temp_res,temp+1);
}
momery[amount-1] = temp_res==INT_MAX ? -1:temp_res;
return momery[amount-1];
}
int coinChange(vector<int>& coins, int amount) {
if (amount == 0) return 0;
momery = vector<int>(amount+1,0);
return dfs(coins, amount);
}
};
Dynamic programming: dp[i] is the minimum coin combination when the total amount is I
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1,-1);
dp[0] = 0;
for (int i = 1; i <= amount; i++)
{
int temp = INT_MAX;
for (int j = 0; j < coins.size(); j++)
{
if (coins[j] <= i && dp[i - coins[j]] >= 0)
{
temp = min(temp, dp[i - coins[j]] + 1);
}
}
if (temp != INT_MAX)
dp[i] = temp;
}
return dp.back();
}
};
377. Combined total IV
It is simpler than the first two;
Violent dfs: timeout; But thought is important
class Solution {
public:
int result;
void dfs(vector<int>& nums, int target)
{
if(target<0) return ;
if(target ==0)
{
result++;
return ;
}
for(auto & it:nums)
dfs(nums,target-it);
}
int combinationSum4(vector<int>& nums, int target) {
result = 0;
dfs(nums,target);
return result;
}
};
Memory search: Yes. It's already 100%; Combinatorial problem?
Note: if temp is calculated to be 0, memory must also be overwritten; Represents that the current target cannot be filled; Otherwise, it is still overtime, which is equivalent to less pruning;
class Solution {
public:
vector<int> memory;
int dfs(vector<int>& nums, int target)
{
if(target<0) return 0;
if(target ==0) return 1;
if(memory[target]!=-1) return memory[target];
int temp =0;
for(auto & it:nums)
{
if(it<=target)
temp+=dfs(nums,target-it);
}
memory[target] =temp;
return temp;
}
int combinationSum4(vector<int>& nums, int target) {
sort(nums.rbegin(),nums.rend());
memory = vector<int>(target+1,-1);
return dfs(nums,target);
}
};
Dynamic planning: it can also be 100%;
The above memory stores the number of times the current target can be filled;
dp[I] represents the maximum number of combinations that can be filled when taget ==i;
Note: the intermediate process will overflow; The title only ensures that the final result does not overflow, which is hateful!
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<int>dp(target+1,-1);
dp[0] =1;
for(int i=1;i<target+1;i++)
{
unsigned long long temp = 0;
for(int j=0;j<nums.size();j++)
{
if(nums[j]<=i&& dp[i-nums[j]]!=-1)
temp+=dp[i-nums[j]];
}
dp[i] = temp;
}
return dp.back();
}
};
474. One and zero//***
Memory search:
At first, it was written in for or overtime;
class Solution {
public:
vector<vector<vector<int>>> memo3;
int dfs(vector<pair<int, int>> &str_num, int m, int n, int index)
{
if (index >= str_num.size() )
return 0;
if(memo3[index][m][n]!=-1) return memo3[index][m][n];
int temp = 0;
// for (int i = index; i < str_num.size(); i++)
if (m - str_num[index].first >= 0 && n - str_num[index].second >= 0)
temp = max(dfs(str_num, m, n, index + 1), 1+dfs(str_num, m - str_num[index].first, n - str_num[index].second, index + 1));
else
temp = max(temp, dfs(str_num, m, n, index + 1));
memo3[index][m][n] =temp;
return temp;
}
int findMaxForm(vector<string>& strs, int m, int n) {
vector<pair<int, int>> str_num(strs.size(), { 0,0 });
for (int i = 0; i < strs.size(); i++)
for (auto &chr : strs[i])
if (chr == '0')
str_num[i].first++;
else
str_num[i].second++;
memo3 = vector<vector<vector<int>>>(str_num.size(),vector<vector<int>>(m+1,vector<int>(n+1,-1)));
return dfs(str_num, m, n, 0);
}
};
Dynamic programming: it can be optimized into two dimensions
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<pair<int, int>> str_num(strs.size(), { 0,0 });
for (int i = 0; i < strs.size(); i++)
for (auto &chr : strs[i])
if (chr == '0')
str_num[i].first++;
else
str_num[i].second++;
vector<vector<vector<int>>> dp(str_num.size() + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
for (int k = 1; k < str_num.size() + 1; k++)
{
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <=n; j++)
{
dp[k][i][j] = dp[k-1][i][j];
if (i >= str_num[k-1].first&& j >= str_num[k-1].second)
{
dp[k][i][j] = max(dp[k][i][j], 1+dp[k-1][i - str_num[k-1].first][j - str_num[k-1].second]);
// cout<<dp[k][i][j]<<endl;
}
}
}
}
return dp.back().back().back();
}
};
139. Word splitting is simpler than the above
Complete knapsack problem; Writing dfs and memorizing search is just a way of thinking;
Violent dfs: whether the violent search vec can match the remaining ones; After 35 / 44
class Solution {
public:
bool _match(string &a,string &b,int index_a)
{
for(int i=0;i<b.size();i++)
if(a[index_a++]!=b[i]) return false;
return true;
}
bool dfs(string &s, vector<string>& wordDict,int index)
{
if(index>=s.size()) return true;
bool temp = false;
for(int i=0;i<wordDict.size();i++)
if(_match(s,wordDict[i],index))
{
temp = dfs(s,wordDict,index+wordDict[i].size());
if(temp)
break;
}
return temp;
}
bool wordBreak(string s, vector<string>& wordDict) {
return dfs(s,wordDict,0);
}
};
Memory search: the discovery status is only related to whether the current index can be matched; It's 100%
class Solution {
public:
vector<int> memo;
bool _match(string &a,string &b,int index_a)
{
for(int i=0;i<b.size();i++)
if(a[index_a++]!=b[i]) return false;
return true;
}
bool dfs(string &s, vector<string>& wordDict,int index)
{
if(index>=s.size()) return true;
if(memo[index] !=-1) return memo[index];
bool temp = false;
for(int i=0;i<wordDict.size();i++)
if(_match(s,wordDict[i],index))
{
temp = dfs(s,wordDict,index+wordDict[i].size());
if(temp)
break;
}
memo[index] = temp;
return temp;
}
bool wordBreak(string s, vector<string>& wordDict) {
memo = vector<int>(s.size()+1,-1);
return dfs(s,wordDict,0);
}
};
Dynamic planning:
dp [i] is defined as whether the s string can match from 0 to I;
Only when dp[j] matches and j~ i matches, dp[I] can match;
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> my_hash(wordDict.begin(),wordDict.end());
vector<bool> dp(s.size()+1,false);
dp[0] = true;
for(int i=1;i<s.size()+1;i++)
for(int j=i -1;j>=0;j--)
{
string temp = s.substr(j,i-j);
if(dp[j] &&my_hash.find(temp)!=my_hash.end())
{
dp[i] = true;
break;
}
}
return dp.back();
}
};
494. Goals and are relatively simple / / / * * * it's hard to think about moving back
Violence dfs: this question is very unexpected. Violence goes directly beyond... I've been blindfolded.
class Solution {
public:
int dfs(vector<int>& nums, int target,int index)
{
if(index >=nums.size())
if(target ==0) return 1;
else return 0;
int temp = 0;
temp += dfs(nums,target+nums[index],index+1);
temp += dfs(nums,target-nums[index],index+1);
return temp;
}
int findTargetSumWays(vector<int>& nums, int target) {
return dfs(nums,target,0);
}
};
Memory based search: because memory will generate negative target, use hash.
class Solution {
public:
unordered_map<int,vector<int>> memo;
int dfs(vector<int>& nums, int target,int index)
{
if(index >=nums.size())
{
if(target ==0) return 1;
else return 0;
}
if(memo.find(target)!= memo.end()&& memo[target][index]!=-1) return memo[target][index];
int temp = 0;
temp += dfs(nums,target+nums[index],index+1);
temp += dfs(nums,target-nums[index],index+1);
if(memo.find(target)== memo.end())
memo[target] = vector<int>(nums.size()+1,-1);
memo[target][index] =temp;
return temp;
}
int findTargetSumWays(vector<int>& nums, int target) {
return dfs(nums,target,0);
}
};
Dynamic return:
dp[i][j]: the number of schemes composed of j by the first I elements in the array;
Sum of all = sum; Add up = = target is preceded by the sum of symbols = neg; So sum neg neg = target;
So it is the knapsack problem of finding the combination of elements in the array to become neg; There are many pretreatment parts;
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(auto & it:nums)
sum+=it;
if((sum-target)%2!=0||(sum-target)<0) return 0;
int newt = (sum-target)/2;
vector<vector<int>> dp (nums.size()+1,vector<int>(newt+1,0));
dp[0][0] = 1;
//The number of elements that make up j in i elements
for(int i=1;i<=nums.size();i++)
{
for(int j=0;j<=newt;j++)
{
dp[i][j] = dp[i-1][j];
if(nums[i-1]<=j)
dp[i][j]+= dp[i-1][j-nums[i-1]];
}
}
return dp.back().back();
}
};
6. Longest ascending subsequence
300. Longest increasing subsequence
memo memorizes the longest increasing subsequence beginning with index;
Then the index that calls him must be strictly less than his. So only one-dimensional memory is needed; The movement is the same as the return;
376. Swing sequence
7. Longest ascending subsequence - Example
300. Longest increasing subsequence//***
Violent dfs: over 22 / 54 time complexity O (n*2^n)
class Solution {
public:
int dfs(vector<int>& nums, int index)
{
if (index >= nums.size()) return 0;
int temp = 0;
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] > nums[index])
temp = max(temp, dfs(nums, i ) + 1);
return temp;
}
int lengthOfLIS(vector<int>& nums) {
int res = 0;
for (int i = 0; i < nums.size(); i++)
res = max(dfs(nums, i) + 1, res);
return res;
}
};
Memory search: Yes
memo memorizes the longest increasing subsequence starting with index;
Then the index that calls him must be strictly less than his. So only one-dimensional memory is needed; The movement is the same as the return;
class Solution {
public:
vector<int> memo;
int dfs(vector<int>& nums, int index)
{
if (index >= nums.size()) return 0;
if(memo[index]!=-1) return memo[index];
int temp = 0;
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] > nums[index])
temp = max(temp, dfs(nums, i ) + 1);
memo[index] =temp;
return temp;
}
int lengthOfLIS(vector<int>& nums) {
int res = 0;
memo =vector<int>(nums.size()+1,-1);
for (int i = 0; i < nums.size(); i++)
res = max(dfs(nums, i) + 1, res);
return res;
}
};
Dynamic programming: O (n2)
dp[i] represents the length of the longest ascending sub sequence ending with I; This is good for analyzing problems;
So it's easy to understand; It is equivalent to the reverse of memory search memo;
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int >dp(nums.size(),1);
int _max = 1;
for(int i=1;i<nums.size();i++)
{
int temp = dp[i];
for(int j=i-1;j>=0;j--)
if(nums[j]<nums[i])
temp = max(temp,dp[j]+1);
dp[i] = temp;
_max = max(temp,_max);
}
return _max;
}
};
Dynamic return + dichotomy: this solution no longer requires the optimal solution of the problem of O (n*logn);
Consideration: the longest incremental subsequence is contained in the tail array. For each number, consider inserting it;
- If this number can be inserted, it means that this number is smaller than a number in tail, which increases the probability of longer subsequences;
- If this number cannot be inserted, it can only be placed at the end, indicating that this number is larger than the number of the longest subsequence temporarily; The longest subsequence increases; Add 1 to the longest result recorded at this time;
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int >tail(nums.size(),0);
int res = 0;
tail[res] =nums[0];
//[i,res]
for(int k=1;k<nums.size();k++)
{
auto & num = nums[k];
if(num>tail[res])
tail[++res] =num;
else
{
int i=0,j=res;
while(i<j)
{
int mid = i+(j-i)/2;
if(tail[mid]<num)
i = mid+1;
else
j=mid;
}
tail[i] = num;
}
}
return res+1;
}
};
376. Swing sequence
Violence: over 8 / 26 complexity O (n*2^n)
class Solution {
public:
int dfs(vector<int>& nums, int index, bool up)
{
if (index >= nums.size()) return 0;
int temp = 0;
if (up)
{
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] > nums[index])
temp = max(temp, dfs(nums, i, false) + 1);
}
else
{
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] < nums[index])
temp = max(temp, dfs(nums, i, true) + 1);
}
return temp;
}
int wiggleMaxLength(vector<int>& nums) {
int res = 0;
for(int i=0;i<nums.size();i++)
res = max(res, dfs(nums, 0, true) + 1);
for(int i=0;i<nums.size();i++)
res = max(res,dfs(nums,i,false)+1);
return res;
}
};
Memory search: can pass; Six percent defeat
Remember the current index and the maximum value of rising or falling;
class Solution {
public:
vector<pair<int,int>> memo;
int dfs(vector<int>& nums, int index, bool up)
{
if (index >= nums.size()) return 0;
int temp = 0;
if (up)
{
if(memo[index].first!=-1) return memo[index].first;
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] > nums[index])
temp = max(temp, dfs(nums, i, false) + 1);
memo[index].first =temp;
}
else
{
if(memo[index].second!=-1) return memo[index].second;
for (int i = index + 1; i < nums.size(); i++)
if (nums[i] < nums[index])
temp = max(temp, dfs(nums, i, true) + 1);
memo[index].second =temp;
}
return temp;
}
int wiggleMaxLength(vector<int>& nums) {
int res = 0;
memo = vector<pair<int,int>>(nums.size(),{-1,-1});
for(int i=0;i<nums.size();i++)
res = max(res, dfs(nums, 0, true) + 1);
for(int i=0;i<nums.size();i++)
res = max(res,dfs(nums,i,false)+1);
return res;
}
};
Dynamic planning:
up[i]: the longest rising swing sequence in array nums[0... I]
down[i]: the longest descending swing sequence in the array num [0... I]
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
vector<pair<int,int>> dp(nums.size(),{1,1});
for(int i=1;i<nums.size();i++)
{
if(nums[i]>nums[i-1])
dp[i] = {dp[i-1].second+1,dp[i-1].second};
else if(nums[i]<nums[i-1])
dp[i] = {dp[i-1].first,dp[i-1].first+1};
else
dp[i] =dp[i-1];
}
return max(dp.back().second,dp.back().first);
}
};
Swing + Greed: a special solution to this problem, O(n)
Because it is a swing array, directly calculate all its beats, and then calculate it according to the swing > 0 < 0;
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
for(int i=nums.size()-1;i>0;i--)
nums[i] = nums[i]-nums[i-1];
int res1 =1;
bool up = false;
for(int i=1;i<nums.size();i++)
if((up&&nums[i]>0 )||(!up &&nums[i]<0))
{
res1++;
up = !up;
}
int res2 =1;
up = true;
for(int i=1;i<nums.size();i++)
if((up&&nums[i]>0 )||(!up &&nums[i]<0))
{
res2++;
up = !up;
}
return max(res2,res1);
}
};
8. Longest common subsequence LCS
Gene matching;
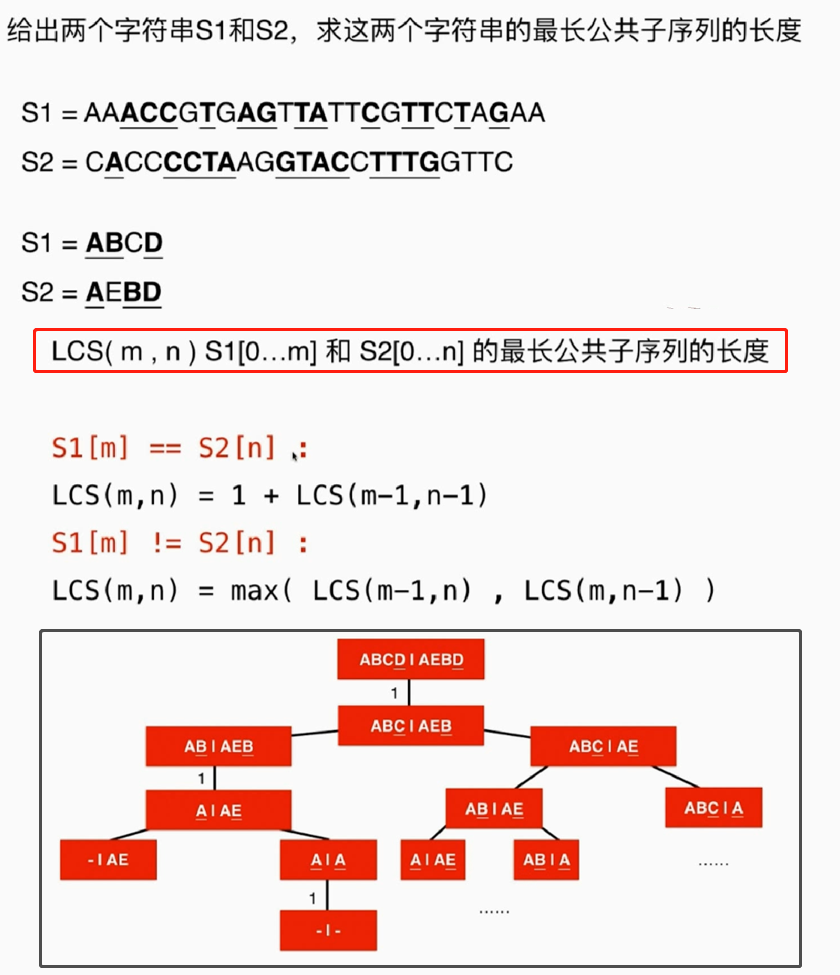

9. Dynamic programming to find out the specific solution
- Just find the solution in reverse
1. Subsequence specific solution
300. Longest increasing subsequence
You only need to select one for each length; The last one is one of the sequences

2. 0 - 1 knapsack problem specific solution
- Judge whether the current item is optimally put into the bag according to the source of the current solution;