Note: This article is after learning acwing Basic algorithm Course It is mainly used to record the template of python version algorithm.

1. Quick sort

Thought:
Divide the list with a number (pivot) in the list. The number on the left is less than pivot and the number on the right is greater than pivot.

Steps:
1. Determine pivot. Left, right, midpoint and random can be selected. There may be subtle differences in the selection of different codes. Select the midpoint here.
2. Adjust the number on the left and right sides of the pivot so that the number on the left is less than the pivot and the number on the right is greater than the pivot. Using double pointers.
3. Recursively process the left and right segments.

Template:

def quick_sort(nums, start, end):
    if start >= end:
        return
    left = start
    right = end
    
    # 1. Determine pivot. Select the midpoint here.
    mid = (left + right) // 2
    pivot = nums[mid]
    
    # 2. Adjust the number on the left and right sides of the pivot so that the number on the left is less than the pivot and the number on the right is greater than the pivot. Use double pointers.
    while left <= right:
        while left <= right and nums[left] < pivot:
            left += 1
        while left <= right and nums[right] > pivot:
            right -= 1
        if left <= right:
            nums[left], nums[right] = nums[right], nums[left]
            left += 1       # This side must be left+=1,right-=1 Otherwise, if num [left] = = num [right] = = pivot, the loop will not jump out
            right -= 1
            
    # 3. Recursively process the left and right segments.
    quick_sort(nums, start, right)
    quick_sort(nums, left, end)

2. Merge and sort

Thought:
Using the idea of divide and conquer, the list is divided into left and right parts through the midpoint in the list, and the left and right lists are sorted and merged into one list.

Steps:
1. Determine the dividing point (midpoint). mid = (l+r) // 2
2. Recursive sorting left and right >
3. Merge (merge two into one). At this time, left and right are in order. Use double pointers to compare one by one.

Template:

def merge_sort(nums):
    if len(nums) <= 1:
        return
    
    # 1. Determine the dividing point (midpoint)
    mid = len(nums) // 2
    
    # 2. Recursive sorting left and right
    L = nums[:mid]
    R = nums[mid:]
    merge_sort(L)
    merge_sort(R)
    
    # 3. Merger (two in one)
    i, j, k = 0, 0, 0
    while i < len(L) and j < len(R):
        if L[i] <= R[j]:
            nums[k] = L[i]
            i += 1
        else:
            nums[k] = R[j]
            j += 1
        k += 1
        
    while i < len(L):
        nums[k] = L[i]
        k += 1
        i += 1
    while j < len(R):
        nums[k] = R[j]
        k += 1
        j += 1

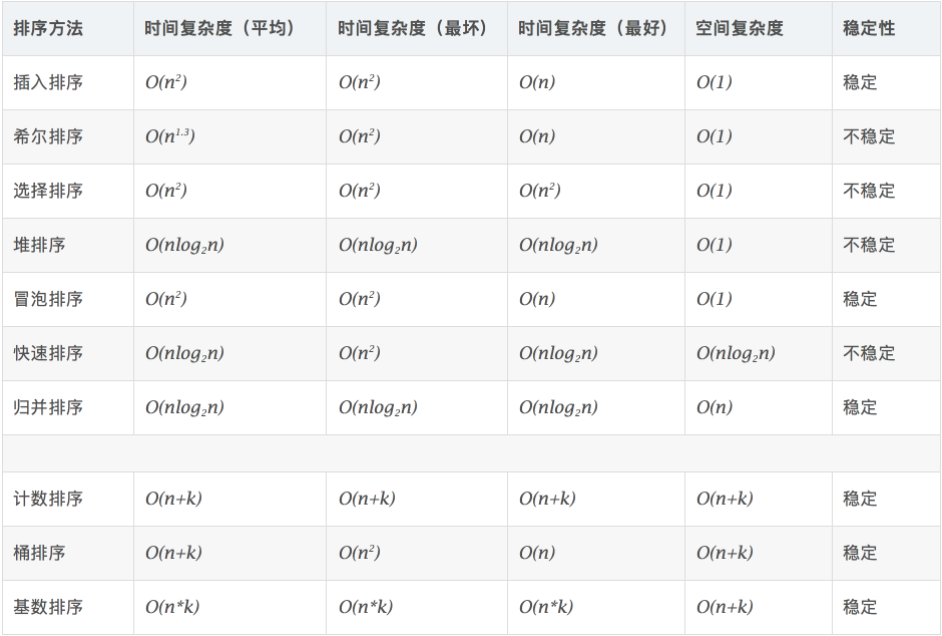
Time complexity diagram

3. Two points

Thought:
If we can find such a property and divide the whole interval into two, half satisfied and half unsatisfied, we can find the boundary point of this property.
Dichotomy and monotonicity are not equivalent. Monotonicity can be dichotomized, and dichotomization does not necessarily require monotonicity.

Steps:
1. Determine pivot. Left, right, midpoint and random can be selected. There may be subtle differences in the selection of different codes. Select the midpoint here.
2. Adjust the number on the left and right sides of the pivot so that the number on the left is less than the pivot and the number on the right is greater than the pivot. Use double pointers.
3. Recursively process the left and right segments.

Integer bisection template:
Integer dichotomy involves boundary problems, so there are two templates.

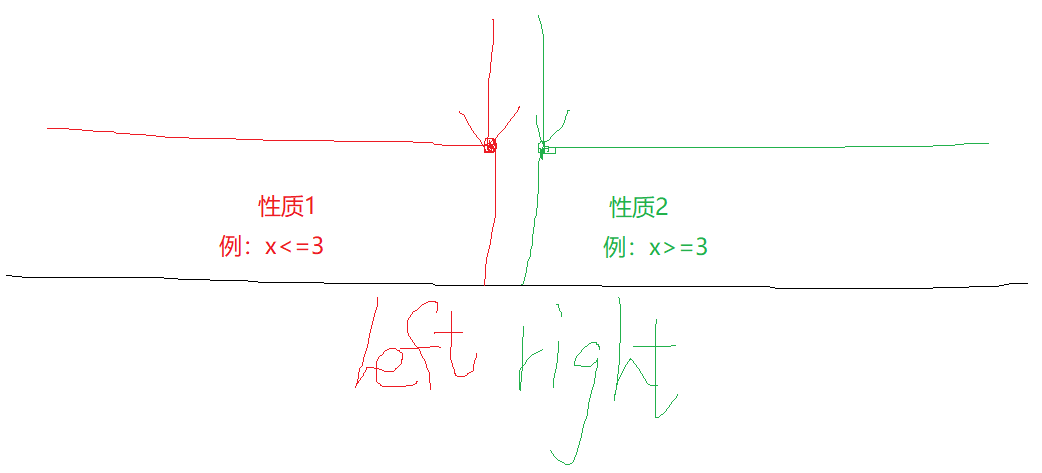
As shown in the figure above, finding left and right are two different situations. Different templates will be used when finding left and right.

def binary_search_left(nums, x):
    l = 0
    r = len(nums) - 1
    while l < r:
        mid = (l + r) // 2
        if check(mid):     # The check() function is used to check whether the left property is satisfied
            r = mid
        else:
            l = mid + 1
    else:
        return l
    
    
def binary_search_right(nums, x):
    l = 0
    r = len(nums) - 1
    while l < r:
        mid = (l + r + 1) // 2
        if check(mid):     # The check() function is used to check whether the right property is satisfied
            l = mid
        else:
            r = mid - 1
    else:
        return l

Real binary template:
Since there is no problem of rounding up or down in real number dichotomy, there is no need to discuss the boundary.

def binary_search(l, r):
    while r - l > 1e-8:      # Not necessarily 1e-8. According to the accuracy requirements, empirically, the accuracy requirements are multiplied by 1e-2
        mid = (l + r) / 2
        if pow(mid, 3) >= n:
            r = mid
        else:
            l = mid
    return l