Zuo Cheng cloud algorithm and data structure course https://www.bilibili.com/video/BV13g41157hK?p=2&spm_id_from=pageDriver

subject

Given the nodes node1 and node2 of two binary trees, find their lowest common ancestor node.

Problem solution

Solution I

Set a HashMap to save the node and its parent node (set the parent node of the root node as itself), then save all the ancestor nodes of node1 in a set set1, and seek the ancestor node of node2 to see whether it is in set1. If so, this node is the lowest common ancestor node.

//Premise: node1 and node2 must belong to the tree with head as the head
//Returns the lowest common ancestor of node1 and node2
public static Node lca(Node head, Node node1, Node node2) {
    HashMap<Node, Node> fatherMap = new HashMap<>(); //Save the node and its parent node
    fatherMap.put(head, head); //The parent node of the root node is itself
    process(head, fatherMap);  //Find the parent node of all nodes
    HashSet<Node> set1 = new HashSet<>(); //Collection of ancestor nodes of node1
    Node cur = node1;
    //Find the ancestor node of node1 and put it into set1 
    while (cur != fatherMap.get(cur)) { //Stop when tracing back to the root node
        set1.add(cur);
        cur = fatherMap.get(cur);
    }
    set1.add(head);

    //Find the ancestor node of node2
    cur = node2;
    while (!set1.contains(cur)) { //Stop when set1 contains this node
        cur = fatherMap.get(cur);
    }
    //This node is the lowest common ancestor node
    return cur;
}
//Recursively find the parent node of all nodes except the root node and save it in the fatherMap
private static void process(Node head, HashMap<Node, Node> fatherMap) {
    if (head == null) {
        return;
    }
    fatherMap.put(head.left, head);
    fatherMap.put(head.right, head);
    process(head.left, fatherMap);
    process(head.right, fatherMap);
}

Solution II

There are two situations in a binary tree:

• If one node is a descendant of another node, the lowest common ancestor node is the node that is the ancestor
• If there is no grandson relationship between the two nodes, the lowest common ancestor node is the nearest common ancestor

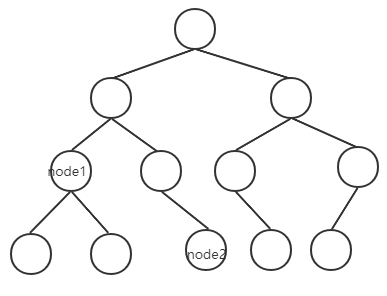
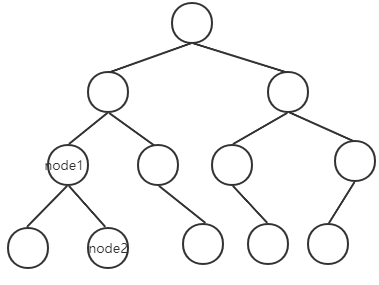
Imagine a recursive operation:

• The basic event is to return the head node of a subtree when it is null or node1 or node2.
• Recursion is performed on the left and right subtrees to obtain the return values of the left and right subtrees. There are only four possible return values of recursion: null, node1, node2, and the lowest common ancestor of the two nodes.
• When the return value of the left subtree is not empty and the return value of the right subtree is not empty (that is, the two nodes fall on the left and right subtrees respectively), the head node is returned (the head node is the lowest common ancestor node).
• When the condition that the return values of the left and right subtrees are not empty is not satisfied, if the return value of the left subtree is not empty, this value is returned (possibly node1 and node2, the lowest common ancestor node of the two nodes), otherwise, the value of the right subtree is returned (possibly null, node1 and node2, the lowest common ancestor node of the two nodes).

In this recursive operation, there are the following cases:

• If a subtree does not contain node1 and node2, the value returned by its left and right subtrees must be null, and the value returned upward must also be null; (a)

• If a subtree contains only one of node1 and node2, assuming that it contains node1, its upward return value is node1; (b)

• If a subtree contains both node1 and node2,

  • If node1 and node2 have a grandson relationship, node1 and node2 can only exist in one of the left and right subtrees of the tree. Assuming node1 is the ancestor (node1 is the lowest common ancestor node), the return values of the left and right subtrees of the tree must be node1 and null. According to the last principle of recursive operation, whether the return value of the left subtree is node1 or the right subtree is node1, Can ensure that the tree returns node1 upward.

  • If node1 and node2 have no grandson relationship and fall into their left and right subtrees respectively, according to (b), the returned values of the left and right subtrees are node1 and node2 respectively, that is, if the returned values of the left and right subtrees are not empty, the value returned upward by the subtree is the head node. (c)

  • If node1 and node2 have no grandson relationship and both fall on one of the subtrees of the tree, assuming that they fall on the right subtree, there must be such a subtree in the subtree of the right subtree that meets the above condition (c). The return value of this subtree is the head node, that is, the lowest common ancestor node, and the final return value of the right subtree is also the lowest common node. If the left subtree meets the condition (a), null is returned. Therefore, the value returned upward by the tree is the lowest common ancestor node.

Through the above analysis, we can write the following beautiful code.

public static Node lowestCommonAncestor(Node head, Node node1, Node node2) {
    if (head == null || head == node1 || head == node2) { //base case
        return head;
    }
    Node left = lowestCommonAncestor(head.left, node1, node2);
    Node right = lowestCommonAncestor(head.right, node1, node2);
    if (left != null && right != null) {
        return head;
    }
    return left != null ? left : right;
}