I Interview questions and analysis

1. Today's interview question

What search and insert algorithms do you know?

What is half search?

Talk about the code implementation of binary search method

2. Topic analysis

Today's topic is mainly to investigate our mastery of commonly used algorithms in development, especially search algorithms. For such problems, we need to understand more than remember. Although there are not many algorithms used in our projects, as a programmer, an important dimension for interviewers to measure our thinking logic is their understanding and mastery of algorithms. Especially when recruiting for large factories and junior posts, I like to investigate algorithm knowledge, such as search algorithm, insertion algorithm, etc.

So today, Yige takes the commonly used binary search as an example to explain the characteristics and usage of the algorithm.

II Reference answer

1. Common search algorithms

1.1 introduction to common search algorithms

There are four common search algorithms in Java:

1. Binary search method
2. Linear search method
3. Interpolation search method
4. Fibonacci search method

1.2 binary search method

Binary search method is a search algorithm with very high query efficiency, also known as half search method. The core idea of the algorithm is to sort the elements based on the divide and conquer strategy and constantly search in half. The time complexity is O(log2N) and the space complexity is O(1).

1.3 linear search method

It is equivalent to the circular traversal of arrays. If found, it returns the array subscript, and if not, it returns - 1. It is suitable for ordered and unordered arrays.

1.4 interpolation search method

This method is based on binary search, so that the mid value is adaptive. In the lookup table with large amount of data and uniform keyword distribution. Compared with the binary search method, the search speed of this method is faster; When the keyword distribution is uneven, this method is not necessarily better than the binary search method.

1.5 Fibonacci search method

This method first needs to calculate the golden section point, that is, first divide a line segment into two parts, so that the ratio of one part to the total length is equal to the ratio of the other part to this part, and take the approximate value of the first three digits of 0.618 (golden section ratio). Its principle is similar to the binary search method, but only changes the value of mid to make it near the golden section point, that is, mid = left +F(k-1) -1. This method is suitable for ordered array query.

2. Common sorting algorithms

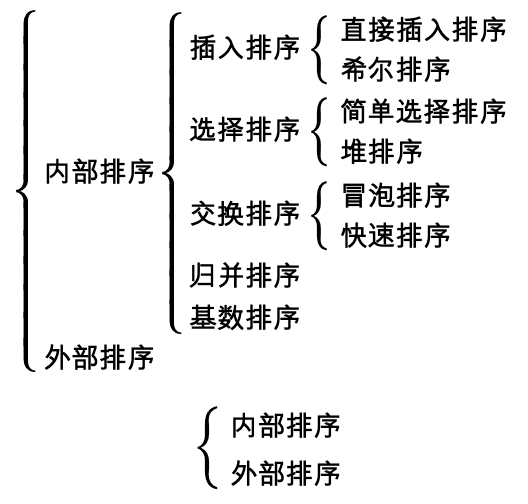
The so-called sorting is to arrange a string of records incrementally or decrementally according to the size of one or some keywords. The sorting algorithm is the method to arrange the data according to the requirements. The commonly used sorting algorithms during development are as follows:

• Direct insert sort
• Shell Sort
• Simple selection sort
• Heap sort
• Bubble sorting
• Quick sort
• Merge sort
• Radix sort

The above sorting belongs to internal sorting, that is, only the sorting algorithm with small amount of data and only memory is considered. The relationship between them is shown in the following figure:

3. Binary search method

3.1 introduction

Binary search method is a search algorithm with very high query efficiency, also known as half search method. The core idea of the algorithm is to sort the elements based on the divide and conquer strategy and constantly search in half. The time complexity is O(log2N) and the space complexity is O(1).

3.2 core ideas

In fact, the core idea of the algorithm is to adopt the divide and conquer strategy. First, the sequence to be searched is required to be orderly, and then follow the principle of reducing the search range by half every time, that is, the value in the middle of the sequence will be compared with the keyword to be searched every time. If the two are equal, the search is successful; If the value of the middle position is larger than the keyword to be checked, the search process is cycled in the first half of the sequence; If the value of the middle position is smaller than the keyword to be checked, the search process is repeated in the second half of the sequence until the required content is found. The search process of binary search method is shown in the following figure:

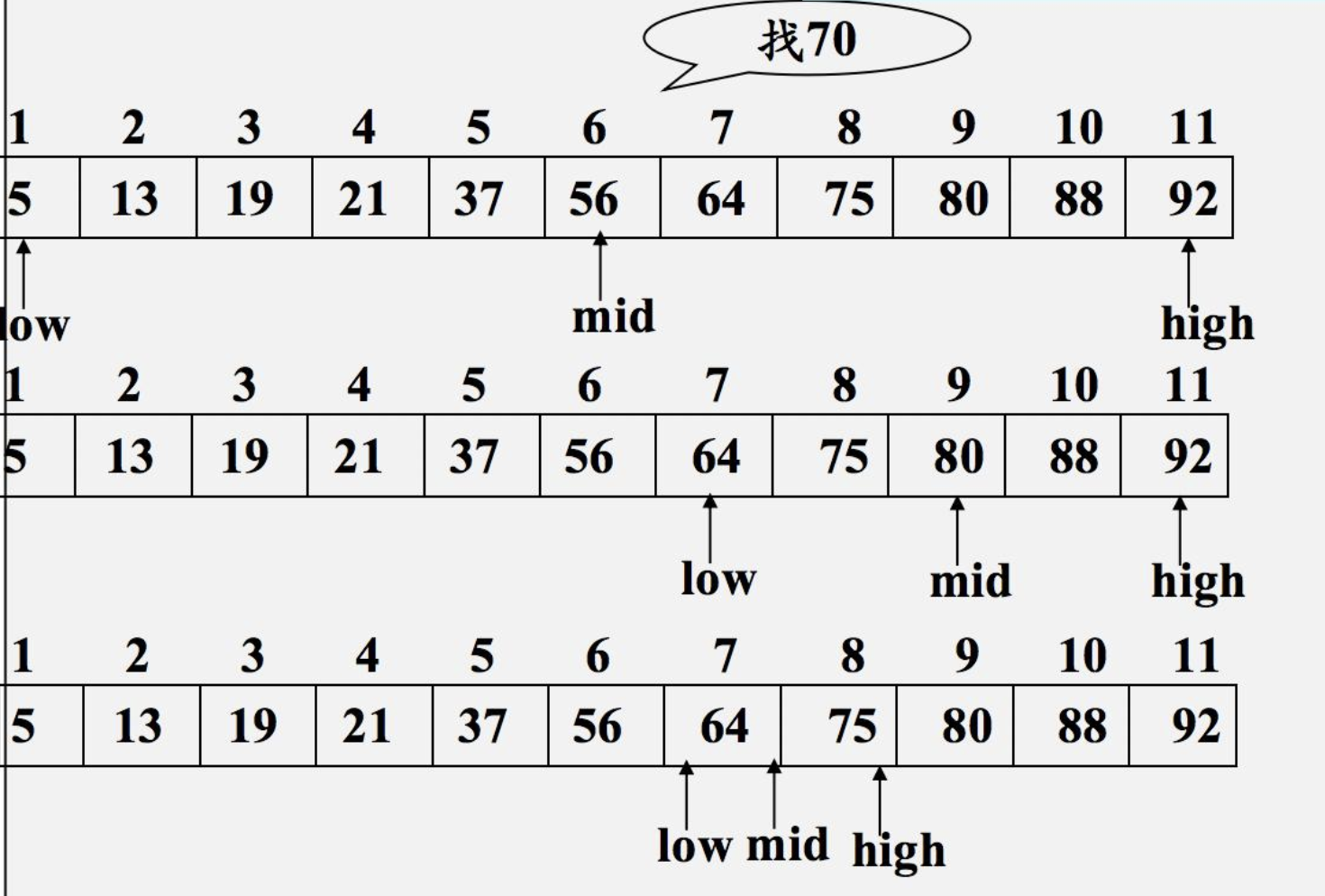
We can summarize the search process in the figure above as follows:

1. Sort the array first;
2. Calculate the middle element of the array;
3. Compare the searched key with the middle element;
4. If key = middle element, the middle index position will be returned directly;
5. If the key > middle element, it means that the key is located in the right half of the array. Repeat steps 2 to 4 in the second half (right) of the array;
6. If the key < middle element, it means that the key is in the left half of the array, so we need to repeat steps 2 to 4 in the left half.

be careful:

The sorting rules of the sequence are related to the sorting order of the array, that is, the results of sorting from large to small and from small to large are different, and the binary search method cannot be used to find out when the sequence is out of order!

In general, the process of binary search is exactly the same as that of binary search tree. If we regard a sorted array as a balanced binary search tree, the midpoint of the array is the root node of the tree, and the midpoint after halving is the root node of the next level of subtree, and so on. By constantly judging the size of the target value and the median value of each tree root node, we can decide whether the element to be found in the next step is in the left subtree or the right subtree. During code implementation, we can maintain two pointers left and right, and the range between pointers is our search range.

3.3 advantages and disadvantages

Although binary search method is an excellent search algorithm, it also has both advantages and disadvantages.

It has the advantages of less comparison times, fast search speed and good average performance;

Its disadvantage is that the table to be looked up is required to be an ordered table, and it is difficult to insert and delete.

3.4 applicable scenarios

Based on the advantages and disadvantages of binary search method, we can summarize its applicable scenarios.

The binary search method is applicable to the ordered list with frequent search but less changes, and the search sequence is required to be an ordered order structure! For example, search the sorted data in the program, especially when the storage space is compact and limited.

3.5 implementation mode

Java provides us with three specific ways to implement binary search, as follows:

1. Use iterative method;
2. Use recursive method;
3. Use arrays Binarysearch() method.

III Iterative implementation

Binary search is realized in an iterative way. The implementation idea is as follows:

First declare an array and arrange it in ascending order;

Then define the key to search;

Then calculate the median of the array and compare the key with the median;

Finally, search for the key in the left or right half of the array according to whether the key is less than or greater than the median.

Next, Yige lists the code implemented iteratively.

1. Code implementation

public class IteratorSearch {

    public static void main(String[] args) {
        //Array to be found
        int[] nums = {15, 2, 9, 3, 18, 1, 66, 20};
        //Arrange the array in ascending order first
        Arrays.sort(nums);
        System.out.println("Array sorting results:" + Arrays.toString(nums));

        //Find keyword
        int searchKey = 18;
        System.out.println("Keywords to find= " + searchKey);

        //Left boundary index
        int low = 0;
        //Right boundary index
        int high = nums.length - 1;

        // Calculate intermediate value index
        int mid = (low + high) / 2;
        //Iterative calculation of loop
        while (low <= high) {
            //If the middle value of the array is less than the search keyword, go to the right side of the array for half search
            if (nums[mid] < searchKey) {
                //Set the index of the left boundary to mid+1
                low = mid + 1;
            } else if (nums[mid] == searchKey) {
                //If the middle value of the array is equal to the keyword to be searched, it means that the content to be searched is found directly
                System.out.println("The content to be queried is located in the index[ " + mid +" ]place");
                break;
            } else {
                //If the middle value of the array is greater than the search keyword, go to the left side of the array for half search
                //At this time, set the index value of the right boundary to mid-1
                high = mid - 1;
            }
            //Constantly modify mid value
            mid = (low + high) / 2;
        }

        if (low > high) {
            System.out.println("There is nothing to find in the array!");
        }
    }

}

2. Implementation results

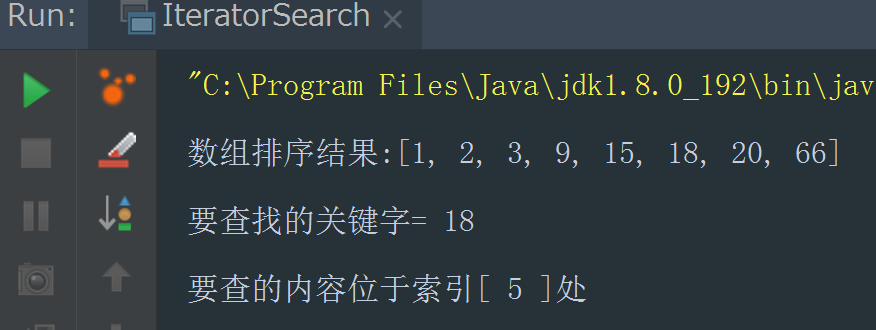
The execution results of the above code are as follows. We will find that the query keyword is successfully found.

IV Recursive implementation

The binary search method implemented recursively is relatively simple compared with the iterative method.

1. Code implementation

public class RecurrenceSearch {

    public static int binarySearch(int[] nums, int low, int high, int searchKey) {
        if (high >= low) {
            // Calculate intermediate index
            int mid = low + (high - low) / 2;
            // If the intermediate value is equal to the keyword to be searched, the index of the intermediate value is returned directly
            if (nums[mid] == searchKey) {
                return mid;
            }

            //If the middle value of the array is greater than the search keyword, go to the left side of the array for half search
            // At this time, set the index value of the right boundary to mid-1
            if (nums[mid] > searchKey) {
                //Make a recursive call to modify the value of high
                return binarySearch(nums, low, mid - 1, searchKey);
            } else {
                //If the middle value of the array is less than the search keyword, go to the right side of the array for half search, perform recursive search, and modify the value of low
                return binarySearch(nums, mid + 1, high, searchKey);
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        //Array to be found
        int[] nums = {15, 2, 9, 3, 18, 1, 66, 20};
        //Arrange the array in ascending order first
        Arrays.sort(nums);
        System.out.println("Array sorting results:" + Arrays.toString(nums));

        //Find keyword
        int searchKey = 3;
        System.out.println("Keywords to find= " + searchKey);

        int high = nums.length - 1;
        int result = binarySearch(nums, 0, high, searchKey);
        if (result == -1){
            System.out.println("There is no to find in the array key!");
        } else{
            System.out.println("The content to be queried is located in the index[ " + result +" ]place");
        }
    }

}

2. Implementation results

The execution results of the above code are as follows. We will find that the query keyword is successfully found.

V Arrays.binarySearch() method implementation

The Arrays class in Java itself provides a binarySearch() method, which can directly binary search a given array. This method will take the array and the key to be searched as parameters, and return the position of the key in the array. If the key is not found, the method will return - 1.

1. Code implementation

Arrays. The code implementation of binarysearch () is as follows. We will find that this method is very simple to implement.

public class BinarySearcher {

    public static void main(String[] args) {
        //Array to be found
        int[] nums = {15, 2, 9, 3, 18, 1, 66, 20};
        //Arrange the array in ascending order first
        Arrays.sort(nums);
        System.out.println("Array sorting results:" + Arrays.toString(nums));

        //Find keyword
        int searchKey = 3;
        System.out.println("Keywords to find= " + searchKey);

        //Directly call arrays Binary search
        int result = Arrays.binarySearch(nums, searchKey);
        if (result == -1) {
            System.out.println("There is no to find in the array key!");
        } else {
            System.out.println("The content to be queried is located in the index[ " + result + " ]place");
        }
    }

}

2. Implementation results

The execution results of the above code are as follows. We will find that the query keyword is successfully found.

Vi epilogue

How many of these algorithms have you mastered? You can leave a message to Yige in the comment area to see which algorithm knowledge you want to review.