
Hash concept
Premise:
In order structure and balance tree, there is no corresponding relationship between element key and its storage location. Therefore, when looking for an element, it must be compared many times by key. The time complexity of sequential search is O(N), and the height of the tree in the balance tree is O (log n). The efficiency of search depends on the number of comparisons of elements in the search process.
Introduction of hash:
Ideal search method: you can get the elements to be searched directly from the table at one time without any comparison. If a storage structure is constructed to establish a one-to-one mapping relationship between the storage location of an element and its key code through a function (hashFunc), the element can be found quickly through this function.
In this structure:
Insert element
According to the key of the element to be inserted, this function calculates the storage location of the element and stores it according to this location
Search element
Carry out the same calculation on the key code of the element, take the obtained function value as the storage location of the element, and compare the elements according to this location in the structure. If the key codes are equal, the search is successful. This method is called hash (hash) method. The conversion function used in hash method is called hash (hash) function, and the structure constructed is called hash table (or Hash list)
Hash Map
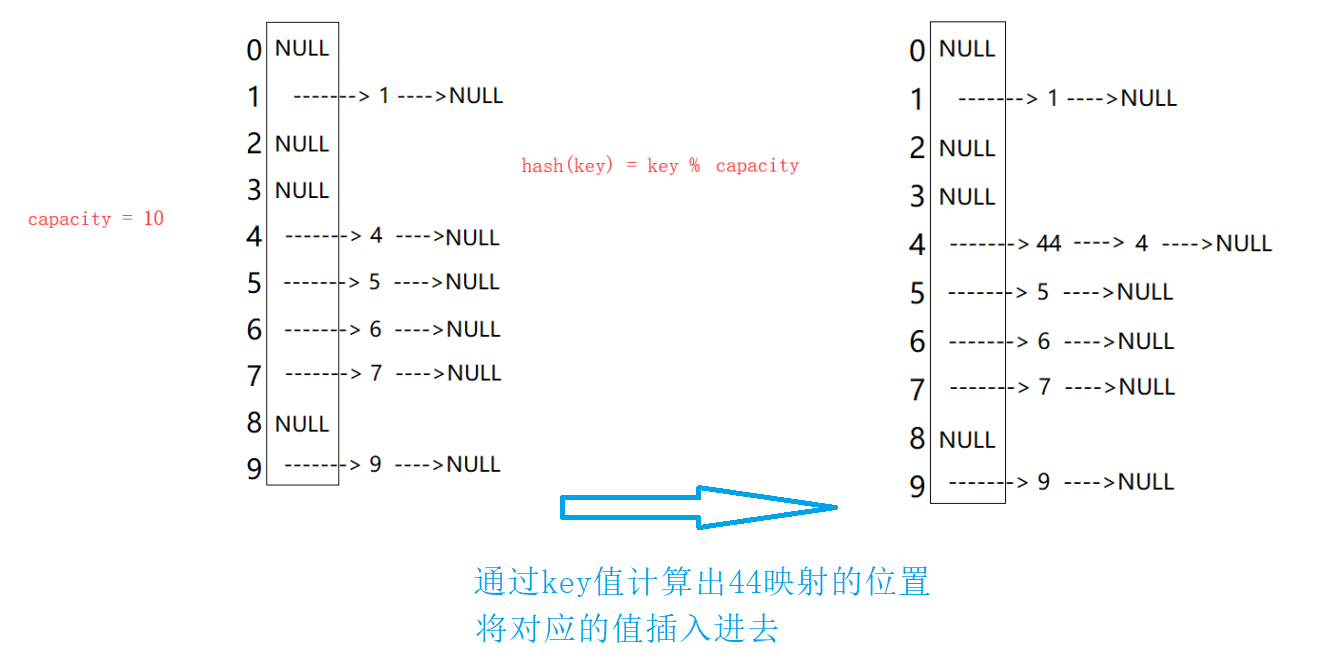
For example: data set {1, 7, 6, 4, 5, 9};
The hash function is set to: hash (key) = key% capacity; Capacity is the total size of the underlying space of the storage element.
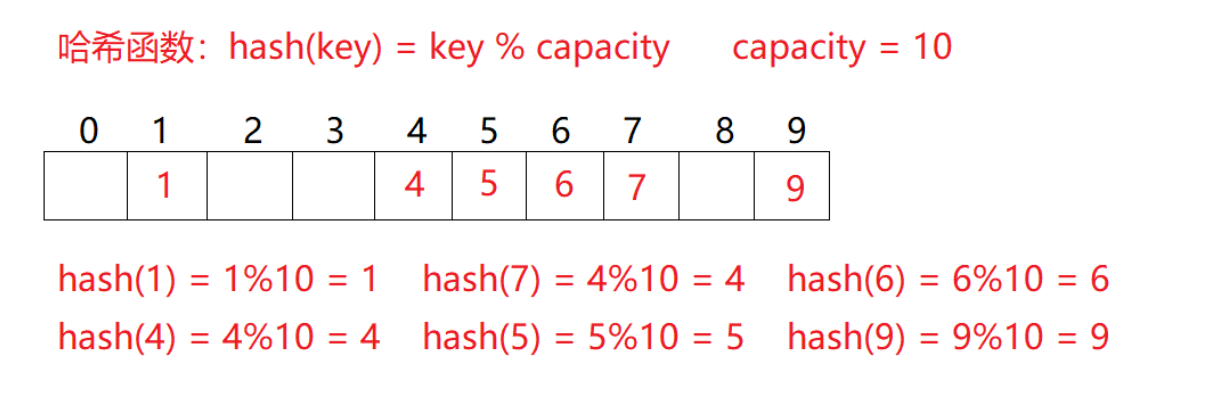
Emergence of problems
Using this method to search does not need to compare multiple key codes, so the search speed is relatively fast. Problem: according to the above hash method, inserting element 44 into the set will lead to the problem of hash conflict
Hash Collisions
For the keywords Ki and kJ (I! = J) of two data elements, there is ki= KJ, but there are: hash (KI) = = hash (kJ), that is, different keywords calculate the same hash address through the same number of hash functions. This phenomenon is called hash collision or hash collision. Data elements with different keys and the same hash address are called "synonyms". How to deal with hash conflicts?
Analyze the causes of hash conflicts
1. One reason for hash conflict may be that the hash function design is not reasonable.
2. Design principle of hash function:
-
The definition field of hash function must include all keys to be stored. If the hash table allows m addresses, its value field must be between 0 and m-1
-
The address calculated by hash function can be evenly distributed in the whole space
-
Hash functions should be simple
Common hash functions
-
Direct customization method – (commonly used, one value corresponds to one address)
Take a linear function of the keyword as the Hash address: Hash (Key) = A*Key + B advantages: simple and uniform disadvantages: you need to know the distribution of the keyword in advance. Usage scenario: it is suitable for finding small and continuous cases. It gives you a large range of data. The direct addressing method will waste a lot of space and can't deal with floating-point numbers, strings and other data -
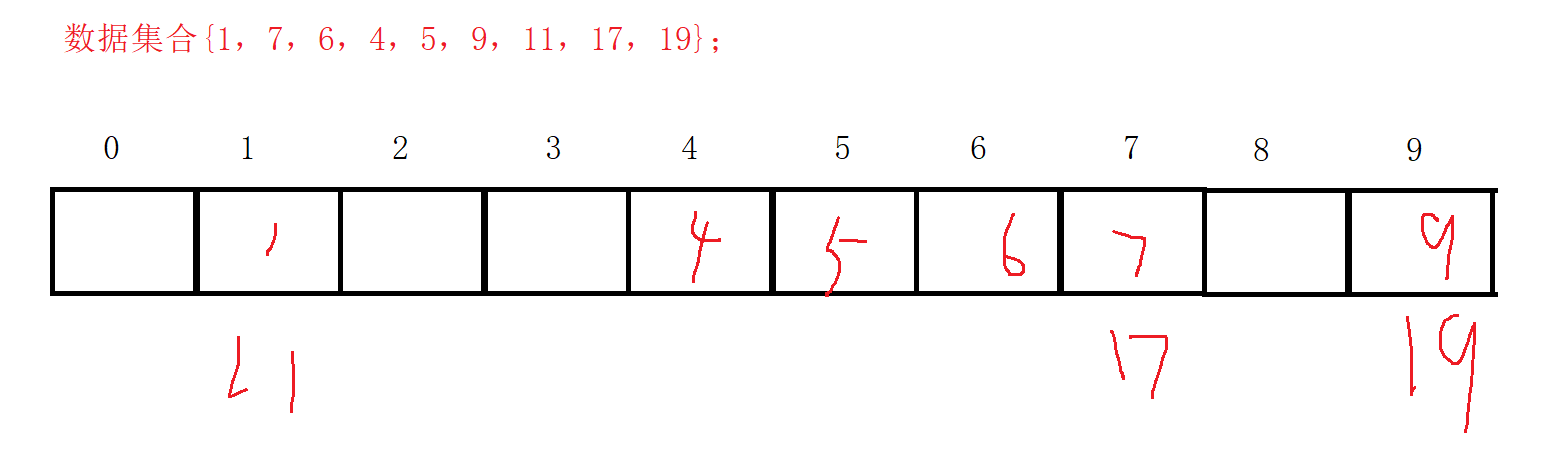
Divide and remainder method – (commonly used, it saves more space than direct addressing method, but it will cause a location to be mapped multiple times)
Let the number of addresses allowed in the hash table be m, take a prime number p not greater than m but closest to or equal to m as the divisor, and convert the key code into a hash address according to the hash function: hash (key) = key% p (p < = m)
For example: data set {1, 7, 6, 4, 5, 9, 11, 17, 19};
It can be found that the same location will be mapped twice. This phenomenon is called hash conflict
-
Square middle method – (understand)
Assuming that the keyword is 1234, its square is 1522756, and the middle three bits 227 are extracted as the hash address; For another example, if the keyword is 4321, its square is 18671041. It is more suitable to extract the middle three bits 671 (or 710) as the square median of the hash address: the distribution of keywords is not known, and the number of bits is not very large -
Folding method – (understand)
The folding method is to divide the keyword from left to right into several parts with equal digits (the digits of the last part can be shorter), then overlay and sum these parts, and take the last few digits as the hash address according to the length of the hash table. The folding method is suitable for the situation that there is no need to know the distribution of keywords in advance and there are many keywords -
Random number method – (understand)
Select a random function and take the random function value of the keyword as its hash address, that is, H(key) = random(key), where random is a random number function. This method is usually used when the keyword length is different -
Mathematical analysis – (understanding)
There are n d digits, and each bit may have r different symbols. The frequency of these r different symbols may not be the same in each bit. They may be evenly distributed in some bits, and the opportunities of each symbol are equal. They are unevenly distributed in some bits, and only some symbols often appear. According to the size of the hash table, several bits in which various symbols are evenly distributed can be selected as the hash address.
For example:

Suppose we want to store the employee registration form of a company. If we use the mobile phone number as the keyword, it is very likely that the first seven digits are the same, so we can choose the last four digits as the hash address. If such extraction is prone to conflict, we can also reverse the extracted numbers (for example, 1234 is changed to 4321), right ring displacement (for example, 1234 is changed to 4123) Left ring shift, superposition of the first two numbers and the last two numbers (for example, 1234 is changed to 12 + 34 = 46), etc.
Digital analysis method is usually suitable for dealing with the situation of large number of keywords, if the distribution of keywords is known in advance and several bits of keywords are evenly distributed
There are two common ways to resolve hash conflicts: closed hash and open hash
Closed hash closed hash: also known as open addressing method. When a hash conflict occurs, if the hash table is not full, it means that there must be an empty position in the hash table. Then you can store the key in the "next" empty position in the conflict position. So how to find the next empty location?
- Linear detection, such as the scene in 2.1, now needs to insert element 44. First calculate the hash address through the hash function. hashAddr is 44. Therefore, 44 should be inserted in this position theoretically, but the element with value 44 has been placed in this position, that is, hash conflict occurs.
- Linear detection: start from the conflicting position and detect backward in turn until the next empty position is found. Insert: obtain the position bit of the element to be inserted in the hash table through the hash function. If there is no element in the position, insert the new element directly. If there is an element hash conflict in the position, use linear detection to find the next empty position and insert the new element
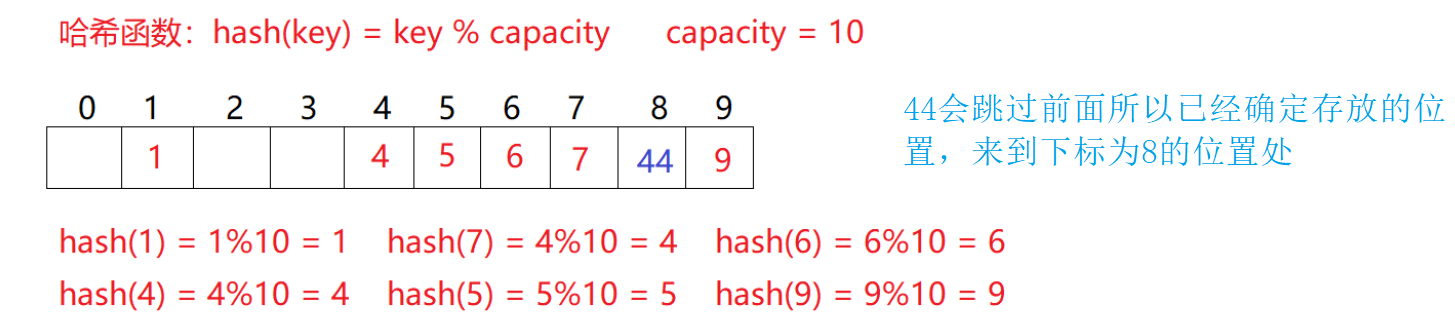
Advantages of linear detection: the implementation is very simple,
Disadvantages of linear detection: once hash conflicts occur, all conflicts are connected together, which is easy to produce data "accumulation", that is, different key codes occupy available empty positions, which makes it necessary to compare the position of a key code many times, resulting in reduced search efficiency. How to alleviate it?

Secondary detection
The defect of linear detection is that conflicting data are stacked together, which has something to do with finding the next empty position, because the way to find the empty position is to find it one by one next to each other. Therefore, in order to avoid this problem, the method to find the next empty position for secondary detection is: Hi = (H0 + I2)% m, or Hi = (H0 - i2)% m. Where: i = 1,2,3..., H0 is the position obtained by calculating the key of the element through the hash function Hash(x), and M is the size of the table. If 44 is to be inserted in 2.1, there is a conflict. The situation after use is solved as follows:
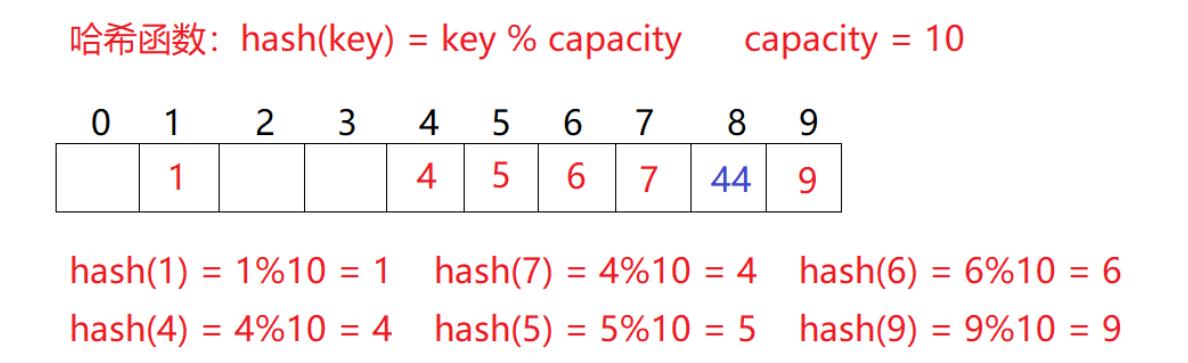
The research shows that when the length of the table is a prime number and the table loading factor A does not exceed 0.5, the new table entry can be inserted, and any position will not be explored twice. Therefore, as long as there are half empty positions in the table, there will be no problem of full table. When searching, you can not consider the situation that the table is full, but when inserting, you must ensure that the loading factor a of the table does not exceed 0.5. If it exceeds, you must consider increasing the capacity.
Therefore, the biggest defect of hash ratio is the low space utilization, which is also the defect of hash.
delete
When using closed hash to deal with hash conflicts, the existing elements in the hash table cannot be deleted physically. If the elements are deleted directly, the search of other elements will be affected. For example, if element 4 is deleted directly, 44 searching may be affected. Therefore, linear detection uses the marked pseudo deletion method to delete an element
Expansion of hash table

Summary:
1. Load factor / load factor = number of valid data stored / size of space
2. The larger the load factor, the higher the probability of conflict and the lower the efficiency of adding, deleting, checking and modifying
3. The smaller the load factor, the lower the probability of conflict, and the higher the efficiency of adding, deleting, checking and modifying. However, the space utilization is not high, and there will be a waste of space
Hash table simulation implementation
Hash table structure
namespace Hash_Tb
{
enum State
{
EMPTY,
DELETE,
EXIST
};
template<class k, class v>
struct HashData
{
public:
pair<k, v> _kv;
State _state = EMPTY;
};
//Function like class template
template<class k>
struct Hash
{
size_t& operator()(const k& key)
{
return key;
}
};
//Specialization of class template to handle the case where the key is of string type
template<>
struct Hash<string>
{
size_t operator()(const string& str)
{
size_t val = 0;
for (auto& ref : str)
{
val += ref ;
val *= 131;
}
return val;
}
};
template<class k, class v, class HashFunc = Hash<k>>
class HashTable
{
public:
private:
vector<HashData<k,v>> _table;
size_t _n = 0;
};
Hash table insert
1. Case 1: there is no data in the table, processing: resize(10)
2. Case 2: when the load factor exceeds 0.7, the hash table needs to be expanded. After the expansion of the hash table, the original value in the data set {...} has not changed, but the mapped position has changed relatively after the expansion. Therefore, it is necessary to recalculate the mapped position, and then fill the value in the set into the mapped position
3. Case 3: the space is enough and the load factor will not exceed. Insert the value normally and calculate the mapping position through the key (except the remainder method), but it is necessary to prevent hash conflict. Therefore, it is necessary to go through linear detection, find the appropriate next position, fill in the value and modify the status
4. Case 4: value redundancy, direct return
bool insert(const pair<k,v>& kv)
{
HashFunc hf;
if (Find(kv.first)) return false; //Prevent redundancy
if (_table.size() == 0) _table.resize(10); //Processing table is empty
//The load factor exceeds 0.7 and needs to be adjusted. At this time, the positions in the table are almost full
else if ((double)_n / (double)_table.size() > 0.7)
{
size_t index = 0;
HashTable<k,v> newTable; //Create a hash table
newTable._table.resize(_table.size() * 2);
//Recalculate the mapping position and copy the value into the newtable
for(size_t i = 0; i < _table.size(); i++)
{
if (_table[i]._state == EXIST)
{
newTable.insert(_table[i]._kv);
}
}
swap(newTable._table, _table);
}
else
{
//No capacity expansion is required
size_t start = hf(kv.first) % _table.size();
size_t index = start;
size_t i = 1;
while (_table[index]._state == EXIST) //If it exists
{
index = start + i * i;//Go to the position behind the secondary detection
index %= _table.size(); //Turn around
i++;
}
_table[index]._kv = kv;
_table[index]._state = EXIST;
_n++;
}
return true;
}
lookup
Search idea: by calculating the position mapped by the key value, conduct secondary detection and search at the position. If the last key value is the same, change back to the address of the position. The control on the boundary needs to be clear. When the index pointer goes to the EMPEY position, the key value you want to find will not appear again from this position, so you can directly terminate the cycle, Also as a condition of circulation
HashData<k,v>* Find(const k& key)
{
HashFunc hf;
if (_table.size() == 0) return nullptr;
size_t start = hf(key) % _table.size(); //Calculate the mapping position
size_t index = start;
size_t i = 1;
while (_table[index]._state != EMPTY) //If the EMPTY position is encountered, it means that there is no possible key value later
{
if (_table[index]._state == EXIST && _table[index]._kv.first == key) return &_table[index]; //eureka
index = start + i * i; //Walking secondary detection
index %= _table.size();
i++;
}
return nullptr; //Can't find
}
delete
When using closed hash to deal with hash conflicts, the existing elements in the hash table cannot be deleted physically. If the elements are deleted directly, the search of other elements will be affected. For example, if you delete element 44 directly, the search of element 44 may be affected. Therefore, linear detection uses the marked pseudo deletion method to delete an element
bool Erase(const k& key)
{
HashData<k, v>* ret = Find(key);
if (ret) //eureka
{
//Pseudo deletion thought
ret->_state = DELETE ,--_n; //Indicates deletion
return true;
}
else
{
return false;
}
}
Hash bucket Simulation Implementation
Introduce open hash
Open hash concept
The open hash method, also known as the chain address method (open chain method), first uses the hash function to calculate the hash address of the key code set. The key codes with the same address belong to the same subset. Each subset is called a bucket. The elements in each bucket are linked through a single linked list, and the head node of each linked list is stored in the hash table.
As can be seen from the above figure, elements with hash conflicts are placed in each bucket in the open hash
Hash bucket structure
namespace mzt
{
template <class k, class v>
struct HashNode
{
HashNode(const pair<k, v>& kv)
: _kv(kv)
, _next(nullptr)
{}
pair<k, v> _kv;
HashNode<k, v>* _next;
};
template<class k>
struct Hash
{
size_t operator()(const k& key)
{
return key;
}
};
template<>
struct Hash<string>
{
size_t operator()(const string& str)
{
size_t val = 0;
for (auto &ref : str)
{
val += ref;
val *= 131;
}
return val;
}
};
template <class k, class v, class HashFunc = Hash<k>>
class HashTable
{
typedef HashNode<k, v> Node;
public:
private:
vector<Node*> _table;
size_t _n = 0;
};
}
insert
1. Case: key value redundancy, direct return
2. When the load factor reaches 1, after the hash bucket is expanded, the original node in the bucket is removed and inserted into the new bucket. Therefore, it is necessary to traverse each bucket in the old table, judge whether there is a hanging node, define a newtable, and insert the node in the old table into the new table
3. Normal condition: calculate the mapped position through the key value, insert the knot here, and count
bool insert(const pair<k, v>& kv)
{
HashFunc hf;
if (Find(kv.first)) return false; //Prevent redundancy
else if (_n == _table.size())
{
//When the load factor of hashing reaches 1.0, it needs to be adjusted (capacity expansion + hanging node)
//Capacity expansion + take the node of the original link and hang it in the new linked list
size_t size = _table.size() == 0 ? 10 : _table.size() * 2;
vector<Node*> newtable(size, nullptr);
//Traverse the old linked list + take down the nodes of the old linked list and recalculate the position and store it in the new linked list
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
Node* copy = new Node(cur->_kv);
copy->_next = newtable[i];
newtable[i] = copy;
cur = next;
}
_table[i] = nullptr;
//After the node value in the old table is taken, empty the bucket position here
}
swap(newtable, _table); //Swap old and new tables
}
else
{
size_t index = hf(kv.first) % _table.size(); //Calculate mapping location
Node* newNoed = new Node(kv);
//Head in head
newNoed->_next = _table[index];
_table[index] = newNoed;
_n++;
}
return true;
}
lookup
Calculate the mapped position, start traversing from here, and look back until the address of the node is found. Otherwise, nullptr is returned
HashNode<k,v>* Find(const k& key)
{
HashFunc hf;
if (_table.size() == 0) return nullptr;
size_t index = hf(key) % _table.size();
Node* cur = _table[index];
while (cur)
{
if (cur->_kv.first == key) return _table[index];
cur = cur->_next;
}
return nullptr;
}
delete
Calculate the mapping position through the key value and handle it according to the delete node logic of the single linked list
bool Erase(const k& key)
{
HashFunc hf;
size_t index = hf(key) % _table.size();
Node* cur = _table[index];
Node* prev = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
if (cur == _table[index]) _table[index] = cur->_next;
else prev->_next = cur->_next;
delete cur, --_n;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
Get prime
Some materials say that the size of the hash table will reduce hash conflicts by opening the prime number. Here we implement a function to obtain the prime number, which will return the corresponding prime number according to the size of the hash table actually passed
//Get prime
size_t GetNextPrime(size_t prime)
{
const int PRIMECOUNT = 28;
//Prime sequence
const size_t primeList[PRIMECOUNT] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
size_t i = 0;
for (i = 0; i < PRIMECOUNT; i++)
{
if (primeList[i] > prime) //Find prime numbers larger than prime
return primeList[i];
}
return primeList[i];
}
Implementation of unordered series map and set simulation
unordered series associative containers
In C++98, STL provides a series of relational containers with red and black tree structure at the bottom. The query efficiency can reach (log N), that is, in the worst case, the height of red and black tree needs to be compared. When there are many nodes in the tree, the query efficiency is not ideal. The best query is that elements can be found only after a few comparisons. Therefore, in C++11, STL provides four unordered series of associative containers. These four containers are basically similar to the associative container of red black tree structure, but their underlying structure is different. In this paper, only unordered is used_ Map and unordered_set, unordered_multimap and unordered_multiset to view the document introduction
unordered_ Document introduction of map
- unordered_map is an associative container for storing < key, value > key value pairs, which allows you to quickly index their corresponding values through keys
value. - In unordered_ In a map, the key value is usually used to uniquely identify the element, while the mapping value is an object whose content is associated with the key. key
And mapped values may be of different types. - Internally, unordered_map does not sort < Kye, value > in any specific order, in order to find the key in the constant range
Corresponding value, unordered_map places key value pairs of the same hash value in the same bucket. - unordered_ The map container accesses a single element through a key faster than a map, but it is usually efficient in traversing the range iteration of a subset of elements
Lower. - unordered_maps implements the direct access operator (operator []), which allows direct access to value using key as a parameter.
- Its iterators are at least forward iterators
Hash table node structure
//key model
template <class T>
struct HashNode
{
HashNode(const T& data)
: _data(data)
, _next(nullptr)
{}
T _data;
HashNode<T>* _next;
};
Hash table transformation
template <class k, class T, class KeyOft,class HashFunc = Hash<k>>
class HashTable
{
friend struct __Iterator<k, T, KeyOft>;
typedef __Iterator<k, T, KeyOft> Iterator;
typedef HashNode<T> Node;
public:
//copy construction
HashTable(const HashTable<k, T, KeyOft>& hs)
{
HashTable<k, T, KeyOft> newtable(hs._table.size(), nullptr);
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
//Assign nodes to newtable in the way of header insertion
Node* next = cur->_next;
Node* copy = new Node(cur->_data);
copy->_next = _table[i];
_table[i] = copy;
++_n;
cur = next;
}
_table[i] = nullptr;
}
swap(newtable._table, _table);
}
//copy assignment
void operator=(const HashTable<k, T, KeyOft>& hs)
{
swap(hs._table, _table);
swap(hs._n, _n);
}
//Deconstruction
~HashTable()
{
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_table[i] = nullptr;
}
}
Iterator begin()
{
for (size_t i = 0; i < _table.size(); i++)
{
if (_table[i]) return Iterator(_table[i], this);
}
return end();
}
Iterator end()
{
return Iterator(nullptr, this);
}
//Get prime
size_t GetNextPrime(size_t prime)
{
const int PRIMECOUNT = 28;
//Prime sequence
const size_t primeList[PRIMECOUNT] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
size_t i = 0;
for (i = 0; i < PRIMECOUNT; i++)
{
if (primeList[i] > prime)
return primeList[i];
}
return primeList[i];
}
pair<Iterator, bool> insert(const T& x)
{
KeyOft kf;
HashFunc hf;
if (Find(kf(x))._node)
{
return make_pair(Find(kf(x)), false); //Prevent redundancy
}
else if (_n == _table.size())
{
//When the load factor of hashing reaches 1.0, it needs to be adjusted (capacity expansion + hanging node)
//Capacity expansion + take the node of the original link and hang it in the new linked list
size_t size = GetNextPrime(_table.size());
vector<Node*> newtable(size, nullptr);
//Traverse the old linked list + take down the nodes of the old linked list and recalculate the position and store it in the new linked list
for (size_t i = 0; i < _table.size(); i++)
{
Node* cur = _table[i];
while (cur)
{
Node* next = cur->_next;
Node* copy = new Node(cur->_data);
copy->_next = newtable[i];
newtable[i] = copy;
cur = next;
}
_table[i] = nullptr;
}
swap(newtable, _table);
}
size_t index = hf(kf(x)) % _table.size(); //Calculate mapping location
Node* newNoed = new Node(x);
//Head in head
newNoed->_next = _table[index];
_table[index] = newNoed;
_n++;
return make_pair(Iterator(_table[index], this),true); //Returns the pair structure of the inserted node and true
}
Iterator Find(const k& key)
{
KeyOft kf;
HashFunc hf;
if (_table.size() == 0) return Iterator(nullptr, this);
size_t index = hf(key) % _table.size();
Node* cur = _table[index];
while (cur)
{
if (kf(cur->_data) == key) return Iterator(cur,this);
cur = cur->_next;
}
return Iterator(nullptr, this);
}
bool Erase(const k& key)
{
HashFunc hf;
KeyOft kf;
size_t index = hf(key) % _table.size();
Node* cur = _table[index];
Node* prev = nullptr;
while (cur)
{
if (kf(cur->_data) == key)
{
if (cur == _table[index]) _table[index] = cur->_next;
else prev->_next = cur->_next;
delete cur, --_n;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
private:
vector<Node*> _table;
size_t _n = 0;
};
Hash table iterator
//forward declaration
template <class k, class T, class KeyOft, class HashFunc> class HashTable;
//Iterator for hash table
template <class k, class T, class KeyOft, class HashFunc = Hash<k>>
struct __Iterator
{
typedef HashTable<k, T, KeyOft, HashFunc> Ht;
typedef __Iterator<k, T, KeyOft> Self;
typedef HashNode<T> Node;
Node* _node; //Record the location of the node
Ht* _pht; //Address where hash table is stored
__Iterator(Node* node, Ht *pht) //Constructor
:_node(node)
,_pht(pht)
{ }
Self& operator++()
{
if (_node->_next) //> 1 node left in the current bucket
{
_node = _node->_next;
}
else // //There is only one node left in the current bucket. You need to find the next bucket and change the location of the bucket_ Assign node to this node
{
//Use anonymous objects
size_t index = HashFunc() (KeyOft() (_node->_data)) % _pht->_table.size();//Calculate current position
index++; //Find from the next location in the current location
while (index < _pht->_table.size())
{
if (_pht->_table[index]) //Find the position of the next bucket and assign the value to_ node
{
_node = _pht->_table[index]; //Assign the head node of the bucket at this position to_ node
return *this;
}
index++;
}
_node = nullptr;
}
//This position indicates that the traversal has been completed
return *this;
}
//The following are simple interfaces, and the focus is still the pre + + operator
T& operator*() {return _node->_data;}
T* operator->() {return &_node->_data;}
bool operator!=(const Self& node)const { return _node != node._node; }
bool operator==(Self& node)const { return _node == node._node; }
};
unordered_map simulation
namespace mzt
{
template<class k, class v>
class unoddered_map
{
struct MapKeyOft
{
k operator()(const pair<k, v>& key)
{
return key.first;
}
};
public:
typedef typename mzt::__Iterator<k, pair<k,v>, MapKeyOft> Iterator;
Iterator begin() { return _hstable.begin(); }
Iterator end() { return _hstable.end(); }
pair<Iterator, bool> insert(const pair<k, v>& kv)
{
return _hstable.insert(kv);
}
private:
mzt::HashTable<k, pair<k, v>, MapKeyOft> _hstable;
};
void map_test()
{
int a[] = {1,4,5,78,56,6,3,4,11,21,30};
unoddered_map<int, int> mp;
for (auto& ref : a) mp.insert(make_pair(ref,ref));
unoddered_map<int,int>::Iterator it = mp.begin();
while (it != mp.end())
{
cout << it->first << " ";
++it;
}
}
}
unordered_set simulation
namespace mzt
{
template<class k>
class unordered_set
{
struct SetKeyOft
{
k operator()(const k& key)
{
return key;
}
};
public:
typedef typename mzt::__Iterator<k, k, SetKeyOft> Iterator;
Iterator begin() { return _hstable.begin(); }
Iterator end() { return _hstable.end(); }
pair<Iterator, bool> insert(const k& kv)
{
return _hstable.insert(kv);
}
private:
mzt::HashTable<k, k, SetKeyOft> _hstable;
};
void set_test()
{
int a[] = { 1,4,5,78,56,6,3,4,11,21,30 };
unordered_set<int> s;
for (auto& ref : a) s.insert(ref);
unordered_set<int>::Iterator it = s.begin();
while (it != s.end())
{
cout << *it<< " ";
++it;
}
}
}
