I was brushing the water question, but I suddenly found this question. It happened to be what we learned yesterday, so we came to consolidate it.

Give it to us n n n points, m m m edges. Each edge has a length. Let's find the shortest path from 1 to each point.

Idea: the weight of this problem (i.e. path) is greater than or equal to 1 1 1, so you can use Dijkstra to solve this problem. (because I only learned this algorithm for the time being) I was afraid of the data point card, so I fought with the topic and added heap optimization. This is also a classic SSSP topic (single source shortest path problem), which is worth brushing. There are several approaches to this topic:

1.Dijkstra algorithm.

2. Dijkstra with priority queue.

3. Bellman Ford algorithm

4.SPFA

Next, let's introduce Dijkstra. Dijkstra algorithm is a typical single source shortest path algorithm, which is used to calculate the shortest path from one node to all other nodes. The main feature is to take the starting point as the center and expand outward layer by layer until it reaches the end point.

Algorithm idea: Set G = ( V , E ) G=(V,E) G=(V,E) is a weighted directed graph, which sets the vertices in the graph V V V is divided into two groups. The first group is the vertex set with the shortest path S S S means, initially S S There is only one source point in S. after that, each shortest path will be added to the set S S S until all vertices are added to S S In S, the algorithm ends), and the second group is the vertex set of the remaining undetermined shortest path (with U U U), add the vertices of the second group in the order of increasing the length of the shortest path S S S. In the process of joining, always keep from the source point v v v to S S The shortest path length of each vertex in S shall not be greater than that from the source point v v v to U U The shortest path length of any vertex in U. In addition, each vertex corresponds to a distance, S S The distance between the vertices in S is from v v v the shortest path length to this vertex, U U The distance between the vertices in U is from v v v this vertex includes only S S The vertex in S is the current shortest path length of the middle vertex.
The time complexity of ordinary Dijkstra is O ( n 2 ) O(n^2) O(n2), since the author may have bad intentions, we use heap optimization. Time complexity only needs O ( ( n + m ) ∗ l o g m ) O((n + m) * log m) O((n+m)∗logm).

Algorithm proof:

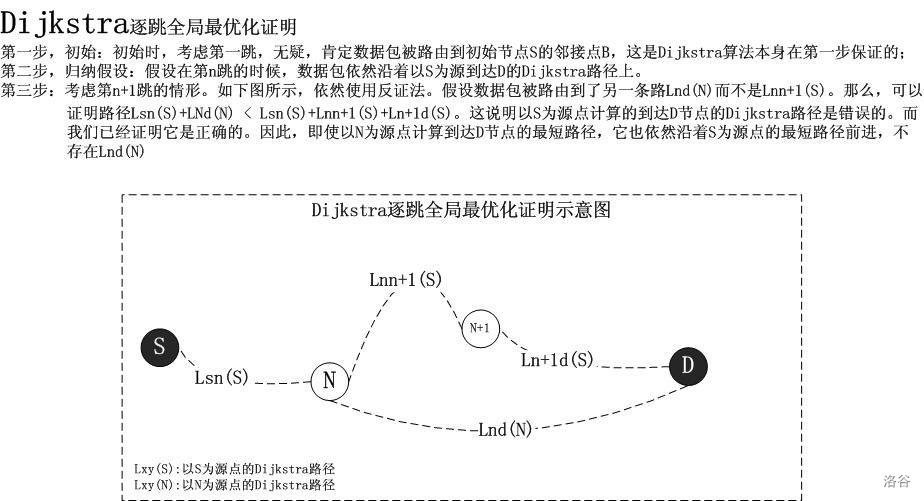
Code analysis: first input all those paths, and then use Chained forward star map.

int cnt,z[1000001],qz[1000001],next[1000001],f[100001];
void add(int a,int b,int c){
	cnt++;
	z[cnt] = b;
	qz[cnt] = c;
	next[cnt] = f[a];
	f[a] = cnt;
}

After that is the Dijkstra section

for(int i = 1;i <= n;i++){
	d[i] = inf;//Initialization, let d[1] = 0
}
d[1] = 0;
q.push(make_pair(0,1));Adopted here C++Written with binary. Note 2* 
while(q.size()){//When there are elements in the heap 
	int x = q.top().second;
	q.pop();//Delete after fetching 
	if(visited[x]){//Judge whether there is any process
		continue;
	}
	visited[x] = 1;//Mark it as passing
	for(int i = f[x];i;i = next[i]){
		if(d[z[i]] > d[x] + qz[i]){//dijkstra algorithm core statement 
			d[z[i]] = d[x] + qz[i];//replace
			q.push(make_pair(d[z[i]],z[i]));//Each time the relaxation succeeds, the information about the current point is pushed into the heap.
		}
	}
}
Note 2: C++Self contained binary pair,The definition method is pair<(Data type 1),(Data type 2)>(name). It is equivalent to a structure containing two variables. pair Used by two members in.first and.second Visit. In the priority queue, pair So first For the first keyword, with second Sort for the second keyword. towards pair The inserted element can be directly assigned as a structure, or it can be used make_pair()Insert. 

Full code:

#include<bits/stdc++.h>
using namespace std;
const int inf = 2147483647;
priority_queue <pair<int,int>,vector<pair<int,int> //Definition method of STL priority queue (in case of pair). Because of the small root heap, it needs to be defined like this. Note * >, greater < pair < int, int > > > Q;
int n,m,s,u,v,w;
long long z[1000001],qz[1000001],cnt,d[10000001],next[10000001],f[10000001];
bool visited[1000001];
void add(int a,int b,int c){//Chained forward star map
	cnt++;
	z[cnt] = b;
	qz[cnt] = c;
	next[cnt] = f[a];
	f[a] = cnt;
}
int main(){
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		cin >> u >> v >> w;
		add(u,v,w);
	}
	for(int i = 1;i <= n;i++){
		d[i] = inf;
	}
	d[1] = 0;//Initialize dis array
	q.push(make_pair(0,1));//It is written in C + + with binary. Note 2*
	while(q.size()){ 
		int x = q.top().second;//q.top() takes out the top of the heap, that is, the point closest to the starting point.
		q.pop();//Delete after fetching 
		if(visited[x]){
			continue;
		}
		visited[x] = 1;
		for(int i = f[x];i;i = next[i]){
			if(d[z[i]] > d[x] + qz[i]){
				d[z[i]] = d[x] + qz[i];
				q.push(make_pair(d[z[i]],z[i]));
			}
		}
	}
	for(int i = 1;i <= n;i++){
		if(d[i] == 2147483647){
			cout << "-1 ";
			continue;
		}
		cout << d[i] << " ";
	}
	return 0;
}
Note: priority_queue<(data type)>The default definition method of is large root heap. only priority_queue<(data type),vector<(data type)>,greater<(data type)> >To define a small root heap. In addition, you should separate two connected angle brackets with spaces(<<or>>)，Otherwise, the compiler recognizes it as a stream read operator.
 	Of course, you can also choose overloaded operators, but I think it's better. After all, many people can't overload.
 	In addition, although the priority queue is equivalent to the heap, the internal principle is realized by giving a priority value to the variable, which is different from the heap.
Note 2: C++Self contained binary pair,The definition method is pair<(Data type 1),(Data type 2)>(name). It is equivalent to a structure containing two variables. pair Used by two members in.first and.second Visit. In the priority queue, pair So first For the first keyword, with second Sort for the second keyword. towards pair The inserted element can be directly assigned as a structure, or it can be used make_pair()Insert. 

The idea comes from Ophelia's P3371 blog.

Konjaku's code, if there is any deficiency, please ask the boss for advice.