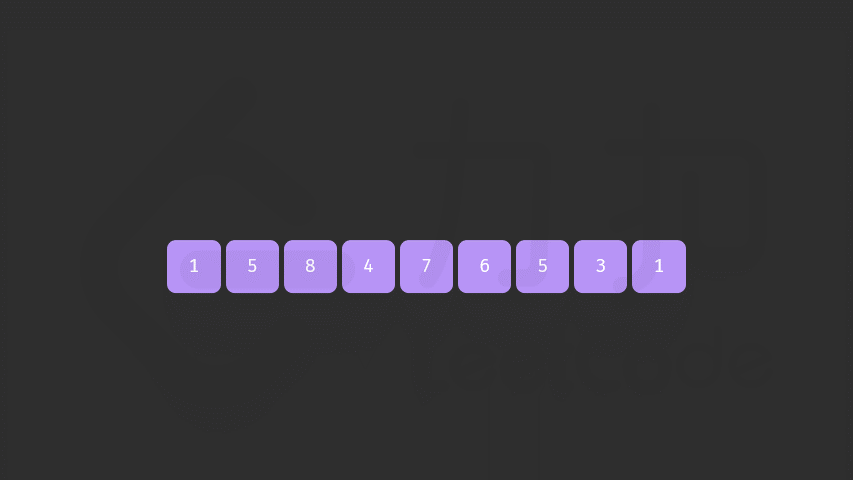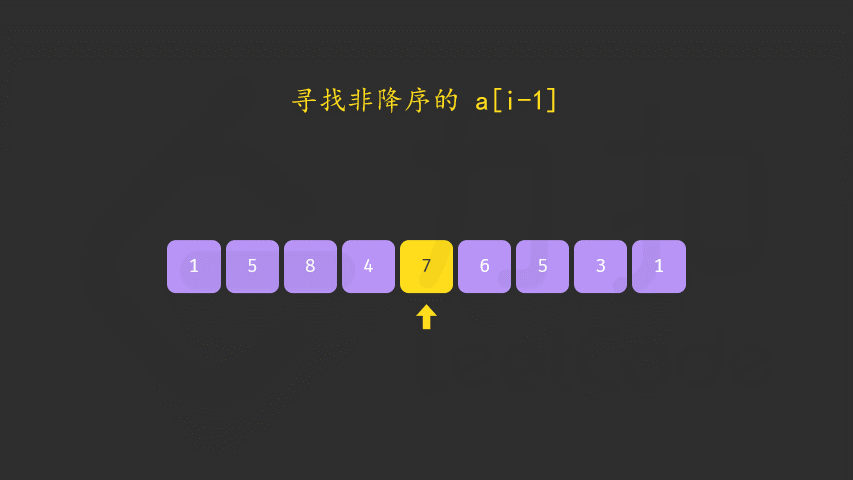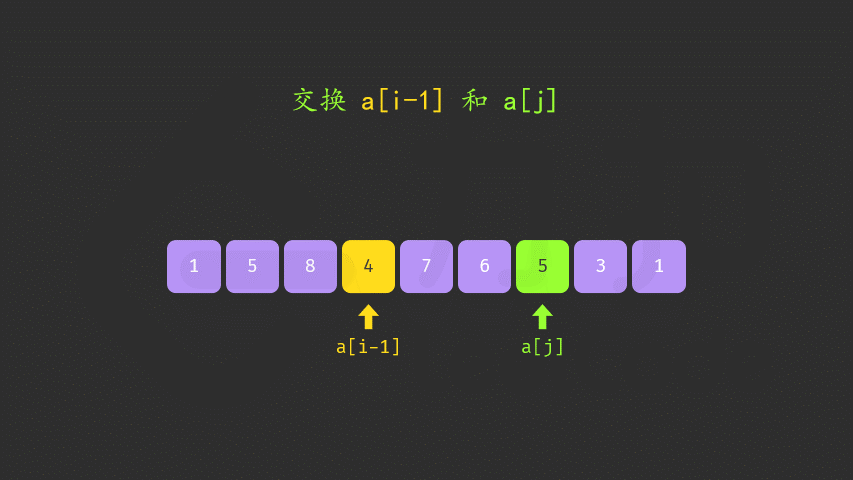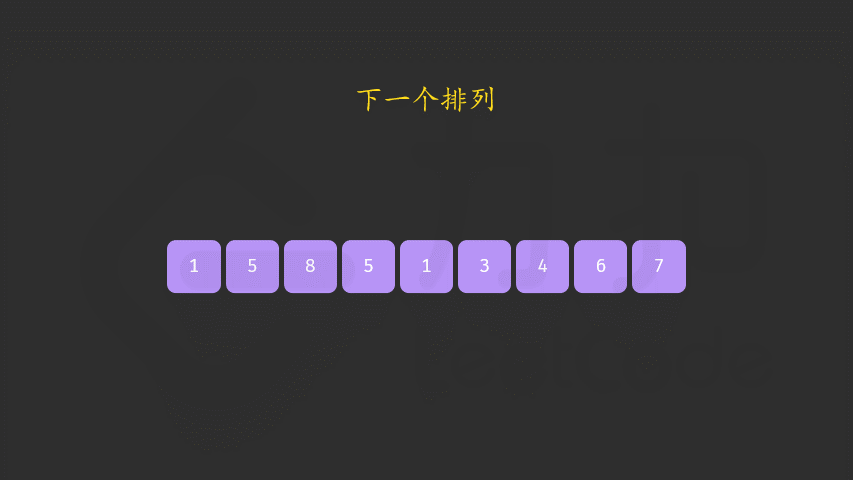1, Title Requirements

• An arrangement of an integer array is to arrange all its members in sequence or linear order.
• For example, arr = [1,2,3], the following can be regarded as the arrangement of arr: [1,2,3], [1,3,2], [3,1,2], [2,3,1].
• The next permutation of an array of integers refers to the next lexicographically ordered permutation of its integers. More formally, if all permutations of an array are arranged in a container from small to large according to their dictionary order, the next permutation of the array is the one behind it in the ordered container. If there is no next larger permutation, the array must be rearranged to the least lexicographically ordered permutation (that is, its elements are arranged in ascending order).
• • For example, the next permutation of arr = [1,2,3] is [1,3,2].
• • Similarly, the next permutation of arr = [2,3,1] is [3,1,2].
• • The next permutation of arr = [3,2,1] is [1,2,3], because there is no permutation with larger dictionary order in [3,2,1].
• Give you an integer array nums and find the next arrangement of nums.
• It must be modified in place and only additional constant space is allowed.
• Example 1:

Input: nums = [1,2,3]
Output:[1,3,2]

• Example 2:

Input: nums = [3,2,1]
Output:[1,2,3]

• Example 3:

Input: nums = [1,1,5]
Output:[1,5,1]

• Tips:
• • 1 <= nums.length <= 100
• • 0 <= nums[i] <= 100

2, Train of thought analysis

• "Next permutation" is defined as the next larger permutation in the dictionary order of a given number sequence. If there is no next larger arrangement, rearrange the numbers into the smallest arrangement (i.e. ascending arrangement). We can formally describe the problem as: given several numbers, we can combine them into an integer. How to rearrange these numbers to get the next larger integer. If there is no larger integer, the smallest integer is output.
• The problem requires an algorithm to rearrange the given number sequence into the next larger arrangement in the dictionary order. Take the numerical sequence [1,2,3] as an example. According to the dictionary order, its arrangement is: [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]. In this way, the next arrangement of [2,3,1] is [3,1,2]. In particular, the next arrangement of the largest arrangement [3,2,1] is the smallest arrangement [1,2,3]. So, how to get such an order?
• • We hope that the next number is larger than the current number, so as to meet the definition of "next arrangement". Therefore, you only need to exchange the following "large number" with the preceding "decimal" to get a larger number. For example, 123456, a larger number 123465 can be obtained by exchanging 5 and 6.
• • It is also hoped that the increase of the next number will be as small as possible, so as to meet the requirement of "the next arrangement is close to the current arrangement". In order to meet this requirement, you need to:
• • • Exchange in the low position to the right as far as possible, and you need to find it from the back to the front;
• • • Exchange a "large number" as small as possible with the preceding "decimal". For example, 123465, the next arrangement should exchange 5 and 4 instead of 6 and 4;
• • • After changing the "large number" to the front, you need to reset all the numbers after the "large number" to ascending order. The ascending order is the smallest order. Take 123465 as an example: first, exchange 5 and 4 according to the previous step to obtain 123564; Then you need to reset the numbers after 5 to ascending order to get 123546. Obviously, 123546 is smaller than 123564, and 123546 is the next arrangement of 123465.

3, Solving algorithm

① Two scans

• Note that the next spread is always larger than the current spread, unless it is already the largest spread. We hope to find a way to find a new sequence larger than the current sequence, and the magnitude of the increase is as small as possible. Specifically:
• • You need to exchange a "smaller number" on the left with a "larger number" on the right to make the current arrangement larger and get the next arrangement.
• • At the same time, keep the "smaller number" to the right and the "larger number" as small as possible. When the exchange is completed, the numbers to the right of the "larger number" need to be rearranged in ascending order. In this way, the amplitude of enlargement can be reduced as much as possible while ensuring that the new arrangement is larger than the original arrangement.
• Take the arrangement [4,5,2,6,3,1] as an example:
• • The combination of a pair of qualified "smaller number" and "larger number" that can be found is 2 and 3. The "smaller number" should be as right as possible and the "larger number" should be as small as possible.
• • When the exchange is completed, the arrangement changes to [4,5,3,6,2,1]. At this time, you can rearrange the sequence to the right of the "smaller fraction", and the sequence changes to [4,5,3,1,2,6].
• Specifically, the algorithm is described in this way. For the arrangement a with length n:
• • First, find the first sequence pair (i,i+1) from back to front, satisfying a[i] < a[i + 1]. In this way, the "smaller fraction" is a[i]. At this time [i+1,n) must be a descending sequence.
• • If the sequence pair is found, the first element j is found from back to front in the interval [i+1,n) to satisfy a [i] < a[j]. In this way, the "larger number" is a[j].
• • Exchange a[i] and a[j]. At this time, it can be proved that the interval [i+1,n) must be in descending order. You can directly use the double pointer to reverse the interval [i+1,n) to make it into ascending order without sorting the interval.

• C + + example:

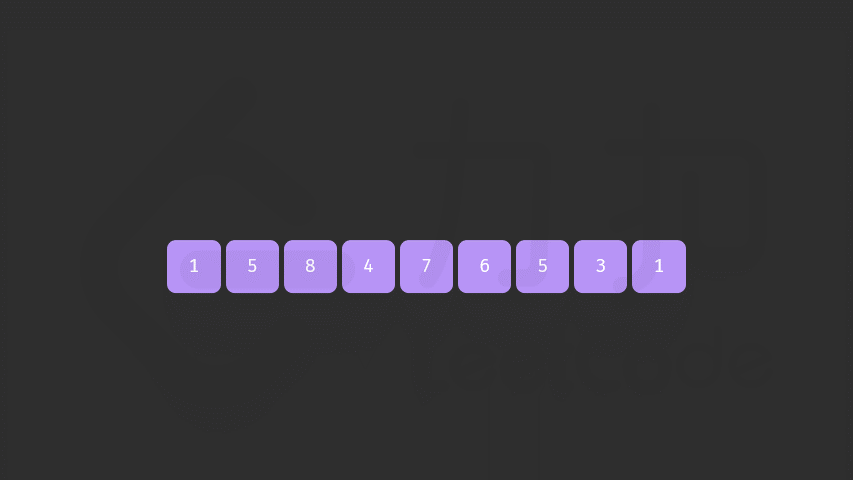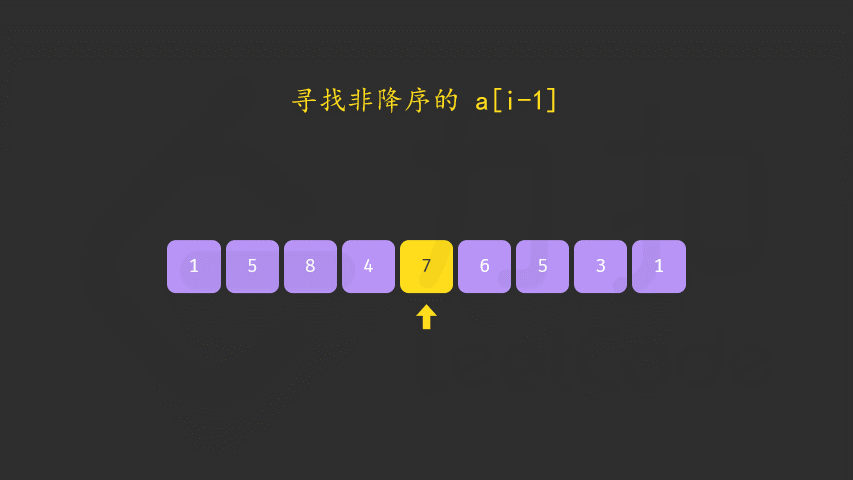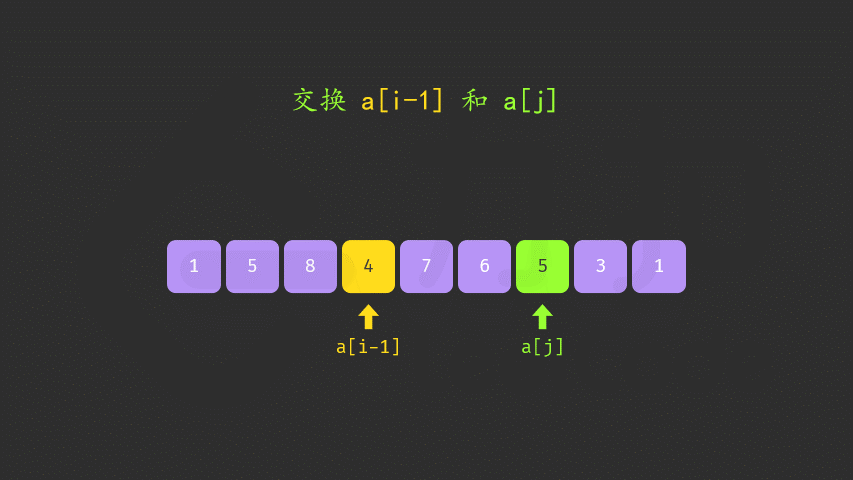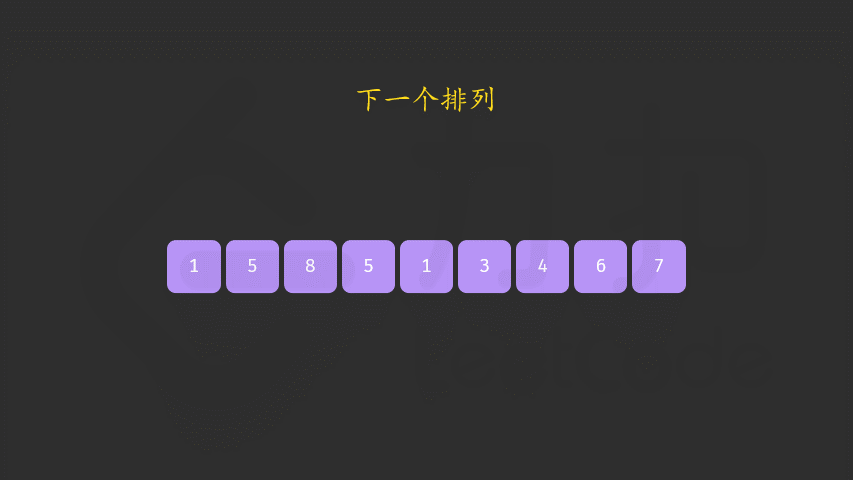
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int i = nums.size() - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.size() - 1;
            while (j >= 0 && nums[i] >= nums[j]) {
                j--;
            }
            swap(nums[i], nums[j]);
        }
        reverse(nums.begin() + i + 1, nums.end());
    }
};

• Java example:

class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[i] >= nums[j]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i + 1);
    }

    public void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public void reverse(int[] nums, int start) {
        int left = start, right = nums.length - 1;
        while (left < right) {
            swap(nums, left, right);
            left++;
            right--;
        }
    }
}

② Standard "next permutation" algorithm

• The standard "next permutation" algorithm can be described as:
• • Find the first adjacent element pair (i,j) in ascending order from back to front, which satisfies a [i] < a [J], and [j,end) must be in descending order at this time;
• • Find the first k satisfying A[i] < A[k] in [J, end]. A[i] and A[k] are respectively the "decimal" and "large" mentioned above;
• • Exchange A[i] with A[k];
• • It can be concluded that [j,end) must be in descending order and [J, end] must be reversed to make it in ascending order;
• • If no matching adjacent element pair is found in the first step of step, it indicates that the current [begin,end) is in a descending order, then skip to step 4 directly.
• Take the next arrangement of 12385764 as an example:

• First, find the first adjacent ascending element pair (i,j) from back to front, where i=4, j=5, and the corresponding value is 5, 7:

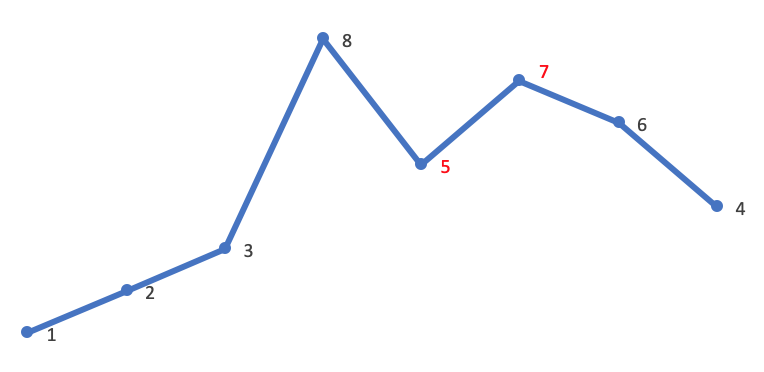
• Then look for the first value A[k] greater than A[i] in [J, end], where A[i] is 5, so A[k] is 6:

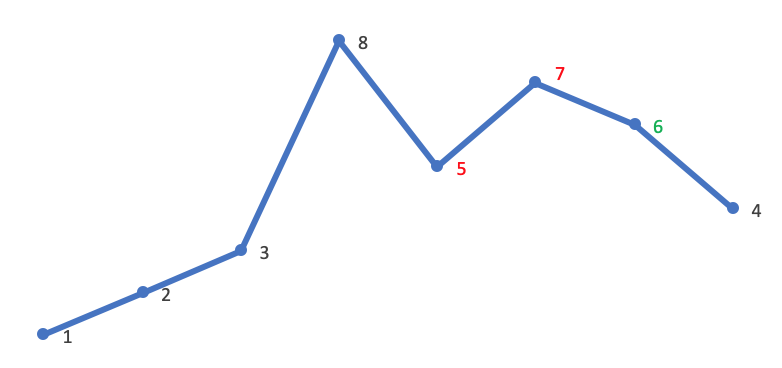
• Exchange A[i] and A[k], here exchange 5 and 6:

• At this time [j,end) must be in descending order, inverse [J, end], so that it is in ascending order. Here, inverse [7,5,4]:

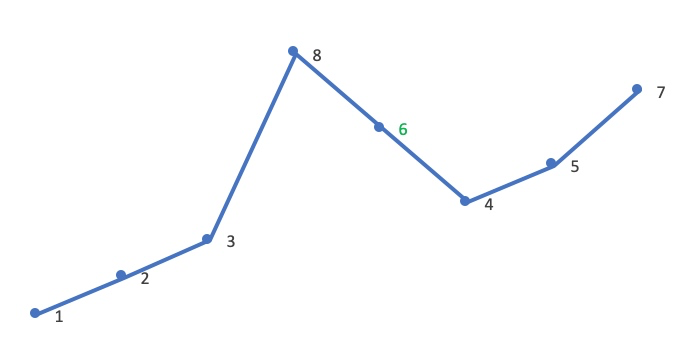
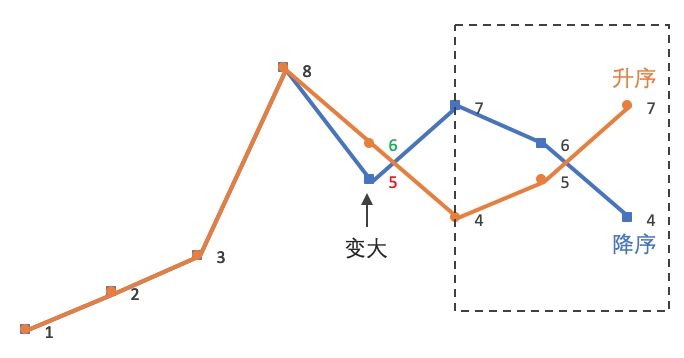
• Therefore, the next arrangement of 12385764 is 12386457. Finally, compare the two adjacent permutations (orange is the next permutation in blue):

• Example:

class Solution {
    public void nextPermutation(int[] nums) {
        int len = nums.length;
        for (int i = len - 1; i > 0; i--) {
                if (nums[i] > nums[i - 1]) {
                    Arrays.sort(nums, i, len);
                    for (int j = i; j <len; j++) {
                        if (nums[j] > nums[i - 1]) {
                            int temp = nums[j];
                            nums[j] = nums[i - 1];
                            nums[i - 1] = temp;
                            return;
                        }
                    }
                }
            }
    	Arrays.sort(nums);
		return;  
    }
 }

func nextPermutation(nums []int) {
	if len(nums) <= 1 {
		return
	}

	i, j, k := len(nums)-2, len(nums)-1, len(nums)-1

	// find: A[i]<A[j]
	for i >= 0 && nums[i] >= nums[j] {
		i--
		j--
	}

	if i >= 0 { // Not the last permutation
		// find: A[i]<A[k]
		for nums[i] >= nums[k] {
			k--
		}
		// swap A[i], A[k]
		nums[i], nums[k] = nums[k], nums[i]
	}

	// reverse A[j:end]
	for i, j := j, len(nums)-1; i < j; i, j = i+1, j-1 {
		nums[i], nums[j] = nums[j], nums[i]
	}
}