Learning objectives:
The eight queens chessboard problem is solved by Python language and backtracking method, and the visual output is realized
Learning content:
problem analysis
Problem Description: the eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The question was put forward by international chess player Max Bethel in 1848: in August × Eight queens are placed on the 8-grid chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash. Ask how many kinds of pendulum methods there are. Gauss believes there are 76 options. In 1854, different authors published 40 different solutions in the chess magazine in Berlin. Later, 92 results were solved by the method of graph theory.
Curriculum requirements
Requirements: use the backtracking method to solve the eight queens problem, output all the solutions of the problem, and realize the visual display.
The above are the requirements of this course design.
Algorithm ideas and Solutions
Characteristics of backtracking method
Backtracking method is an optimization search method, which searches in depth first according to the optimization conditions to achieve the goal. When a certain step is searched and it is found that the original selection is not optimal or fails to achieve the goal, it will go back to one step and reselect. This technology of going back and going again if it fails is called backtracking method, and a state that meets the backtracking conditions is called "backtracking point".
The backtracking method starts from the initial state, searches the solution of the problem according to the depth first search method and the condition constraints of generating sub nodes. When it is found that the current node does not meet the solution conditions, it will backtrack and try other paths. Backtracking method is a search method of "entering if you can, changing if you can't, and returning if you can't".
Key technology of algorithm
(1) Define the solution space of the problem
The solution of the n-queen problem is in the form of N tuple: {x1, x2,..., xi,..., xn}. The component xi indicates that the ith queen is placed in the ith row and the xi column. The value of xi is 1, 2,..., n. For example, x2=5 indicates that the second queen is placed in Row 2 and column 5. Explicit constraints for different rows.
(2) Organizational structure of solution space
The solution space of the n-queen problem is an m (m=n) fork tree, and the depth of the tree is n, as shown in the figure.

(3) Search solution space
·Constraints
When placing the t-th queen in row T, the position of the t-th queen cannot be in the same column and slash as the first t-1 queen. Queen I and queen j have different columns, i.e. xi=xj, and different slashes | I-j |= [xi-xj].
·Gauge condition
This problem does not exist whether the placement scheme is good or bad, so there is no need to set clearance conditions.
·Search process
Start from the root and search in the way of depth first search. The root node is a live node and is the current extension node. In the search process, the current extended node moves to a new node along the depth direction to judge whether the new node meets the implicit constraint. If satisfied, the new node becomes the live node and the current extended node, and continues the deep search; If not, switch to the sibling node of the new node to continue the search; If the new node has no sibling nodes, or all of its sibling nodes have been searched, the extended node becomes a dead node, and the search continues back to its parent node. The search process until the root node of the problem is found and becomes a dead node.
Algorithm optimization
1. Algorithm complexity analysis
(1) Time complexity
The solution space of n-queen problem is an m (m=n) fork tree, and the depth of the tree is n. In the worst case, in addition to the last layer, there are 1+n+n2 +... + n(n-1)=(nn-1)(n-1) ≈ n(n-1) nodes in the solution space tree that need to be expanded, and each of these nodes needs to expand n branches, the total number of branches is n, and each branch needs O(n) time to judge the constraint function and the constraint conditions, so it takes O(n(n-1)). It takes O(n) to output the current optimal solution at the leaf node. In the worst case, it takes O(n(n-1)) to search back to each leaf node, and the number of leaves is NN. Therefore, the time complexity is O(n(n-1)).
(2) Spatial complexity
Another important feature of backtracking method is to generate solution space while searching. At any time in the search process, only the path from the start node to the current extension node is reserved, and the longest path from the start node is n. In the program, we use the x [] array to record the longest path as the feasible solution, so the spatial complexity of the algorithm is O(n).
2. Algorithm optimization and expansion
In the above solution process, our solution space is too large, so the time complexity is very high, and the efficiency of the algorithm will certainly be reduced. The smaller the solution space, the higher the efficiency of the algorithm. Because the solution space is the scope we need to search for solutions. It's like looking for a needle in a haystack. It's very difficult. It's less difficult to look for a needle in a basin. It's easier to look for a needle in a bowl.
Let's simplify it with the four queens problem
For the four queen problem, the explicit constraint is the solution space tree of different rows, as shown in the figure

Explicit constraints can control the size of solution space, while implicit constraints determine the feasible or optimal solution in the process of searching solution space.
For example, for a branch with x1=1, x2 cannot be equal to 1, because it is the same column. If x1=1 and x2=2, x3 can no longer be equal to 1 and 2, that is, the value of xt cannot be the same as that of the previous t-1 solution. The number of children generated by each layer node is one less than that of the previous layer. For the four queens problem, the explicit constraints are the solution space trees of different rows and columns, as shown in the figure.
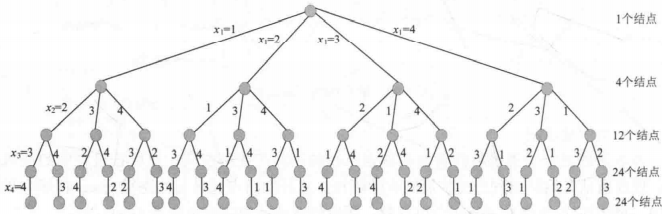
We can clearly see that the solution space becomes much smaller, which greatly reduces the time complexity of the algorithm. At this time, the time complexity is O(n3).
Python code implementation
Here's a reference https://blog.csdn.net/weixin_44227192/article/details/106931823?utm_medium=distribute.pc_relevant.none -task-blog-baidujs_ Title-0 & SPM = 1001.2101.3001.4242 code of the boss, and some modifications have been made
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
# ------------------------
#Set Chinese character set to solve the problem of Chinese garbled code in drawing
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
#Placement function
def Queen_set(n):
global num
queen_list2=[i+1 for i in queen_list]
if n==8:
print("The first"+str(num)+"species:",(1,queen_list2[0]),(2,queen_list2[1]),(3,queen_list2[2]),(4,queen_list2[3])
,(5,queen_list2[4]),(6,queen_list2[5]),(7,queen_list2[6]),(8,queen_list2[7]))
plot_chess(queen_list)
num+=1
return
else:
for i in range(8):
if check(n,i):
queen_list.append(i) #Place queen in current position
Queen_set(n+1) #Recursion, enter the next level of search
queen_list.pop() #Backtrack the key points and clear the wrong data in the previous step
#Check whether the current position meets the requirements
#Depth: search depth index: current placement
def check(depth,index):
if depth==0:
return True
else:
for i in range(depth):
if queen_list[i] == index: #Determine whether the column conforms to
return False
#Judge whether the diagonal rule is met
elif index==queen_list[i]-depth+i or index==queen_list[i]+depth-i:
return False
return True
#Draw the chessboard and save the solution results
def plot_chess(result):
global num
mat=np.zeros((8,8))
for i in range(8):
for j in range(8):
if result[i]==j:
mat[i,j]=1
elif (i+j)%2==0:
mat[i,j]=-1
else:
mat[i,j]=0
my_cmap=matplotlib.colors.LinearSegmentedColormap.from_list('my_camp',['white','black','red'],3)
plt.imshow(mat,cmap=my_cmap)
plt.title("The first"+str(num)+"A solution",fontsize=16)
plt.xticks([])
plt.yticks([])
plt.savefig('C:/Users/zhous/Desktop/Algorithm Course Design/EightQueens Palace/'+str(num)+'.png') #Save the path of the picture and modify it yourself
queen_list = []
num = 1
Queen_set(0)
Result visualization
Here's a reference https://blog.csdn.net/weixin_45405128/article/details/102510877?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162427419916780261924951%2522%252C%2522scm%2522%253A%252220140713.130102334 …%2522%257D&request_ id=162427419916780261924951&biz_ id=0&utm_ medium=distribute. pc_ search_ result. none-task-blog-2allbaidu_ landing_ v2~default-1-102510877. first_ rank_ v2_ pc_ rank_ v29&utm_ Term =% E7% 94% a8matplotlib% E7% 94% BB% E6% A3% 8b% E7% 9b% 98 & SPM = 1018.2226.3001.4187 boss's visual chessboard code
#Draw the chessboard and save the solution results
def plot_chess(result):
global num
mat=np.zeros((8,8))
for i in range(8):
for j in range(8):
if result[i]==j:
mat[i,j]=1
elif (i+j)%2==0:
mat[i,j]=-1
else:
mat[i,j]=0
my_cmap=matplotlib.colors.LinearSegmentedColormap.from_list('my_camp',['white','black','red'],3)
plt.imshow(mat,cmap=my_cmap)
plt.title("The first"+str(num)+"A solution",fontsize=16)
plt.xticks([])
plt.yticks([])
plt.savefig('C:/Users/zhous/Desktop/Algorithm Course Design/EightQueens Palace/'+str(num)+'.png') #Save the path of the picture and modify it yourself
Learning gains:
solve the problem
1, Operation error caused by font problem
When setting the Chinese character set to solve the problem of Chinese garbled code in drawing, we encountered an error in operation.

As shown in the figure, the displayed error message means that the corresponding font is not found. To solve this problem, we searched CSDN. The specific steps are as follows:
- Locate the Mircosoft YaHei UI font file
Generally, you can see it in C:\Windows\Fonts, as shown below

- Copy the font file to the folder below. In your own python installation directory F: \ python 3 7\Lib\site-packages\matplotlib\mpl-data\fonts\ttf
After the copy is completed, there will be msyh in this folder TTC file
- Modify the matplotlibrc file
Open the matplotlibrc file
(1) Delete font The # in front of the family and change the colon to "Microsoft YaHei";
(2) Delete font Before sans serif # and add "Microsoft YaHei" after colon


After the modification is completed, save it, close python, restart the running program, and solve it successfully.
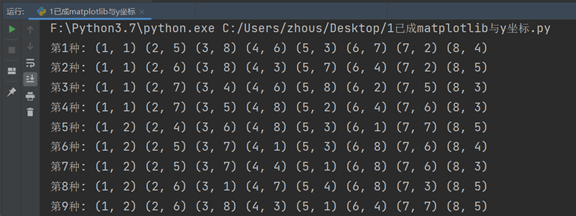
2, The output result format is not clear
In the running result, each number in the output list represents the vertical coordinates, i.e. column coordinates, and the horizontal coordinates are from 1 to 8 by default, as shown in the figure:

We will the original code
print("The first"+str(num)+"species:",queen_list2)
Change to
print("The first"+str(num)+"species:",(1,queen_list2[0]),(2,queen_list2[1]),(3,queen_list2[2]),(4,queen_list2[3]),(5,queen_list2[4]),(6,queen_list2[5]),(7,queen_list2[6]),(8,queen_list2[7]))
After that, we successfully output the coordinate values in (x, y) format
Learning gains:
Through this course design, we have well solved the placement problem of the eight queens, enriched our programming language knowledge and accumulated experience in solving problems.
Learning output:
1. Technical notes 3 times
2. CSDN technology blog 1
3. 1 course design report
4. 1 case of PPT demonstration