in the course of stellar structure and evolution, mesa was used to simulate stellar evolution. At that time, when drawing the evolution animation of various stars, I thought that if the effective temperature of stars could be mapped to the specific corresponding color, would the animation be more vivid? So I went to the Internet to collect the relationship between blackbody temperature and color, but I didn't find anything. With ddl coming soon, I had to give up.
coincidentally, before long, another old colleague asked me A similar question: why is the temperature difference between type A stars and electric welding so large that the light emitted is blue and white? At that time, my answer was that the former can be regarded as blackbody, while the latter is not. Their spectra are different, and the results of integral operation that can be transformed into color are different, resulting in different colors.
so the question is, how does the spectrum calculate the corresponding color? Therefore, I collected part of the literature and web materials of chromatics, and finally found the following answers.
Spectrum to color calculation process
the calculation process from spectrum to color is roughly as follows:
spectrum & CMF of CIE XYZ trichromatic system → \rightarrow → XYZ component → \rightarrow → RGB component → \rightarrow → normalized RGB color that can be used directly
spectrum
it is known in optics that the radiation intensity of an object in various bands can be measured by spectrum
ϕ
λ
(
λ
)
\phi_\lambda(\lambda)
ϕλ ( λ) To describe, where
λ
\lambda
λ Is the wavelength. With spectrum
ϕ
λ
(
λ
)
\phi_\lambda(\lambda)
ϕλ ( λ) After that, each specified wavelength range can be obtained by integration
[
λ
1
,
λ
2
]
[\lambda_1,\ \lambda_2]
[ λ 1, λ Radiation intensity in [2]:
I
12
=
∫
λ
1
λ
2
ϕ
λ
(
λ
)
d
λ
I_{12}=\int_{\lambda_1}^{\lambda_2}\phi_\lambda(\lambda)d\lambda
I12=∫λ1λ2ϕλ(λ)dλ
for blackbody, the radiation is:
S
λ
(
λ
,
T
)
=
8
π
h
c
λ
5
1
e
h
c
/
λ
k
T
−
1
S_\lambda(\lambda,\ T)=\frac{8\pi hc}{\lambda^5}\frac{1}{e^{hc/\lambda kT}-1}
Sλ(λ, T)=λ58πhcehc/λkT−11
Quantitative description of color -- CIE XYZ trichromatic system
when it comes to the quantitative description of color, the most famous color coordinate system is the CIE XYZ Trichromatic System, which defines the three basis vectors in the color space as X, Y and Z respectively. All colors in this system are described by the linear superposition of these three basis vectors. In other words, as long as you know the values of X, Y and Z, you can determine a specific color
but how do you determine x, Y and Z? At this time, it is necessary to use the "human eye transmittance curve" similar to the transmittance curve of the filter, which is called color matching functions (CMF) in chromatics. CMF decomposes the photosensitive characteristics of human eyes into three components: X, Y and Z, so as to obtain three "transmittance curves" respectively x ˉ ( λ ) \bar x(\lambda) xˉ(λ), y ˉ ( λ ) \bar y(\lambda) y ˉ ( λ) and z ˉ ( λ ) \bar z(\lambda) zˉ(λ):
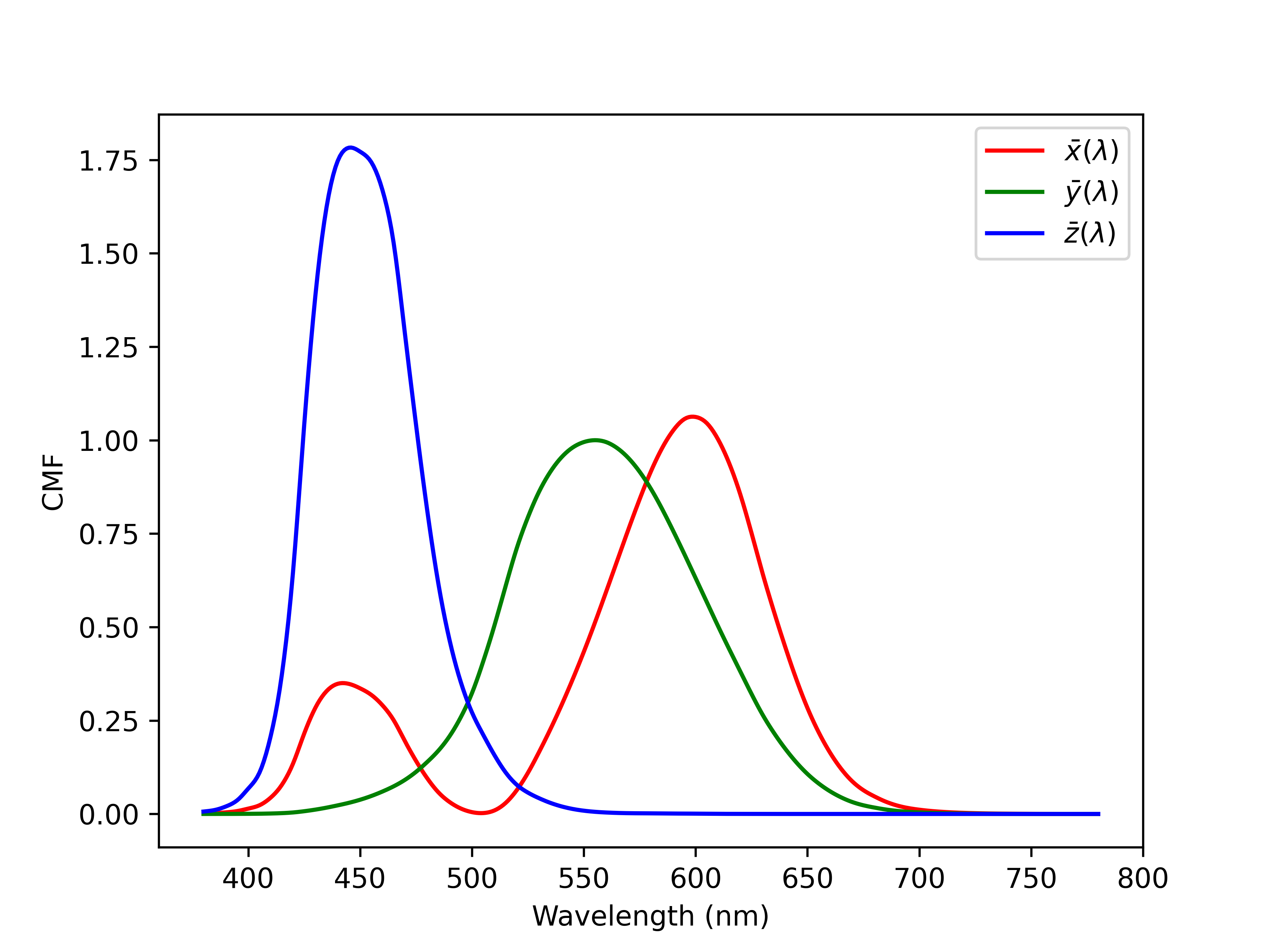
similar to the flow calculation in astronomical observation, for any spectrum
ϕ
λ
(
λ
)
\phi_\lambda(\lambda)
ϕλ ( λ), The three components as like as two peas are similar in terms of flow.
X
=
k
∫
380
n
m
780
n
m
ϕ
λ
(
λ
)
x
ˉ
(
λ
)
d
λ
Y
=
k
∫
380
n
m
780
n
m
ϕ
λ
(
λ
)
y
ˉ
(
λ
)
d
λ
Z
=
k
∫
380
n
m
780
n
m
ϕ
λ
(
λ
)
z
ˉ
(
λ
)
d
λ
\begin{aligned} X&=k\int_{380\ \mathrm{nm}}^{780\ \mathrm{nm}}\phi_\lambda(\lambda)\bar x(\lambda)d\lambda\\ Y&=k\int_{380\ \mathrm{nm}}^{780\ \mathrm{nm}}\phi_\lambda(\lambda)\bar y(\lambda)d\lambda\\ Z&=k\int_{380\ \mathrm{nm}}^{780\ \mathrm{nm}}\phi_\lambda(\lambda)\bar z(\lambda)d\lambda \end{aligned}
XYZ=k∫380 nm780 nmϕλ(λ)xˉ(λ)dλ=k∫380 nm780 nmϕλ(λ)yˉ(λ)dλ=k∫380 nm780 nmϕλ(λ)zˉ(λ)dλ
after calculating X, Y and Z, normalize them:
x
=
X
X
+
Y
+
Z
y
=
Y
X
+
Y
+
Z
z
=
Z
X
+
Y
+
Z
\begin{aligned} x&=\frac{X}{X+Y+Z}\\ y&=\frac{Y}{X+Y+Z}\\ z&=\frac{Z}{X+Y+Z} \end{aligned}
xyz=X+Y+ZX=X+Y+ZY=X+Y+ZZ
(
x
,
y
,
z
)
(x,\ y,\ z)
(x, y, z) degree of freedom is 2, omitted
z
z
z coordinate, drawn
(
x
,
y
)
(x,\ y)
The (x, y) plane is
(
x
,
y
)
(x,\ y)
(x, y) chromaticity diagram. So far, any color can be quantitatively represented by the coordinates on this plane
XYZ to RGB conversion
in fact, when the earliest CIE 1931 specification was proposed, the RGB system we are familiar with appeared earlier than the XYZ system. Because they all use three different basis vectors in the color space, the corresponding linear transformation can be carried out between the two systems
the parameters of linear transformation can also be found in many literatures. For example, RGB is transformed to XYZ as follows:
(
X
Y
Z
)
=
(
2.768892
1.751748
1.130160
1.000000
4.590700
0.060100
0
0.056508
5.594292
)
(
R
G
B
)
\left(\begin{matrix} X\\Y\\Z \end{matrix}\right)= \left(\begin{matrix} 2.768892 & 1.751748 & 1.130160\\ 1.000000 & 4.590700 & 0.060100\\ 0 & 0.056508 & 5.594292 \end{matrix}\right) \left(\begin{matrix} R\\G\\B \end{matrix}\right)
⎝⎛XYZ⎠⎞=⎝⎛2.7688921.00000001.7517484.5907000.0565081.1301600.0601005.594292⎠⎞⎝⎛RGB⎠⎞
the inverse of the transformation matrix can be used for the transformation from XYZ to RGB. After the transformation, the corresponding normalization can be carried out according to the demand, and the color can be displayed on the display equipment adopting RGB specification
Display of algorithm operation results
Blackbody color at different temperatures
according to the blackbody spectrum and CMF mentioned above, calculate the blackbody at different temperatures to obtain XYZ, and then obtain RGB through linear transformation and normalization, and draw the following results:

there is still a large deviation between this figure and various color temperature reference figures, which may be due to the different use of CMF curve (the CMF curve here is pulled out from the corresponding database in python's color science package)
Herot improvement
now that we know the specific correspondence between blackbody temperature and color, we have tried to improve a herogram drawn a few months ago. Now the color of each point can correspond to the effective (blackbody) temperature, which is more scientific:
 | 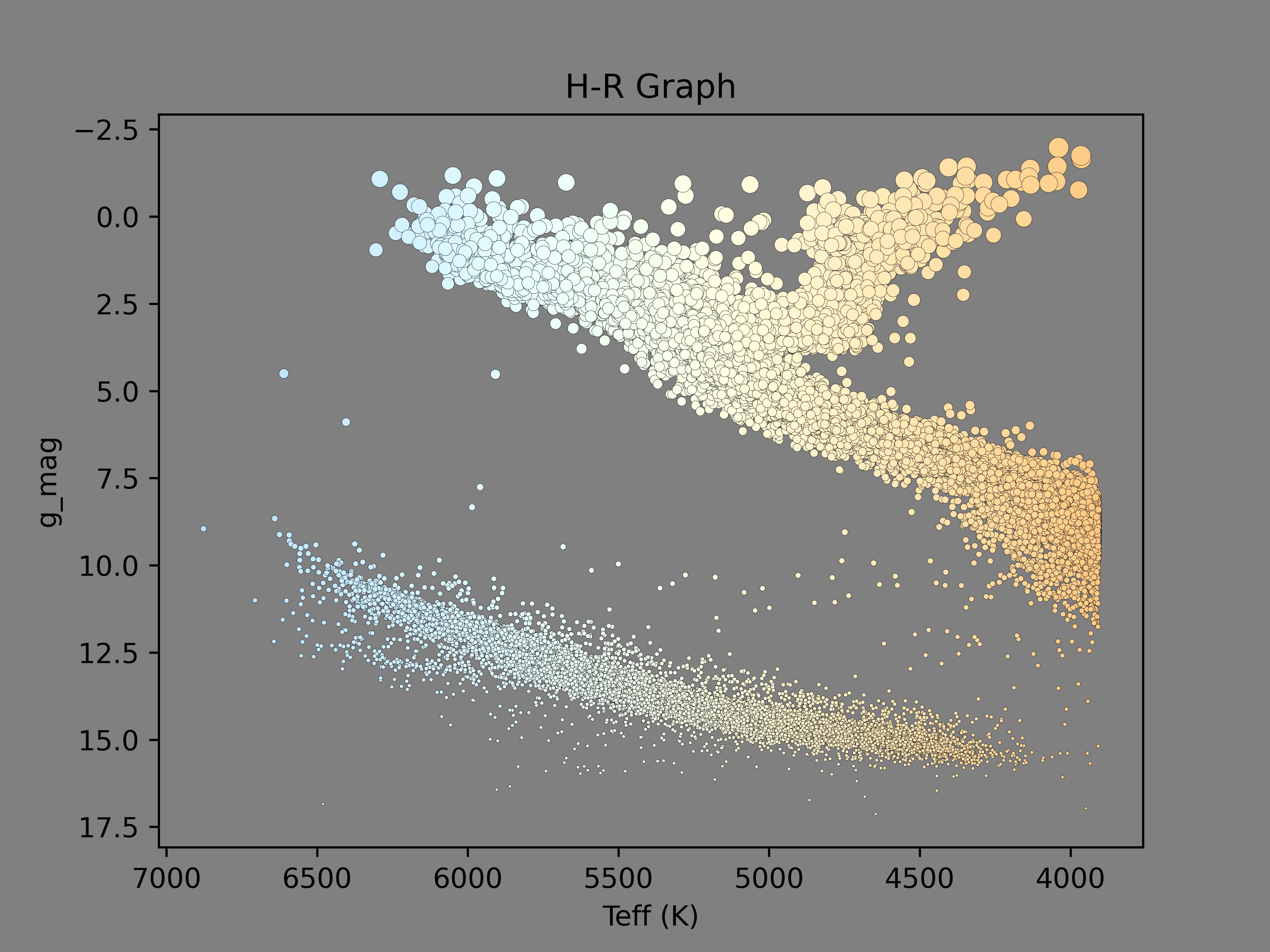 |
|---|
The first question: Why are the radiation colors the same at different temperatures?
the answer is naturally caused by different spectra. With different spectra, the X, Y and Z components obtained are different, and the colors will naturally be different
there are also documents (mccamy, C., 1992) that study the isotherms in CIE - they are straight lines that approximately radiate different slopes outward with a certain point as the center. On the same straight line, the corresponding temperature of the object is equal. In other words, objects with the same temperature do show different colors with different spectra
reference
[1] JÁNOS SCHANDA (2007). UNDERSTANDING THE CIE SYSTEM, 29-34.
[2] McCamy, C. (1992). Correlated color temperature as an explicit function of chromaticity coordinates . Color Research & Application, 17(2), 142–144.
Related code
Conversion between blackbody spectrum and RGB color
import numpy as np
import matplotlib.pyplot as plt
import json
from colour.plotting import plot_chromaticity_diagram_CIE1931
def load_cmf():
"""
obtain XYZ Coordinate system cmf
Returns
-------
[xbar, ybar, zbar] : [float[], float[], float[]]
Of three coordinate variables cmf
"""
xbar = []
ybar = []
zbar = []
with open("data_cmfs_standard_observer.json", "r") as f:
D = json.load(f)
for each_waveLength in range(380, 781):
each_waveLength_str = str(each_waveLength)
[each_xbar, each_ybar, each_zbar] = D[each_waveLength_str]
xbar.append(each_xbar)
ybar.append(each_ybar)
zbar.append(each_zbar)
return [xbar, ybar, zbar]
def get_bb_spectrum(T):
"""
Calculate the corresponding blackbody spectrum at a certain temperature
Parameters
----------
T : float
temperature(K)
Returns
-------
waveLength : float[]
wavelength(nm)
bb_spectrum : float[]
Calculated normalized blackbody spectrum
"""
h = 6.626e-34
c = 3e8
k = 1.381e-23
waveLength = np.arange(380, 781, 1) # unit : nm
waveLength_metric = waveLength / 1e9 # unit : m
bb_spectrum = 8 * np.pi * h * c / waveLength_metric**5 / (np.exp(h * c / (waveLength_metric * k * T)) - 1)
bb_spectrum = bb_spectrum / max(bb_spectrum) # normalization
return [waveLength, bb_spectrum]
def plotCMF(waveLength, xbar, ybar, zbar):
"""
draw CMF
"""
plt.plot(waveLength, xbar, 'r-', label=r'$\bar x(\lambda)$')
plt.plot(waveLength, ybar, 'g-', label=r'$\bar y(\lambda)$')
plt.plot(waveLength, zbar, 'b-', label=r'$\bar z(\lambda)$')
plt.xlabel('Wavelength (nm)')
plt.ylabel('CMF')
plt.legend()
plt.savefig("CMF.png", dpi=600)
def convolution(fx1, fx2):
"""
Calculate the integral of the multiplication of two functions, which has been satisfied x Conditions corresponding to axis coordinates
"""
fx1 = np.array(fx1)
fx2 = np.array(fx2)
F = np.sum(fx1 * fx2)
return F
def calculate_CIE_pos(bb_spectrum, xbar, ybar, zbar):
"""
According to the blackbody spectrum and CMF,calculation CIE coordinate
"""
X = convolution(bb_spectrum, xbar)
Y = convolution(bb_spectrum, ybar)
Z = convolution(bb_spectrum, zbar)
x = X / (X + Y + Z)
y = Y / (X + Y + Z)
z = Z / (X + Y + Z)
return [x, y, z]
def show_bb_color_in_CIE(T):
"""
stay CIE The temperature displayed on the is T Corresponding color of bold
"""
[xbar, ybar, zbar] = load_cmf()
plot_chromaticity_diagram_CIE1931(standalone=False)
[waveLength, bb_spectrum] = get_bb_spectrum(T=T)
[x, y, z] = calculate_CIE_pos(bb_spectrum, xbar, ybar, zbar)
plt.plot(x, y, 'k.')
plt.show()
def from_xyz_to_RGB(x, y, z):
"""
take CIE Convert coordinates on to RGB coordinate
"""
M = np.matrix([[0.41845516, -0.15865714, -0.08283193],
[-0.09116486, 0.25242564, 0.01570531],
[0.00092086, -0.00254975, 0.17859499]])
xyz = np.matrix([[x], [y], [z]])
RGB = M * xyz
RGB = RGB / max(RGB)
RGB[np.where(RGB < 0)] = 0
RGB = np.array(RGB)
return [RGB[0][0], RGB[1][0], RGB[2][0]]
def plot_bb_color_temperature_relation():
"""
Draw the color in bold-Temperature diagram
"""
[xbar, ybar, zbar] = load_cmf()
deltaT = 50
plt.figure(figsize=(10,1))
for T in range(1000, 12000, deltaT):
[waveLength, bb_spectrum] = get_bb_spectrum(T=T)
[x, y, z] = calculate_CIE_pos(bb_spectrum, xbar, ybar, zbar)
RGB = from_xyz_to_RGB(x, y, z)
plt.fill([T, T+deltaT, T+deltaT, T, T], [0, 0, 1, 1, 0], c=RGB)
plt.yticks([])
plt.xlabel("Blackbody Temperature (K)")
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.tight_layout()
plt.savefig("bb_color_temperature_relation.png", dpi=600)
def bb_temperature_to_RGB(T):
"""
Convert the color corresponding to the temperature of the blackbody into RGB value
Returns
-------
RGB : float[3]
RGB Value, which has been normalized and can be used directly in pyplot Used in
"""
[xbar, ybar, zbar] = load_cmf()
[waveLength, bb_spectrum] = get_bb_spectrum(T=T)
[x, y, z] = calculate_CIE_pos(bb_spectrum, xbar, ybar, zbar)
RGB = from_xyz_to_RGB(x, y, z)
return RGB
if __name__ == "__main__":
RGB = bb_temperature_to_RGB(T=5000)
print(RGB)
CMF under CIE 1931 specification (extracted from colour science package and can be copied directly)
json format, key is the wavelength, the unit is nanometer, and value is x ˉ ( λ ) \bar x(\lambda) xˉ(λ), y ˉ ( λ ) \bar y(\lambda) y ˉ ( λ) and z ˉ ( λ ) \bar z(\lambda) z ˉ ( λ) Value of
{"360": [0.0001299, 3.917e-06, 0.0006061], "361": [0.000145847, 4.393581e-06, 0.0006808792], "362": [0.0001638021, 4.929604e-06, 0.0007651456], "363": [0.0001840037, 5.532136e-06, 0.0008600124], "364": [0.0002066902, 6.208245e-06, 0.0009665928], "365": [0.0002321, 6.965e-06, 0.001086], "366": [0.000260728, 7.813219e-06, 0.001220586], "367": [0.000293075, 8.767336e-06, 0.001372729], "368": [0.000329388, 9.839844e-06, 0.001543579], "369": [0.000369914, 1.104323e-05, 0.001734286], "370": [0.0004149, 1.239e-05, 0.001946], "371": [0.0004641587, 1.388641e-05, 0.002177777], "372": [0.000518986, 1.555728e-05, 0.002435809], "373": [0.000581854, 1.744296e-05, 0.002731953], "374": [0.0006552347, 1.958375e-05, 0.003078064], "375": [0.0007416, 2.202e-05, 0.003486], "376": [0.0008450296, 2.483965e-05, 0.003975227], "377": [0.0009645268, 2.804126e-05, 0.00454088], "378": [0.001094949, 3.153104e-05, 0.00515832], "379": [0.001231154, 3.521521e-05, 0.005802907], "380": [0.001368, 3.9e-05, 0.006450001], "381": [0.00150205, 4.28264e-05, 0.007083216], "382": [0.001642328, 4.69146e-05, 0.007745488], "383": [0.001802382, 5.15896e-05, 0.008501152], "384": [0.001995757, 5.71764e-05, 0.009414544], "385": [0.002236, 6.4e-05, 0.01054999], "386": [0.002535385, 7.234421e-05, 0.0119658], "387": [0.002892603, 8.221224e-05, 0.01365587], "388": [0.003300829, 9.350816e-05, 0.01558805], "389": [0.003753236, 0.0001061361, 0.01773015], "390": [0.004243, 0.00012, 0.02005001], "391": [0.004762389, 0.000134984, 0.02251136], "392": [0.005330048, 0.000151492, 0.02520288], "393": [0.005978712, 0.000170208, 0.02827972], "394": [0.006741117, 0.000191816, 0.03189704], "395": [0.00765, 0.000217, 0.03621], "396": [0.008751373, 0.0002469067, 0.04143771], "397": [0.01002888, 0.00028124, 0.04750372], "398": [0.0114217, 0.00031852, 0.05411988], "399": [0.01286901, 0.0003572667, 0.06099803], "400": [0.01431, 0.000396, 0.06785001], "401": [0.01570443, 0.0004337147, 0.07448632], "402": [0.01714744, 0.000473024, 0.08136156], "403": [0.01878122, 0.000517876, 0.08915364], "404": [0.02074801, 0.0005722187, 0.09854048], "405": [0.02319, 0.00064, 0.1102], "406": [0.02620736, 0.00072456, 0.1246133], "407": [0.02978248, 0.0008255, 0.1417017], "408": [0.03388092, 0.00094116, 0.1613035], "409": [0.03846824, 0.00106988, 0.1832568], "410": [0.04351, 0.00121, 0.2074], "411": [0.0489956, 0.001362091, 0.2336921], "412": [0.0550226, 0.001530752, 0.2626114], "413": [0.0617188, 0.001720368, 0.2947746], "414": [0.069212, 0.001935323, 0.3307985], "415": [0.07763, 0.00218, 0.3713], "416": [0.08695811, 0.0024548, 0.4162091], "417": [0.09717672, 0.002764, 0.4654642], "418": [0.1084063, 0.0031178, 0.5196948], "419": [0.1207672, 0.0035264, 0.5795303], "420": [0.13438, 0.004, 0.6456], "421": [0.1493582, 0.00454624, 0.7184838], "422": [0.1653957, 0.00515932, 0.7967133], "423": [0.1819831, 0.00582928, 0.8778459], "424": [0.198611, 0.00654616, 0.959439], "425": [0.21477, 0.0073, 1.0390501], "426": [0.2301868, 0.008086507, 1.1153673], "427": [0.2448797, 0.00890872, 1.1884971], "428": [0.2587773, 0.00976768, 1.2581233], "429": [0.2718079, 0.01066443, 1.3239296], "430": [0.2839, 0.0116, 1.3856], "431": [0.2949438, 0.01257317, 1.4426352], "432": [0.3048965, 0.01358272, 1.4948035], "433": [0.3137873, 0.01462968, 1.5421903], "434": [0.3216454, 0.01571509, 1.5848807], "435": [0.3285, 0.01684, 1.62296], "436": [0.3343513, 0.01800736, 1.6564048], "437": [0.3392101, 0.01921448, 1.6852959], "438": [0.3431213, 0.02045392, 1.7098745], "439": [0.3461296, 0.02171824, 1.7303821], "440": [0.34828, 0.023, 1.74706], "441": [0.3495999, 0.02429461, 1.7600446], "442": [0.3501474, 0.02561024, 1.7696233], "443": [0.350013, 0.02695857, 1.7762637], "444": [0.349287, 0.02835125, 1.7804334], "445": [0.34806, 0.0298, 1.7826], "446": [0.3463733, 0.03131083, 1.7829682], "447": [0.3442624, 0.03288368, 1.7816998], "448": [0.3418088, 0.03452112, 1.7791982], "449": [0.3390941, 0.03622571, 1.7758671], "450": [0.3362, 0.038, 1.77211], "451": [0.3331977, 0.03984667, 1.7682589], "452": [0.3300411, 0.041768, 1.764039], "453": [0.3266357, 0.043766, 1.7589438], "454": [0.3228868, 0.04584267, 1.7524663], "455": [0.3187, 0.048, 1.7441], "456": [0.3140251, 0.05024368, 1.7335595], "457": [0.308884, 0.05257304, 1.7208581], "458": [0.3032904, 0.05498056, 1.7059369], "459": [0.2972579, 0.05745872, 1.6887372], "460": [0.2908, 0.06, 1.6692], "461": [0.2839701, 0.06260197, 1.6475287], "462": [0.2767214, 0.06527752, 1.6234127], "463": [0.2689178, 0.06804208, 1.5960223], "464": [0.2604227, 0.07091109, 1.564528], "465": [0.2511, 0.0739, 1.5281], "466": [0.2408475, 0.077016, 1.4861114], "467": [0.2298512, 0.0802664, 1.4395215], "468": [0.2184072, 0.0836668, 1.3898799], "469": [0.2068115, 0.0872328, 1.3387362], "470": [0.19536, 0.09098, 1.28764], "471": [0.1842136, 0.09491755, 1.2374223], "472": [0.1733273, 0.09904584, 1.1878243], "473": [0.1626881, 0.1033674, 1.1387611], "474": [0.1522833, 0.1078846, 1.090148], "475": [0.1421, 0.1126, 1.0419], "476": [0.1321786, 0.117532, 0.9941976], "477": [0.1225696, 0.1226744, 0.9473473], "478": [0.1132752, 0.1279928, 0.9014531], "479": [0.1042979, 0.1334528, 0.8566193], "480": [0.09564, 0.13902, 0.8129501], "481": [0.08729955, 0.1446764, 0.7705173], "482": [0.07930804, 0.1504693, 0.7294448], "483": [0.07171776, 0.1564619, 0.6899136], "484": [0.06458099, 0.1627177, 0.6521049], "485": [0.05795001, 0.1693, 0.6162], "486": [0.05186211, 0.1762431, 0.5823286], "487": [0.04628152, 0.1835581, 0.5504162], "488": [0.04115088, 0.1912735, 0.5203376], "489": [0.03641283, 0.199418, 0.4919673], "490": [0.03201, 0.20802, 0.46518], "491": [0.0279172, 0.2171199, 0.4399246], "492": [0.0241444, 0.2267345, 0.4161836], "493": [0.020687, 0.2368571, 0.3938822], "494": [0.0175404, 0.2474812, 0.3729459], "495": [0.0147, 0.2586, 0.3533], "496": [0.01216179, 0.2701849, 0.3348578], "497": [0.00991996, 0.2822939, 0.3175521], "498": [0.00796724, 0.2950505, 0.3013375], "499": [0.006296346, 0.308578, 0.2861686], "500": [0.0049, 0.323, 0.272], "501": [0.003777173, 0.3384021, 0.2588171], "502": [0.00294532, 0.3546858, 0.2464838], "503": [0.00242488, 0.3716986, 0.2347718], "504": [0.002236293, 0.3892875, 0.2234533], "505": [0.0024, 0.4073, 0.2123], "506": [0.00292552, 0.4256299, 0.2011692], "507": [0.00383656, 0.4443096, 0.1901196], "508": [0.00517484, 0.4633944, 0.1792254], "509": [0.00698208, 0.4829395, 0.1685608], "510": [0.0093, 0.503, 0.1582], "511": [0.01214949, 0.5235693, 0.1481383], "512": [0.01553588, 0.544512, 0.1383758], "513": [0.01947752, 0.56569, 0.1289942], "514": [0.02399277, 0.5869653, 0.1200751], "515": [0.0291, 0.6082, 0.1117], "516": [0.03481485, 0.6293456, 0.1039048], "517": [0.04112016, 0.6503068, 0.09666748], "518": [0.04798504, 0.6708752, 0.08998272], "519": [0.05537861, 0.6908424, 0.08384531], "520": [0.06327, 0.71, 0.07824999], "521": [0.07163501, 0.7281852, 0.07320899], "522": [0.08046224, 0.7454636, 0.06867816], "523": [0.08973996, 0.7619694, 0.06456784], "524": [0.09945645, 0.7778368, 0.06078835], "525": [0.1096, 0.7932, 0.05725001], "526": [0.1201674, 0.8081104, 0.05390435], "527": [0.1311145, 0.8224962, 0.05074664], "528": [0.1423679, 0.8363068, 0.04775276], "529": [0.1538542, 0.8494916, 0.04489859], "530": [0.1655, 0.862, 0.04216], "531": [0.1772571, 0.8738108, 0.03950728], "532": [0.18914, 0.8849624, 0.03693564], "533": [0.2011694, 0.8954936, 0.03445836], "534": [0.2133658, 0.9054432, 0.03208872], "535": [0.2257499, 0.9148501, 0.02984], "536": [0.2383209, 0.9237348, 0.02771181], "537": [0.2510668, 0.9320924, 0.02569444], "538": [0.2639922, 0.9399226, 0.02378716], "539": [0.2771017, 0.9472252, 0.02198925], "540": [0.2904, 0.954, 0.0203], "541": [0.3038912, 0.9602561, 0.01871805], "542": [0.3175726, 0.9660074, 0.01724036], "543": [0.3314384, 0.9712606, 0.01586364], "544": [0.3454828, 0.9760225, 0.01458461], "545": [0.3597, 0.9803, 0.0134], "546": [0.3740839, 0.9840924, 0.01230723], "547": [0.3886396, 0.9874182, 0.01130188], "548": [0.4033784, 0.9903128, 0.01037792], "549": [0.4183115, 0.9928116, 0.009529306], "550": [0.4334499, 0.9949501, 0.008749999], "551": [0.4487953, 0.9967108, 0.0080352], "552": [0.464336, 0.9980983, 0.0073816], "553": [0.480064, 0.999112, 0.0067854], "554": [0.4959713, 0.9997482, 0.0062428], "555": [0.5120501, 1.0, 0.005749999], "556": [0.5282959, 0.9998567, 0.0053036], "557": [0.5446916, 0.9993046, 0.0048998], "558": [0.5612094, 0.9983255, 0.0045342], "559": [0.5778215, 0.9968987, 0.0042024], "560": [0.5945, 0.995, 0.0039], "561": [0.6112209, 0.9926005, 0.0036232], "562": [0.6279758, 0.9897426, 0.0033706], "563": [0.6447602, 0.9864444, 0.0031414], "564": [0.6615697, 0.9827241, 0.0029348], "565": [0.6784, 0.9786, 0.002749999], "566": [0.6952392, 0.9740837, 0.0025852], "567": [0.7120586, 0.9691712, 0.0024386], "568": [0.7288284, 0.9638568, 0.0023094], "569": [0.7455188, 0.9581349, 0.0021968], "570": [0.7621, 0.952, 0.0021], "571": [0.7785432, 0.9454504, 0.002017733], "572": [0.7948256, 0.9384992, 0.0019482], "573": [0.8109264, 0.9311628, 0.0018898], "574": [0.8268248, 0.9234576, 0.001840933], "575": [0.8425, 0.9154, 0.0018], "576": [0.8579325, 0.9070064, 0.001766267], "577": [0.8730816, 0.8982772, 0.0017378], "578": [0.8878944, 0.8892048, 0.0017112], "579": [0.9023181, 0.8797816, 0.001683067], "580": [0.9163, 0.87, 0.001650001], "581": [0.9297995, 0.8598613, 0.001610133], "582": [0.9427984, 0.849392, 0.0015644], "583": [0.9552776, 0.838622, 0.0015136], "584": [0.9672179, 0.8275813, 0.001458533], "585": [0.9786, 0.8163, 0.0014], "586": [0.9893856, 0.8047947, 0.001336667], "587": [0.9995488, 0.793082, 0.00127], "588": [1.0090892, 0.781192, 0.001205], "589": [1.0180064, 0.7691547, 0.001146667], "590": [1.0263, 0.757, 0.0011], "591": [1.0339827, 0.7447541, 0.0010688], "592": [1.040986, 0.7324224, 0.0010494], "593": [1.047188, 0.7200036, 0.0010356], "594": [1.0524667, 0.7074965, 0.0010212], "595": [1.0567, 0.6949, 0.001], "596": [1.0597944, 0.6822192, 0.00096864], "597": [1.0617992, 0.6694716, 0.
00092992], "598": [1.0628068, 0.6566744, 0.00088688], "599": [1.0629096, 0.6438448, 0.00084256], "600": [1.0622, 0.631, 0.0008], "601": [1.0607352, 0.6181555, 0.00076096], "602": [1.0584436, 0.6053144, 0.00072368], "603": [1.0552244, 0.5924756, 0.00068592], "604": [1.0509768, 0.5796379, 0.00064544], "605": [1.0456, 0.5668, 0.0006], "606": [1.0390369, 0.5539611, 0.0005478667], "607": [1.0313608, 0.5411372, 0.0004916], "608": [1.0226662, 0.5283528, 0.0004354], "609": [1.0130477, 0.5156323, 0.0003834667], "610": [1.0026, 0.503, 0.00034], "611": [0.9913675, 0.4904688, 0.0003072533], "612": [0.9793314, 0.4780304, 0.00028316], "613": [0.9664916, 0.4656776, 0.00026544], "614": [0.9528479, 0.4534032, 0.0002518133], "615": [0.9384, 0.4412, 0.00024], "616": [0.923194, 0.42908, 0.0002295467], "617": [0.907244, 0.417036, 0.00022064], "618": [0.890502, 0.405032, 0.00021196], "619": [0.87292, 0.393032, 0.0002021867], "620": [0.8544499, 0.381, 0.00019], "621": [0.835084, 0.3689184, 0.0001742133], "622": [0.814946, 0.3568272, 0.00015564], "623": [0.794186, 0.3447768, 0.00013596], "624": [0.772954, 0.3328176, 0.0001168533], "625": [0.7514, 0.321, 0.0001], "626": [0.7295836, 0.3093381, 8.613333e-05], "627": [0.7075888, 0.2978504, 7.46e-05], "628": [0.6856022, 0.2865936, 6.5e-05], "629": [0.6638104, 0.2756245, 5.693333e-05], "630": [0.6424, 0.265, 4.999999e-05], "631": [0.6215149, 0.2547632, 4.416e-05], "632": [0.6011138, 0.2448896, 3.948e-05], "633": [0.5811052, 0.2353344, 3.572e-05], "634": [0.5613977, 0.2260528, 3.264e-05], "635": [0.5419, 0.217, 3e-05], "636": [0.5225995, 0.2081616, 2.765333e-05], "637": [0.5035464, 0.1995488, 2.556e-05], "638": [0.4847436, 0.1911552, 2.364e-05], "639": [0.4661939, 0.1829744, 2.181333e-05], "640": [0.4479, 0.175, 2e-05], "641": [0.4298613, 0.1672235, 1.813333e-05], "642": [0.412098, 0.1596464, 1.62e-05], "643": [0.394644, 0.1522776, 1.42e-05], "644": [0.3775333, 0.1451259, 1.213333e-05], "645": [0.3608, 0.1382, 1e-05], "646": [0.3444563, 0.1315003, 7.733333e-06], "647": [0.3285168, 0.1250248, 5.4e-06], "648": [0.3130192, 0.1187792, 3.2e-06], "649": [0.2980011, 0.1127691, 1.333333e-06], "650": [0.2835, 0.107, 0.0], "651": [0.2695448, 0.1014762, 0.0], "652": [0.2561184, 0.09618864, 0.0], "653": [0.2431896, 0.09112296, 0.0], "654": [0.2307272, 0.08626485, 0.0], "655": [0.2187, 0.0816, 0.0], "656": [0.2070971, 0.07712064, 0.0], "657": [0.1959232, 0.07282552, 0.0], "658": [0.1851708, 0.06871008, 0.0], "659": [0.1748323, 0.06476976, 0.0], "660": [0.1649, 0.061, 0.0], "661": [0.1553667, 0.05739621, 0.0], "662": [0.14623, 0.05395504, 0.0], "663": [0.13749, 0.05067376, 0.0], "664": [0.1291467, 0.04754965, 0.0], "665": [0.1212, 0.04458, 0.0], "666": [0.1136397, 0.04175872, 0.0], "667": [0.106465, 0.03908496, 0.0], "668": [0.09969044, 0.03656384, 0.0], "669": [0.09333061, 0.03420048, 0.0], "670": [0.0874, 0.032, 0.0], "671": [0.08190096, 0.02996261, 0.0], "672": [0.07680428, 0.02807664, 0.0], "673": [0.07207712, 0.02632936, 0.0], "674": [0.06768664, 0.02470805, 0.0], "675": [0.0636, 0.0232, 0.0], "676": [0.05980685, 0.02180077, 0.0], "677": [0.05628216, 0.02050112, 0.0], "678": [0.05297104, 0.01928108, 0.0], "679": [0.04981861, 0.01812069, 0.0], "680": [0.04677, 0.017, 0.0], "681": [0.04378405, 0.01590379, 0.0], "682": [0.04087536, 0.01483718, 0.0], "683": [0.03807264, 0.01381068, 0.0], "684": [0.03540461, 0.01283478, 0.0], "685": [0.0329, 0.01192, 0.0], "686": [0.03056419, 0.01106831, 0.0], "687": [0.02838056, 0.01027339, 0.0], "688": [0.02634484, 0.009533311, 0.0], "689": [0.02445275, 0.008846157, 0.0], "690": [0.0227, 0.00821, 0.0], "691": [0.02108429, 0.007623781, 0.0], "692": [0.01959988, 0.007085424, 0.0], "693": [0.01823732, 0.006591476, 0.0], "694": [0.01698717, 0.006138485, 0.0], "695": [0.01584, 0.005723, 0.0], "696": [0.01479064, 0.005343059, 0.0], "697": [0.01383132, 0.004995796, 0.0], "698": [0.01294868, 0.004676404, 0.0], "699": [0.0121292, 0.004380075, 0.0], "700": [0.01135916, 0.004102, 0.0], "701": [0.01062935, 0.003838453, 0.0], "702": [0.009938846, 0.003589099, 0.0], "703": [0.009288422, 0.003354219, 0.0], "704": [0.008678854, 0.003134093, 0.0], "705": [0.008110916, 0.002929, 0.0], "706": [0.007582388, 0.002738139, 0.0], "707": [0.007088746, 0.002559876, 0.0], "708": [0.006627313, 0.002393244, 0.0], "709": [0.006195408, 0.002237275, 0.0], "710": [0.005790346, 0.002091, 0.0], "711": [0.005409826, 0.001953587, 0.0], "712": [0.005052583, 0.00182458, 0.0], "713": [0.004717512, 0.00170358, 0.0], "714": [0.004403507, 0.001590187, 0.0], "715": [0.004109457, 0.001484, 0.0], "716": [0.003833913, 0.001384496, 0.0], "717": [0.003575748, 0.001291268, 0.0], "718": [0.003334342, 0.001204092, 0.0], "719": [0.003109075, 0.001122744, 0.0], "720": [0.002899327, 0.001047, 0.0], "721": [0.002704348, 0.0009765896, 0.0], "722": [0.00252302, 0.0009111088, 0.0], "723": [0.002354168, 0.0008501332, 0.0], "724": [0.002196616, 0.0007932384, 0.0], "725": [0.00204919, 0.00074, 0.0], "726": [0.00191096, 0.0006900827, 0.0], "727": [0.001781438, 0.00064331, 0.0], "728": [0.00166011, 0.000599496, 0.0], "729": [0.001546459, 0.0005584547, 0.0], "730": [0.001439971, 0.00052, 0.0], "731": [0.001340042, 0.0004839136, 0.0], "732": [0.001246275, 0.0004500528, 0.0], "733": [0.001158471, 0.0004183452, 0.0], "734": [0.00107643, 0.0003887184, 0.0], "735": [0.0009999493, 0.0003611, 0.0], "736": [0.0009287358, 0.0003353835, 0.0], "737": [0.0008624332, 0.0003114404, 0.0], "738": [0.0008007503, 0.0002891656, 0.0], "739": [0.000743396, 0.0002684539, 0.0], "740": [0.0006900786, 0.0002492, 0.0], "741": [0.0006405156, 0.0002313019, 0.0], "742": [0.0005945021, 0.0002146856, 0.0], "743": [0.0005518646, 0.0001992884, 0.0], "744": [0.000512429, 0.0001850475, 0.0], "745": [0.0004760213, 0.0001719, 0.0], "746": [0.0004424536, 0.0001597781, 0.0], "747": [0.0004115117, 0.0001486044, 0.0], "748": [0.0003829814, 0.0001383016, 0.0], "749": [0.0003566491, 0.0001287925, 0.0], "750": [0.0003323011, 0.00012, 0.0], "751": [0.0003097586, 0.0001118595, 0.0], "752": [0.0002888871, 0.0001043224, 0.0], "753": [0.0002695394, 9.73356e-05, 0.0], "754": [0.0002515682, 9.084587e-05, 0.0], "755": [0.0002348261, 8.48e-05, 0.0], "756": [0.000219171, 7.914667e-05, 0.0], "757": [0.0002045258, 7.3858e-05, 0.0], "758": [0.0001908405, 6.8916e-05, 0.0], "759": [0.0001780654, 6.430267e-05, 0.0], "760": [0.0001661505, 6e-05, 0.0], "761": [0.0001550236, 5.598187e-05, 0.0], "762": [0.0001446219, 5.22256e-05, 0.0], "763": [0.0001349098, 4.87184e-05, 0.0], "764": [0.000125852, 4.544747e-05, 0.0], "765": [0.000117413, 4.24e-05, 0.0], "766": [0.0001095515, 3.956104e-05, 0.0], "767": [0.0001022245, 3.691512e-05, 0.0], "768": [9.539445e-05, 3.444868e-05, 0.0], "769": [8.90239e-05, 3.214816e-05, 0.0], "770": [8.307527e-05, 3e-05, 0.0], "771": [7.751269e-05, 2.799125e-05, 0.0], "772": [7.231304e-05, 2.611356e-05, 0.0], "773": [6.745778e-05, 2.436024e-05, 0.0], "774": [6.292844e-05, 2.272461e-05, 0.0], "775": [5.870652e-05, 2.12e-05, 0.0], "776": [5.477028e-05, 1.977855e-05, 0.0], "777": [5.109918e-05, 1.845285e-05, 0.0], "778": [4.767654e-05, 1.721687e-05, 0.0], "779": [4.448567e-05, 1.606459e-05, 0.0], "780": [4.150994e-05, 1.499e-05, 0.0], "781": [3.873324e-05, 1.398728e-05, 0.0], "782": [3.614203e-05, 1.305155e-05, 0.0], "783": [3.372352e-05, 1.217818e-05, 0.0], "784": [3.146487e-05, 1.136254e-05, 0.0], "785": [2.935326e-05, 1.06e-05, 0.0], "786": [2.737573e-05, 9.885877e-06, 0.0], "787": [2.552433e-05, 9.217304e-06, 0.0], "788": [2.379376e-05, 8.592362e-06, 0.0], "789": [2.21787e-05, 8.009133e-06, 0.0], "790": [2.067383e-05, 7.4657e-06, 0.0], "791": [1.927226e-05, 6.959567e-06, 0.0], "792": [1.79664e-05, 6.487995e-06, 0.0], "793": [1.674991e-05, 6.048699e-06, 0.0], "794": [1.561648e-05, 5.639396e-06, 0.0], "795": [1.455977e-05, 5.2578e-06, 0.0], "796": [1.357387e-05, 4.901771e-06, 0.0], "797": [1.265436e-05, 4.56972e-06, 0.0], "798": [1.179723e-05, 4.260194e-06, 0.0], "799": [1.099844e-05, 3.971739e-06, 0.0], "800": [1.025398e-05, 3.7029e-06, 0.0], "801": [9.559646e-06, 3.452163e-06, 0.0], "802": [8.912044e-06, 3.218302e-06, 0.0], "803": [8.308358e-06, 3.0003e-06, 0.0], "804": [7.745769e-06, 2.797139e-06, 0.0], "805": [7.221456e-06, 2.6078e-06, 0.0], "806": [6.732475e-06, 2.43122e-06, 0.0], "807": [6.276423e-06, 2.266531e-06, 0.0], "808": [5.851304e-06, 2.113013e-06, 0.0], "809": [5.455118e-06, 1.969943e-06, 0.0], "810": [5.085868e-06, 1.8366e-06, 0.0], "811": [4.741466e-06, 1.71223e-06, 0.0], "812": [4.420236e-06, 1.596228e-06, 0.0], "813": [4.120783e-06, 1.48809e-06, 0.0], "814": [3.841716e-06, 1.387314e-06, 0.0], "815": [3.581652e-06, 1.2934e-06, 0.0], "816": [3.339127e-06, 1.20582e-06, 0.0], "817": [3.112949e-06, 1.124143e-06, 0.0], "818": [2.902121e-06, 1.048009e-06, 0.0], "819": [2.705645e-06, 9.77058e-07, 0.0], "820": [2.522525e-06, 9.1093e-07, 0.0], "821": [2.351726e-06, 8.49251e-07, 0.0], "822": [2.192415e-06, 7.91721e-07, 0.0], "823": [2.043902e-06, 7.3809e-07, 0.0], "824": [1.905497e-06, 6.8811e-07, 0.0], "825": [1.776509e-06, 6.4153e-07, 0.0], "826": [1.656215e-06, 5.9809e-07, 0.0], "827": [1.544022e-06, 5.57575e-07, 0.0], "828": [1.43944e-06, 5.19808e-07, 0.0], "829": [1.341977e-06, 4.84612e-07, 0.0], "830": [1.251141e-06, 4.5181e-07, 0.0]}
Code used to generate the correspondence table between blackbody temperature and RGB value
in the generated csv file, the first column is the blackbody temperature, and the second / third / fourth column is the r/g/b value respectively, with a range of [0,1]
# Establish the mapping table between blackbody temperature and RGB color
from calculateColour import bb_temperature_to_RGB
import numpy as np
import csv
T_list = np.arange(200, 100001, 10)
r_list = []
g_list = []
b_list = []
for T in T_list:
if(T % 2000 == 0):
print(T)
RGB = bb_temperature_to_RGB(T)
r = RGB[0]
g = RGB[1]
b = RGB[2]
r_list.append(r)
g_list.append(g)
b_list.append(b)
with open("TCTable.csv", "w") as f:
spamwriter = csv.writer(f, delimiter=",")
for idx in range(len(T_list)):
spamwriter.writerow([T_list[idx], r_list[idx], g_list[idx], b_list[idx]])