Detailed explanation and summary of the real topic of the 12th Blue Bridge Cup Java group B provincial competition in 2021 [the first provincial competition 2021.04.18]

This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.

[answer]: 76

Solution 1: ASCII calculation

[analysis]: count back from A.

package provincialGames_12_2021_1_JavaB;

public class A01_ASC { // 76
	public static void main(String[] args) {
		System.out.println('A' - 0); // 65
		System.out.println('B' - 0); // 66
		System.out.println('L' - 0); // 76
		System.out.println('Z' - 0); // 90
		System.out.println(65 + 'L' - 'A'); // 76
		System.out.println((int) 'L'); // 76
	}
}

Solution 2: Call of class

package provincialGames_12_2021_1_JavaB;

public class A01_ASC2 { // 76
	public static void main(String[] args) {
		new A01_ASC2().run();
	}

	void run() {
		System.out.println(65 + 'L' - 'A'); // 76
		System.out.println((int) 'L'); // 76
	}
}

2, Question B: card

Total score of this question: 5 points

[problem description]

Xiaolan has many digital cards, each with numbers 0 to 9.

Xiaolan is going to use these cards to spell some numbers. He wants to spell positive integers from 1. Each time he spell one, he will save it. The card can't be used to spell other numbers.

Xiaolan wants to know how much she can spell from 1.

For example, when Xiaolan has 30 cards, including 3 from 0 to 9, Xiaolan can spell 1 to 10,

But when you spell 11, there is only one card 1, which is not enough to spell 11.

Now Xiaolan has 2021 cards from 0 to 9, a total of 20210. How many can Xiaolan spell from 1?

Tip: it is recommended to use computer programming to solve the problem.

[answer submission]

[answer]: 3181

Solution 1: Enumeration

[parse]: enumerate from 1 onwards.

package provincialGames_12_2021_1_JavaB;

public class B02_card { // 3181
	public static int arr[] = new int[10];

	public static boolean del(int x) {
		while (x != 0) {
			arr[x % 10]--;
			if (arr[x % 10] < 0)
				return false;
			x /= 10;
		}
		return true;
	}

	public static void main(String[] args) {
		for (int i = 0; i < 10; i++)
			arr[i] = 2021;
		for (int i = 1; i < 5000; i++) {
			if (!del(i)) {
				System.out.println(i - 1); // 3181
				break;
			}
		}
	}
}

Solution 2: simple solution

package provincialGames_12_2021_1_JavaB;

public class B02_Card 2 { // 3181
	public static void main(String[] args) {
		new B02_Card 2().run();
	}

	void run() {
		System.out.println(calc(2021)); // 3181
	}

	int calc(int upper) {
		int[] count = new int[10];
		for (int n = 1, k = 1;; k = ++n)
			do {
				if (++count[k % 10] > upper)
					return n - 1;
			} while ((k /= 10) > 0);
	}
}

Solution 3: overtaking in curve

[analysis]: observe the occurrence of [0,9] in the interval [1,9]. In [1,9], 1 to 9 appear once each.

Expand the scope of observation to [1,99], 10 times for 1 of the 10th place [10,19], 10 times for 2 of the 10th place [20,29], 10 times for 9 of the 10th place [90,99], 10 times for low position [0,9], 20 times for 1 to 9, and 9 times for 0.

If you continue to expand the observation range, you will find that the use times of 1 are always no less than 0, 2 to 9, that is, statistics of 0, 2 to 9 are meaningless.

package provincialGames_12_2021_1_JavaB;

public class B02_Card 3 { // 3181
	public static void main(String[] args) {
		new B02_Card 3().run();
	}

	void run() {
		System.out.println(calc(20)); // 99
	}

	int calc(int upper) {
		int count = 0;
		for (int n = 1, k = 1;; k = ++n) {
			do
				if (k % 10 == 1)
					count++;
			while ((k /= 10) > 0);
			if (count > upper)
				return n - 1;
		}
	}
}

3, Question C: straight line

Total score of this question: 10 points

[problem description]

In the plane rectangular coordinate system, two points can determine a straight line. If there are multiple points on a straight line, the straight line determined by any two of these points is the same.

2 on a given plane × Three integer points {(x, y)|0 ≤ x < 2, 0 ≤ y < 3, X ∈ Z, y ∈ Z}, i.e. points where the abscissa is an integer between 0 and 1 (including 0 and 1) and the ordinate is an integer between 0 and 2 (including 0 and 2). These points determine a total of 11 different lines.

20 on a given plane × 21 integer points {(x, y)|0 ≤ x < 20, 0 ≤ y < 21, X ∈ Z, y ∈ Z}, that is, points where the abscissa is an integer between 0 and 19 (including 0 and 19) and the ordinate is an integer between 0 and 20 (including 0 and 20). How many different straight lines are determined by these points.

[answer submission]

[answer]: 40257

Solution 1: set of linear equations

[analysis]: use: y=kx+b as straight line expression. Once k and b are determined, the straight line is determined. All data can be counted and de duplicated.

A simple idea is to connect all points, remove duplicate lines, and then count.

In order to facilitate the representation, the oblique section equation y=kx+b is used to represent each straight line, where k is the slope of the straight line and b is the intercept of the straight line on the y-axis. The lines with no slope are not treated uniformly, and a 20 is added to the result.

be careful! The result of this procedure is inaccurate.

package provincialGames_12_2021_1_JavaB;

import java.util.HashSet;
import java.util.Set;

public class C03_straight line { // 40257
	public static void main(String[] args) {
		new C03_straight line().run();
	}

	int X = 20, Y = 21;

	void run() {
		Set<Line> set = new HashSet();
		for (int x1 = 0; x1 < X; x1++)
			for (int y1 = 0; y1 < Y; y1++)
				for (int x2 = x1; x2 < X; x2++)
					for (double y2 = 0; y2 < Y; y2++)
						if (x1 != x2) {
							double k = (y2 - y1) / (x2 - x1);
							double b = -x1 * k + y1;
							set.add(new Line(k, b));
						}
		System.out.println(set.size() + X); // 41255
	}

	class Line {
		double k, b;

		Line(double b, double k) {
			this.k = k;
			this.b = b;
		}

		@Override
		public boolean equals(Object obj) {
			return k == ((Line) obj).k && b == ((Line) obj).b;
		}

		@Override
		public int hashCode() {
			return (int) k ^ (int) b;
		}
	}
}

Solution 2: fraction elimination error

[analysis]: when the slope is represented by floating-point numbers, the accuracy is uneven. It is true that the error can be limited to a range. When the absolute difference falls into it, we regard it as the same value. However, when the representable range is small, we can define the fraction to achieve no error, rather than control the accuracy.

package provincialGames_12_2021_1_JavaB;

import java.util.HashSet;
import java.util.Set;

public class C03_Straight line 2 { // 40257
	public static void main(String[] args) {
		new C03_Straight line 2().run();
	}

	int X = 20, Y = 21;

	void run() {
		Set<Line> set = new HashSet();
		for (int x1 = 0; x1 < X; x1++)
			for (int y1 = 0; y1 < Y; y1++)
				for (int x2 = x1; x2 < X; x2++)
					for (int y2 = 0; y2 < Y; y2++)
						if (x1 != x2) {
							Fraction k = new Fraction(y2 - y1, x2 - x1);
							Fraction b = new Fraction(y1 * (x2 - x1) - x1 * (y2 - y1), x2 - x1);
							set.add(new Line(k, b));
						}
		System.out.println(set.size() + X); // 40257
	}

	class Fraction {
		int numerator, denominator;

		Fraction(int numerator, int denominator) {
			int gcd = gcd(numerator, denominator);
			this.denominator = denominator / gcd;
			this.numerator = numerator / gcd;
		}

		int gcd(int a, int b) {
			return b == 0 ? a : gcd(b, a % b);
		}

		@Override
		public boolean equals(Object obj) {
			return this.numerator == ((Fraction) obj).numerator && this.denominator == ((Fraction) obj).denominator;
		}
	}

	class Line {
		Fraction k, b;

		Line(Fraction b, Fraction k) {
			this.k = k;
			this.b = b;
		}

		@Override
		public boolean equals(Object obj) {
			return this.k.equals(((Line) obj).k) && this.b.equals(((Line) obj).b);
		}

		@Override
		public int hashCode() {
			return k.denominator;
		}
	}
}

Solution 3: plane geometry

[analysis]: This is a plane rectangular coordinate system, and the origin and (1,2) are connected into a line segment.

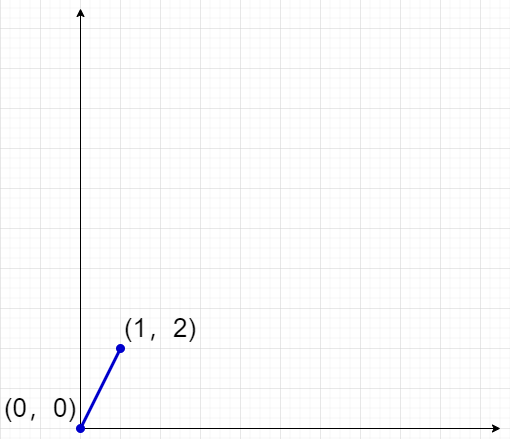
We will mark the straight line passing through these two points, and the point through which this straight line passes and the vertical line of this point on the horizontal and vertical axis.

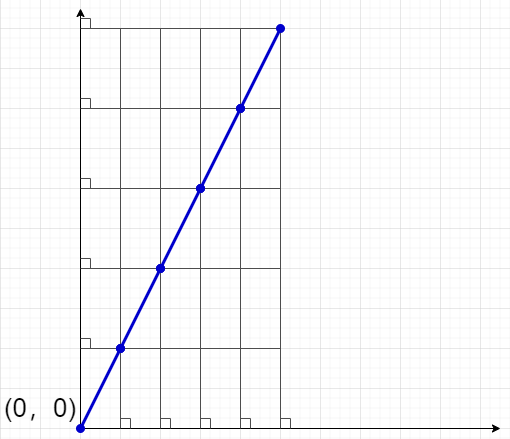
Obviously, if a straight line passes through two points (x1, Y1) and (X2, Y2), it must also pass through (x1 + k(x1 − x2), y1 + k(y1 − y2)), k ∈ Z.

If we mark the points that all lines pass through when connecting a straight line, we can skip directly when we encounter the marked two points next time.

package provincialGames_12_2021_1_JavaB;

public class C03_Straight line 3 { // 40257
	public static void main(String[] args) {
		new C03_Straight line 3().run();
	}

	int X = 20, Y = 21;

	void run() {
		int count = 0;
		boolean[][][][] marked = new boolean[X][Y][X][Y];
		for (int x1 = 0; x1 < X; x1++)
			for (int y1 = 0; y1 < Y; y1++) {
				marked[x1][y1][x1][y1] = true;
				for (int x2 = 0; x2 < X; x2++)
					for (int y2 = 0; y2 < Y; y2++) {
						if (marked[x1][y1][x2][y2])
							continue;
						int x = x1, y = y1, xOffset = x - x2, yOffset = y - y2;
						while (x >= 0 && x < X && y >= 0 && y < Y) {
							x += xOffset;
							y += yOffset;
						}
						x -= xOffset;
						y -= yOffset;
						while (x >= 0 && x < X && y >= 0 && y < Y) {
							for (int i = x - xOffset, j = y - yOffset; i >= 0 && i < X && j >= 0
									&& j < Y; i -= xOffset, j -= yOffset) {
								marked[x][y][i][j] = marked[i][j][x][y] = true;
							}
							x -= xOffset;
							y -= yOffset;
						}
						count++;
					}
			}
		System.out.println(count); // 40257
	}
}

4, Question D: goods placement

Total score of this question: 10 points

[problem description]

Xiaolan has a large warehouse, which can put a lot of goods.

Now, Xiaolan has n boxes of goods to be placed in the warehouse, and each box of goods is a regular cube. Xiaolan stipulates three mutually perpendicular directions of length, width and height. The side of each box of goods must be strictly parallel to the length, width and height.

Xiaolan hopes that all the goods will eventually be placed into a big cube. That is, pile L, W and H goods respectively in the direction of length, width and height, and meet the requirement of n = L × W × H.

Given n, how many schemes for stacking goods meet the requirements.

For example, when n = 4, there are six schemes: 1 × one × 4,1 × two × 2,1 × four × 1,2 × one × 2,2 × two × 1,4 × one × 1.

How many schemes are there when n = 2021041820210418 (note that there are 16 digits)?

Tip: it is recommended to use computer programming to solve the problem.

[answer submission]

[answer]: 2430

Solution 1: violent search

[analysis]: enumerate the divisors of 2021041820210418 and enumerate the divisors in multiple cycles; The answer can be obtained by fully arranging the three enumerated numbers.

Basic arithmetic theorems that must be tested in each session.

It's not impossible to set two for directly, but the program written in this way usually can't run until the end of the game.

Therefore, we should avoid the judgment of invalid factors. Here, the statistics is that the qualitative factor is divided into three parts and the number of possible combinations, which is equivalent to the original proposition.

There's nothing to say. Only two sets of for are used because the factors of a number can only appear in pairs. Sweep the number blindness.

package provincialGames_12_2021_1_JavaB;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;

public class D04_Cargo placement { // 2430
	public static void main(String[] args) {
		new D04_Cargo placement().run();
	}

	long n = 2021041820210418L;

	void run() {
		List<Integer> exps0 = new ArrayList();
		ArrayDeque<Integer> exps1 = new ArrayDeque();
		for (int k = 2; k <= n; k++)
			if (n % k == 0) {
				int e = 0;
				while (n % k == 0) {
					n /= k;
					e++;
				}
				exps0.add(e);
			}
		System.out.println(dfs(exps0, exps1, 0)); // 2430
	}

	int dfs(List<Integer> exps0, ArrayDeque<Integer> exps1, int cur) {
		if (cur == exps0.size()) {
			int comb = 1;
			for (int exp : exps1)
				comb *= exp + 1;
			return comb;
		}
		int ans = 0;
		for (int i = exps0.get(cur); i >= 0; i--) {
			exps1.push(i);
			ans += dfs(exps0, exps1, cur + 1);
			exps1.pop();
		}
		return ans;
	}
}

Solution 2: scaling quality factor

[analysis]: for example,

When n=9 °, there are six schemes: 1 × one × 9,1 × three × 3,1 × nine × 1,3 × one × 3,3 × three × 1,9 × one × 1；

When n=25, there are six schemes: 1 × one × 25,1 × five × 5,⋯；

When n=p^2, there are six schemes: 1 × one × p^2,1 × p × p,⋯； Where p is a prime number.

In fact, in the solution of the above example, we can find that the number of combinations has nothing to do with its specific value, it is only linked to the quality factor index.

2021041820210418 = 2 × 3^3 × 17 × 131 × 2857 × 5882353

If we replace them with the smallest prime numbers, we get the new number 2 ^ 3 × three × five × seven × eleven × 13 = 120120 and 2021041820210418 are equivalent under this proposition. The size of 120120 is enough. We found all the factors of it.

package provincialGames_12_2021_1_JavaB;

import java.util.ArrayList;
import java.util.List;

public class D04_Cargo placement 2 { // 2430
	public static void main(String[] args) {
		new D04_Cargo placement 2().run();
	}

	long N = 2021041820210418L;

	void run() {
		List<Integer> exps = new ArrayList();
		for (int k = 2; k <= N; k++)
			if (N % k == 0) {
				int e = 0;
				while (N % k == 0) {
					N /= k;
					e++;
				}
				exps.add(e);
			}
		exps.sort((a, b) -> (b - a));
		int n = 1, p = 2, ans = 0;
		for (int exp : exps) {
			for (int i = 2; i * i <= p; i++)
				if (p % i == 0) {
					i = 1;
					p++;
				}
			while (exp-- > 0)
				n *= p;
			p++;
		}
		for (int a = 1; a <= n; a++)
			if (n % a == 0)
				for (int b = 1; b <= n; b++)
					if (n / a % b == 0)
						ans++;
		System.out.println(ans); // 2430
	}
}

5, Question E: Path

Total score of this question: 15 points

[problem description]

Xiaolan is very happy after learning the shortest path. He defines a special graph and hopes to find the shortest path in the graph.

The diagram of Xiaolan consists of 2021 nodes, numbered from 1 to 2021.

For two different nodes a and b, if the absolute value of the difference between a and b is greater than 21, there is no edge connection between the two nodes; If the absolute value of the difference between a and b is less than or equal to 21, there is an undirected edge with a length of the least common multiple of a and b.

For example, there is no edge connection between node 1 and node 23; There is an undirected edge between node 3 and node 24, with a length of 24; There is an undirected edge between node 15 and node 25, with a length of 75.

Please calculate the shortest path length between node 1 and node 2021.

Tip: it is recommended to use computer programming to solve the problem.

[answer submission]

[answer]: 10266837

Solution 1: Search

[analysis]: DP idea: from 2 to 2021, each position comes from its previous 21 positions, and the minimum value of 21 data can be obtained.

The topic has been made clear enough to build one with 2021 vertices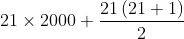For an undirected graph with edges, the algorithm on the running graph is finished.

In addition, the detail is whether the shaping will overflow. We take the largest prime number 2017 in [12021] and multiply it by 2021 ^ 2, and the result is a little exaggerated. Although after testing, the possible line weight combination will not exceed 2 ^ 31-1 at most, it is more cost-effective to directly use long shaping because it is oriented to the competition and considering the time cost of screening.

Depth first search: 2021 vertices, most of which are connected to 2 × 21 sides, don't search deeply. One search is completion completed successfully in 500ms (4 hour ago). The computer is facing the player and goes to jail.

Memory search:

In depth first search, when searching for the optimal result, it is usually necessary to completely enumerate all possible problem states.
However, in the set of problem States, the "suffix" of all options is the same, that is, all optional branches end with the same node.
If we save the shortest path from the searched node to the target node, we will return directly when we search the branch of this "suffix" again.
Then the problem may be solved in a short time. This is also called memory search.

package provincialGames_12_2021_1_JavaB;

import java.util.ArrayList;
import java.util.List;

public class E05_route { // 10266837
	public static void main(String[] args) {
		new E05_route().run();
	}

	int N = 2021;

	int[] weight = new int[N + 1];

	List<Edge>[] graph = new List[N + 1];

	boolean[] visited = new boolean[N + 1];

	void run() {
		for (int i = 1; i <= N; i++)
			graph[i] = new ArrayList();
		for (int v = 1; v < N; v++)
			for (int w = v + 1; w <= min(v + 21, N); w++) {
				graph[v].add(new Edge(w, lcm(v, w)));
				graph[w].add(new Edge(v, lcm(v, w)));
			}
		visited[1] = true;
		System.out.println(dfs(1)); // 10266837
	}

	int dfs(int v) {
		if (v == N)
			return 0;
		if (weight[v] != 0)
			return weight[v];
		int min = 0x7FFFFFFF;
		for (Edge edge : graph[v]) {
			if (visited[edge.w])
				continue;
			visited[edge.w] = true;
			min = min(min, dfs(edge.w) + edge.weight);
			visited[edge.w] = false;
		}
		return weight[v] = min;
	}

	int min(int a, int b) {
		return a < b ? a : b;
	}

	int lcm(int a, int b) {
		return a * b / gcd(a, b);
	}

	int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}

	class Edge {
		int w, weight;

		Edge(int w, int weight) {
			this.weight = weight;
			this.w = w;
		}
	}
}

Solution 2: Search - branch cutting and wide search

[analysis]: in fact, simple search, whether deep search or wide search, is a very aggressive behavior in the competition. There are too many factors affecting the execution efficiency of these two algorithms.
Of course, if there are no other ideas, we can only be a living horse doctor. Fortunately, the results can be calculated in a very short time with a simple branch shear.

package provincialGames_12_2021_1_JavaB;

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Queue;
import java.util.List;

public class E05_Path 2 { // 10266837
	public static void main(String[] args) {
		new E05_Path 2().run();
	}

	int N = 2021;

	void run() {
		List<Edge>[] graph = new List[N + 1];
		long[] visited = new long[N + 1];
		for (int i = 1; i <= N; i++)
			graph[i] = new ArrayList();
		for (int v = 1; v < N; v++)
			for (int w = v + 1; w <= min(v + 21, N); w++) {
				graph[v].add(new Edge(w, lcm(v, w)));
				graph[w].add(new Edge(v, lcm(v, w)));
			}
		Queue<Vertex> queue = new PriorityQueue();
		Arrays.fill(visited, Long.MAX_VALUE);
		queue.offer(new Vertex(1, 0));
		Vertex V = null;
		while (queue.size() > 0) {
			V = queue.poll();
			if (V.v == N)
				break;
			if (V.weight >= visited[V.v])
				continue;
			visited[V.v] = V.weight;
			for (Edge edge : graph[V.v])
				queue.offer(new Vertex(edge.w, edge.weight + V.weight));
		}
		System.out.println(V.weight); // 10266837
	}

	int min(int a, int b) {
		return a < b ? a : b;
	}

	int lcm(int a, int b) {
		return a * b / gcd(a, b);
	}

	int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}

	class Edge {
		int w, weight;

		Edge(int w, int weight) {
			this.weight = weight;
			this.w = w;
		}
	}

	class Vertex implements Comparable<Vertex> {
		int v;
		long weight;

		Vertex(int v, long weight) {
			this.weight = weight;
			this.v = v;
		}

		@Override
		public int compareTo(Vertex V) {
			return Long.compare(this.weight, V.weight);
		}
	}
}

Solution 3: single source shortest path Dijkstra

[analysis]: the graph given in the title is obviously an undirected graph with edge weighting and non negative weight. It will be finished after running all over Dijkstra.

package provincialGames_12_2021_1_JavaB;

import java.util.PriorityQueue;
import java.util.ArrayList;
import java.util.Queue;
import java.util.List;

public class E05_Path 3 { // 10266837
	public static void main(String[] args) {
		new E05_Path 3().run();
	}

	int N = 2021;

	void run() {
		boolean[] marked = new boolean[N + 1];
		List<Edge>[] graph = new List[N + 1];
		long[] distTo = new long[N + 1];
		for (int i = 1; i <= N; i++) {
			graph[i] = new ArrayList();
			distTo[i] = Long.MAX_VALUE;
		}
		for (int v = 1; v < N; v++)
			for (int w = v + 1; w <= min(v + 21, N); w++) {
				graph[v].add(new Edge(w, lcm(v, w)));
				graph[w].add(new Edge(v, lcm(v, w)));
			}
		Queue<Vertex> queue = new PriorityQueue();
		queue.offer(new Vertex(1, distTo[1] = 0));
		while (queue.size() > 0) {
			Vertex V = queue.poll();
			if (marked[V.v])
				continue;
			marked[V.v] = true;
			for (Edge edge : graph[V.v])
				if (distTo[edge.w] > distTo[V.v] + edge.weight)
					queue.offer(new Vertex(edge.w, distTo[edge.w] = distTo[V.v] + edge.weight));
		}
		System.out.println(distTo[N]); // 10266837
	}

	int min(int a, int b) {
		return a < b ? a : b;
	}

	int lcm(int a, int b) {
		return a * b / gcd(a, b);
	}

	int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}

	class Edge {
		int w, weight;

		Edge(int w, int weight) {
			this.weight = weight;
			this.w = w;
		}
	}

	class Vertex implements Comparable<Vertex> {
		int v;
		long dist;

		Vertex(int v, long dist) {
			this.dist = dist;
			this.v = v;
		}

		@Override
		public int compareTo(Vertex V) {
			return Long.compare(this.dist, V.dist);
		}
	}
}

Solution 4: single source shortest path Floyd

[analysis]: if it is the result of the shortest path. The program of O(n^3) can be run within the competition time limit. That's just Floyd without a brain.

package provincialGames_12_2021_1_JavaB;

public class E05_Path 4 { // 10266837
	public static void main(String[] args) {
		new E05_Path 4().run();
	}

	int N = 2021;

	void run() {
		long[][] floyd = new long[N + 1][N + 1];
		for (int v = 1; v < N; v++)
			for (int w = v + 1; w <= min(N, v + 21); w++)
				floyd[v][w] = floyd[w][v] = lcm(v, w);
		for (int k = 1; k <= N; k++)
			for (int v = 1; v <= N; v++)
				if (floyd[v][k] == 0)
					continue;
				else
					for (int w = 1; w <= N; w++)
						if (floyd[k][w] == 0)
							continue;
						else if (floyd[v][w] == 0 || floyd[v][k] + floyd[k][w] < floyd[v][w])
							floyd[v][w] = floyd[v][k] + floyd[k][w];
		System.out.println(floyd[1][N]); // 10266837
	}

	long min(int a, int b) {
		return a < b ? a : b;
	}

	int lcm(int a, int b) {
		return a * b / gcd(a, b);
	}

	int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}
}

6, Question F: time display

Time limit: 1.0s memory limit: 512.0MB total score of this question: 15 points

[problem description]

Xiaolan wants to cooperate with her friends to develop a time display website. On the server, the friend has obtained the current time, which is expressed as an integer. The value is the number of milliseconds from 00:00:00 on January 1, 1970 to the current time.

Now, Xiaolan will display this time on the client. Xiaolan doesn't need to display the year, month and day. It only needs to display the hours, minutes and seconds, and milliseconds. It can be directly rounded off.

Given a time expressed as an integer, please output the hour, minute and second corresponding to this time.

[input format]

The input line contains an integer representing the time.

[output format]

Output the current time represented by hour, minute and second. The format is HH:MM:SS, where HH represents hour, the value is 0 to 23, MM represents minute, the value is 0 to 59, SS represents second, and the value is 0 to 59. When the hour, minute and second are less than two digits, the leading 0 shall be supplemented.

[example input 1] 46800999

[sample output 1] 13:00:00

[example input 2] 1618708103123

[sample output 2] 01:08:23

[evaluation case scale and agreement] for all evaluation cases, the given time is a positive integer no more than 1018.

Solution 1: simulation calculation

[analysis]: simulate the process according to the topic.

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class F06_Time display {
	public static String tos(long x) {
		if (x < 10)
			return "0" + x;
		else
			return "" + x;
	}

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		long n = sc.nextLong();
		n %= (1000 * 60 * 60 * 24);
		n /= 1000;
		System.out.println(tos(n / 3600) + ":" + tos((n / 60) % 60) + ":" + tos(n % 60));
	}
}

Solution 2: direct calculation

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class F06_Time display 3 {
	public static void main(String[] args) {
		new F06_Time display 3().run();
	}

	void run() {
		long t = new Scanner(System.in).nextLong();
		System.out.printf("%02d:%02d:%02d", t / 3600000 % 24, t / 60000 % 60, t / 1000 % 60);
	}
}

Solution 3: Java date API

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;
import java.time.LocalTime;
import java.time.format.DateTimeFormatter;

public class F06_Time display 3 {
	public static void main(String[] args) {
		new F06_Time display 3().run();
	}

	void run() {
		System.out.println(LocalTime.MIDNIGHT.plusSeconds(new Scanner(System.in).nextLong() / 1000)
				.format(DateTimeFormatter.ISO_LOCAL_TIME));
		Scanner sc = new Scanner(System.in);
		long n = sc.nextLong();
		System.out.println(LocalTime.MIDNIGHT.plusSeconds(n / 1000).format(DateTimeFormatter.ISO_LOCAL_TIME));
	}
}

7, Question G: minimum weight

Time limit: 1.0s memory limit: 512.0MB total score of this question: 20 points

[problem description]

You have a balance. Now you need to design a set of weights, so that you can use these weights to weigh any positive integer weight less than or equal to N.

How many weights should this set of weights contain at least?

Note that the weight can be placed on both sides of the balance.

[input format] the input contains a positive integer N.

[output format] output an integer representing the answer.

[sample input] 7

[sample output] 3

[example description]

The weights of the three weights are 1, 4 and 6, which can weigh all the weights from 1 to 7.

1 = 1；

2 = 6 − 4 (put 6 on one side and 4 on the other side of the balance);

3 = 4 − 1；

4 = 4；

5 = 6 − 1；

6 = 6；

7 = 1 + 6；

It is impossible to weigh all weights from 1 to 7 with less than 3 weights.

[evaluation case scale and agreement] for all evaluation cases, 1 ≤ N ≤ 1000000000.

Solution 1: ternary

[analysis]: it is found by manual enumeration that it conforms to the ternary law, so it can be calculated directly.

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class G07_Minimum weight {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		long x = sc.nextLong();
		long sum = 1, cur = 1;
		while (sum < x) {
			sum += Math.pow(3, cur);
			cur++;
		}
		System.out.println(cur);
	}
}

Solution 2: variant ternary

[analysis]: regular questions. The first game of the 12th Blue Bridge Cup 2021 provincial competition (group B of Java University)

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class G07_Minimum weight 2 {
	public static void main(String[] args) {
		new G07_Minimum weight 2().run();
	}

	void run() {
		long N = new Scanner(System.in).nextLong(), ans = 1;
		for (long pow3 = 1; pow3 < N; pow3 = pow3 * 3 + 1, ans++)
			;
		System.out.println(ans);
	}
}

8, Question H: Yang Hui triangle

Time limit: 5.0s memory limit: 512.0MB total score of this question: 20 points

[problem description]

The following figure is the famous Yang Hui triangle:

If we arrange all numbers in a row from top to bottom and from left to right, we can get the following sequence:

1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...

Given a positive integer n, what number is the first occurrence of N in the output sequence?

[input format] enter an integer N.

[output format] output an integer representing the answer.

[sample input] 6

[sample output] 13

[scale and agreement of evaluation cases] for 20% of evaluation cases, 1 ≤ N ≤ 10; For all evaluation cases, 1 ≤ N ≤ 1000000000.

Solution 1: analogy monotone sequence

[analysis]: simulate the process according to the topic.

The outermost layer of Yanghui triangle is all 1, and the second layer is the sequence of natural numbers.

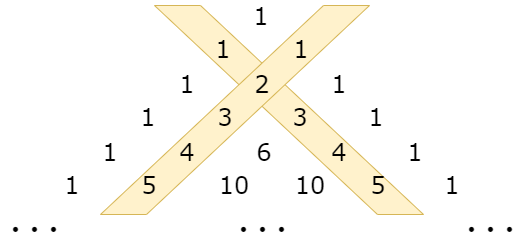
Because the Yang Hui triangle is left-right symmetrical, we can ignore the right (the numbers on the left always appear first than the right) and divide the numbers into several sequences according to layers.

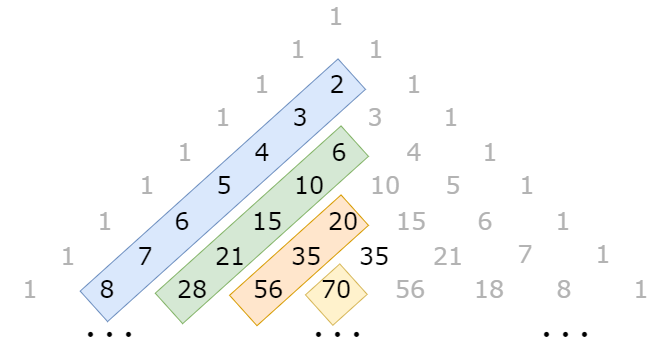
Since the sequences are incremented by single tone from the top, we can binary search the position of N on each such sequence. In particular, when N=1, we can directly output 1.

In addition, the nth row and m column of Yanghui triangle=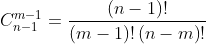, this number is growing very fast. .

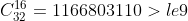That is to find the position of N in at most 14 sequences (excluding the outermost two layers), because the monotonicity of the sequence does not allow the emergence of n.

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class H08_Yang Hui triangle {
	public static void main(String[] args) {
		new H08_Yang Hui triangle().run();
	}

	int N;

	void run() {
		N = new Scanner(System.in).nextInt();
		if (N == 1)
			System.out.println(1);
		else {
			long ans = (N + 1L) * N / 2 + 2;
			for (int m = 2; m < 16; m++) {
				int start = m * 2, end = N;
				while (start <= end) {
					int mid = start + end >> 1;
					if (C(mid, m) == N) {
						ans = min(ans, (mid + 1L) * mid / 2 + m + 1);
						break;
					}
					if (C(mid, m) > N)
						end = mid - 1;
					else
						start = mid + 1;
				}
			}
			System.out.println(ans);
		}
	}

	long min(long a, long b) {
		return a < b ? a : b;
	}

	long C(int n, int m) {
		long num = 1;
		for (int nm = 1; nm <= m; n--, nm++)
			if ((num = num * n / nm) > N)
				return num;
		return num;
	}
}

9, Question I: bidirectional sorting

Time limit: 5.0s memory limit: 512.0MB total score of this question: 25 points

[problem description]

Given sequence (a1, a2, ····, an) = (1, 2, ···, n), i.e. ai = i.

Xiaolan will perform m operations on this sequence. Each time, it may arrange a1, a2, ···, aqi in descending order or aqi, aqi + 1, ···, an in ascending order.

Request the sequence after the operation is completed.

[input format]

The first line of input contains two integers n and m, which respectively represent the length of the sequence and the number of operations.

Next, line m describes the operation on the sequence, where line i contains two integers PI, and Qi represents the operation type and parameters. When pi = 0, it means that a1, a2, ····, aqi are arranged in descending order; When pi = 1, it means aqi, aqi + 1, ····, an are arranged in ascending order.

[output format] output a line containing n integers. Adjacent integers are separated by a space to represent the sequence after the operation is completed.

[sample input]

3 3

0 3

1 2

0 2

[sample output] 3 1 2

[example description]

The original sequence is (1, 2, 3).

After step 1 is (3, 2, 1).

After step 2 is (3, 1, 2).

After step 3 is (3, 1, 2). The same as after step 2, because the first two numbers are in descending order.

[evaluation case scale and agreement]

For 30% of the evaluation cases, n, m ≤ 1000;

For 60% of the evaluation cases, n, m ≤ 5000;

For all evaluation cases, 1 ≤ n, m ≤ 100000, 0 ≤ ai ≤ 1, 1 ≤ bi ≤ n.

Solution 1: eliminate redundancy

[analysis]: violent CMP

The first game of the 12th Blue Bridge Cup 2021 provincial competition (group B of Java University)

package provincialGames_12_2021_1_JavaB;

import java.io.*;
import java.util.*;

public class I09_Bidirectional sorting {
	public static void main(String[] args) {
		new I09_Bidirectional sorting().run();
	}

	void run() {
		InputReader in = new InputReader(System.in);
		PrintWriter out = new PrintWriter(System.out);
		int n = in.readInt(), m = in.readInt();
		Deque<Step> deque = new ArrayDeque();
		deque.push(new Step(1, 1));
		while (m-- > 0) {
			int p = in.readInt();
			int q = in.readInt();
			while (deque.size() > 0 && deque.peek().p == p)
				if (p == 0)
					q = max(q, deque.pop().q);
				else
					q = min(q, deque.pop().q);
			deque.push(new Step(p, q));
		}
		Integer[] ans = new Integer[n];
		for (int i = 0; i < n; i++)
			ans[i] = i + 1;
		deque.pollLast();
		while (deque.size() > 0) {
			Step step = deque.pollLast();
			if (step.p == 0)
				Arrays.sort(ans, 0, step.q, (a, b) -> (b - a));
			else
				Arrays.sort(ans, step.q - 1, n);
		}
		for (int i = 0; i < n; i++) {
			out.print(ans[i]);
			out.print(' ');
		}
		out.flush();
	}

	int max(int a, int b) {
		return a > b ? a : b;
	}

	int min(int a, int b) {
		return a < b ? a : b;
	}

	class Step {
		int p, q;

		Step(int p, int q) {
			this.p = p;
			this.q = q;
		}
	}

	class InputReader {
		BufferedReader reader;
		StringTokenizer token;

		InputReader(InputStream in) {
			this.reader = new BufferedReader(new InputStreamReader(in));
		}

		String read() {
			while (token == null || !token.hasMoreTokens()) {
				try {
					token = new StringTokenizer(reader.readLine());
				} catch (IOException e) {
					e.printStackTrace();
				}
			}
			return token.nextToken();
		}

		int readInt() {
			return Integer.parseInt(read());
		}
	}
}

Solution 2: number filling game

package provincialGames_12_2021_1_JavaB;

import java.io.*;
import java.util.*;

public class I09_Bidirectional sorting 2 {
	public static void main(String[] args) {
		new I09_Bidirectional sorting 2().run();
	}

	void run() {
		InputReader in = new InputReader(System.in);
		PrintWriter out = new PrintWriter(System.out);
		int n = in.readInt(), m = in.readInt(), top;
		Step[] stack = new Step[m + 1];
		for (top = 0; m-- > 0;) {
			int p = in.readInt();
			int q = in.readInt();
			if (p == 0) {
				while (top > 0 && stack[top].p == p)
					q = max(q, stack[top--].q);
				while (top > 1 && stack[top - 1].q <= q)
					top -= 2;
				stack[++top] = new Step(p, q);
			} else if (top > 0) {
				while (top > 0 && stack[top].p == p)
					q = min(q, stack[top--].q);
				while (top > 1 && stack[top - 1].q >= q)
					top -= 2;
				stack[++top] = new Step(p, q);
			}
		}
		int[] ans = new int[n + 1];
		int a = n, l = 0, r = n - 1;
		for (int i = 1; i <= top; i++)
			if (stack[i].p == 0)
				while (r >= stack[i].q && l <= r)
					ans[r--] = a--;
			else
				while (l + 1 < stack[i].q && l <= r)
					ans[l++] = a--;
		if ((top & 1) == 1)
			while (l <= r)
				ans[l++] = a--;
		else
			while (l <= r)
				ans[r--] = a--;
		for (int i = 0; i < n; i++) {
			out.print(ans[i]);
			out.print(' ');
		}
		out.flush();
	}

	int max(int a, int b) {
		return a > b ? a : b;
	}

	int min(int a, int b) {
		return a < b ? a : b;
	}

	class Step {
		int p, q;

		Step(int p, int q) {
			this.p = p;
			this.q = q;
		}
	}

	class InputReader {
		BufferedReader reader;
		StringTokenizer token;

		InputReader(InputStream in) {
			this.reader = new BufferedReader(new InputStreamReader(in));
		}

		String read() {
			while (token == null || !token.hasMoreTokens()) {
				try {
					token = new StringTokenizer(reader.readLine());
				} catch (IOException e) {
					e.printStackTrace();
				}
			}
			return token.nextToken();
		}

		int readInt() {
			return Integer.parseInt(read());
		}
	}
}

Solution 3: chthally tree

package provincialGames_12_2021_1_JavaB;

import java.io.*;
import java.util.*;

public class I09_Bidirectional sorting 3 {
	public static void main(String[] args) {
		new I09_Bidirectional sorting 3().run();
	}

	void run() {
		InputReader in = new InputReader(System.in);
		int n = in.readInt(), m = in.readInt();
		Node[] root = new Node[n + 1];
		int[] P = new int[n + 1];
		Range lower, temp, now;
		lower = now = new Range(0);
		for (int i = 1; i <= n; i++) {
			now = now.next = new Range(i);
			root[i] = build(1, n, i);
		}
		now.next = new Range(n + 1);
		while (m-- > 0) {
			int p = in.readInt();
			int L = in.readInt();
			int R = n;
			if (p == 0) {
				R = L;
				L = 1;
			}
			now = lower;
			while (now.next.L <= L)
				now = now.next;
			if (L > now.L) {
				root[L] = split(root[now.L], L - now.L, P[now.L]);
				now = now.next = new Range(L, now.next);
			}
			temp = now;
			Node pq = null;
			while (now.L <= R) {
				if (now.next.L > R + 1)
					root[R + 1] = split(root[now.L], R + 1 - now.L, P[R + 1] = P[now.L]);
				pq = merge(pq, root[now.L]);
				now = now.next;
			}
			if (now.L == R + 1)
				temp.next = now;
			else
				temp.next = new Range(R + 1, now);
			root[L] = pq;
			P[L] = p;
		}
		StringBuilder ans = new StringBuilder();
		while ((lower = lower.next).L <= n)
			buildAns(ans, root[lower.L], 1, n, P[lower.L]);
		System.out.println(ans);
	}

	Node split(Node tree, int k, int p) {
		if (tree == null)
			return null;
		Node split = new Node(0);
		if (p == 0) {
			int K = K(tree.right);
			if (k <= K) {
				if (k != K)
					split.right = split(tree.right, k, p);
				split.left = tree.left;
				tree.left = null;
			} else
				split.left = split(tree.left, k - K, p);
		} else {
			int K = K(tree.left);
			if (k <= K) {
				if (k != K)
					split.left = split(tree.left, k, p);
				split.right = tree.right;
				tree.right = null;
			} else
				split.right = split(tree.right, k - K, p);
		}
		split.k = tree.k - k;
		tree.k = k;
		return split;
	}

	Node merge(Node tree1, Node tree2) {
		if (tree1 == null)
			return tree2;
		if (tree2 != null) {
			tree1.k += K(tree2);
			tree1.left = merge(tree1.left, tree2.left);
			tree1.right = merge(tree1.right, tree2.right);
		}
		return tree1;
	}

	Node build(int L, int R, int k) {
		if (L == R)
			return new Node(1);
		Node node = new Node(1);
		int mid = L + R >> 1;
		if (k <= mid)
			node.left = build(L, mid, k);
		else
			node.right = build(mid + 1, R, k);
		return node;
	}

	void buildAns(StringBuilder builder, Node root, int L, int R, int p) {
		if (root == null)
			return;
		if (L == R)
			builder.append(L).append(' ');
		else {
			int mid = L + R >> 1;
			if (p == 0) {
				buildAns(builder, root.right, mid + 1, R, p);
				buildAns(builder, root.left, L, mid, p);
			} else {
				buildAns(builder, root.left, L, mid, p);
				buildAns(builder, root.right, mid + 1, R, p);
			}
		}
	}

	int K(Node node) {
		return node == null ? 0 : node.k;
	}

	class Range {
		int L;

		Range next;

		Range(int L) {
			this(L, null);
		}

		Range(int L, Range next) {
			this.L = L;
			this.next = next;
		}
	}

	class Node {
		int k = 1;

		Node left, right;

		Node(int k) {
			this.k = k;
		}
	}

	class InputReader {
		BufferedReader reader;
		StringTokenizer token;

		InputReader(InputStream in) {
			this.reader = new BufferedReader(new InputStreamReader(in));
		}

		String read() {
			while (token == null || !token.hasMoreTokens()) {
				try {
					token = new StringTokenizer(reader.readLine());
				} catch (IOException e) {
					e.printStackTrace();
				}
			}
			return token.nextToken();
		}

		int readInt() {
			return Integer.parseInt(this.read());
		}
	}
}

10, Question J: parenthesis sequence

Time limit: 5.0s memory limit: 512.0MB total score of this question: 25 points

[problem description]

Given a bracket sequence, it is required to add as few brackets as possible to make the bracket sequence legal. When the addition is completed, different addition results will be produced. How many essentially different addition results are there. The two results are essentially different, which means that there is a certain position. One result is the left parenthesis and the other is the right parenthesis.

For example, for the bracket sequence ((()), you only need to add two brackets to make it legal. There are several different adding results: () () (), () () () (), () (), and (()).

[input format] the input line contains a string s, which indicates the given sequence of parentheses. There are only left and right parentheses in the sequence.

[output format] output an integer to represent the answer. The answer may be large. Please output the remainder of the answer divided by 100000007 (i.e. 10 ^ 9 + 7).

[sample input] ()

[sample output] 5

[evaluation case scale and agreement]

For 40% of the evaluation cases, | s | ≤ 200.

For all evaluation cases, 1 ≤| s | ≤ 5000.

Solution I

[analysis]: simulate the process according to the topic.

package provincialGames_12_2021_1_JavaB;

import java.util.Scanner;

public class J10_Bracket sequence {
	public static void main(String[] args) {
		new J10_Bracket sequence().run();
	}

	int mod = 1000000007;

	void run() {
		byte[] line = new byte[5555];
		try {
			int n = System.in.read(line, 1, 5050) - 1;
			System.out.println(calc(line, n, false) * calc(line, n, true) % mod);
		} catch (java.io.IOException e) {
			e.fillInStackTrace();
		}
	}

	long calc(byte[] str, int n, boolean turn) {
		if (turn)
			reverse(str, n);
		int[][] dp = new int[n + 1][n + 2];
		int opening = 0;
		dp[0][0] = 1;
		for (int i = 1; i <= n; i++) {
			if (str[i] == '(') {
				for (int j = 1; j <= n; j++)
					dp[i][j] = dp[i - 1][j - 1];
				opening++;
			} else {
				dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
				for (int j = 1; j <= n; j++)
					dp[i][j] = (dp[i][j - 1] + dp[i - 1][j + 1]) % mod;
				if (opening > 0)
					opening--;
			}
		}
		return dp[n][opening];
	}

	void reverse(byte[] arr, int n) {
		for (int i = 1, j = n; i <= j; i++, j--) {
			byte temp = (byte) (arr[i] ^ 1);
			arr[i] = (byte) (arr[j] ^ 1);
			arr[j] = temp;
		}
	}
}

Summary

Look at other people's notes.

Topics: Java Algorithm data structure

Programmer Think

Detailed explanation and summary of the real topic of the 12th Blue Bridge Cup Java group B provincial competition in 2021 [the first provincial competition 2021.04.18]

1, Question A: ASC

Solution 1: ASCII calculation

Solution 2: Call of class

2, Question B: card

Solution 1: Enumeration

Solution 2: simple solution

Solution 3: overtaking in curve

3, Question C: straight line

Solution 1: set of linear equations

Solution 2: fraction elimination error

Solution 3: plane geometry

4, Question D: goods placement

Solution 1: violent search

Solution 2: scaling quality factor

5, Question E: Path

Solution 1: Search

Solution 2: Search - branch cutting and wide search

Solution 3: single source shortest path Dijkstra

Solution 4: single source shortest path Floyd

6, Question F: time display

Solution 1: simulation calculation

Solution 2: direct calculation

Solution 3: Java date API

7, Question G: minimum weight

Solution 1: ternary

Solution 2: variant ternary

8, Question H: Yang Hui triangle

Solution 1: analogy monotone sequence

9, Question I: bidirectional sorting

Solution 1: eliminate redundancy

Solution 2: number filling game

Solution 3: chthally tree

10, Question J: parenthesis sequence

Solution I

Summary

Hot Topics