Find the median of two positively ordered arrays

Method 1: binary search

Given two ordered arrays, it is required to find the median of two ordered arrays. The most intuitive ideas are as follows:

• Using the merging method, merge two ordered arrays to get a large ordered array. The element in the middle of a large ordered array is the median.
• There is no need to merge two ordered arrays, just find the position of the median. Since the length of the two arrays is known, the sum of the subscripts of the two arrays corresponding to the median is also known. Maintain two pointers. Initially, point to the position of subscript 00 of the two arrays respectively. Move the pointer pointing to the smaller value one bit at a time (if one pointer has reached the end of the array, you only need to move the pointer of the other array) until it reaches the median position.

Assuming that the lengths of two ordered arrays are m and n respectively, what is the complexity of the above two ideas?

The time complexity of the first idea is O(m+n), and the space complexity is O(m+n). The second idea can reduce the spatial complexity to O(1), but the time complexity is still O(m+n).

How to reduce the time complexity to O(log(m+n))? If there are log requirements for time complexity, binary search is usually required. This problem can also be realized through binary search.

According to the definition of median, when m+n is odd, the median is the (m+n) / 2nd element in two ordered arrays. When m+n is even, the median is the average of (m+n) / 2nd element and (m+n) / 2nd + 1st element in two ordered arrays. Therefore, this problem can be transformed into finding the smallest number k in two ordered arrays, where k is (m+n)/2 or (m+n)/2+1.

Suppose two ordered arrays are A and B, respectively. To find the k-th element, we can compare A[k/2 − 1] with B[k/2 − 1], where / represents integer division. Since A[0... k/2 − 2] and B[0... k/2 − 2] are respectively preceded by A[k/2 − 1] and B[0... k/2 − 2], that is, k/2 − 1 elements, for the smaller value in A[k/2 − 1] and B[k/2 − 1], at most (k/2 − 1)+(k/2 − 1) ≤ K − 2 elements are smaller than it, then it cannot be the smallest number K.

Therefore, we can sum up three situations:

[the external chain image transfer fails, and the source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-Gtgme9LQ-1624102558528)(C:\Users\cai'yo \ appdata \ roaming \ typora user images \ image-20210617212705835. PNG)]

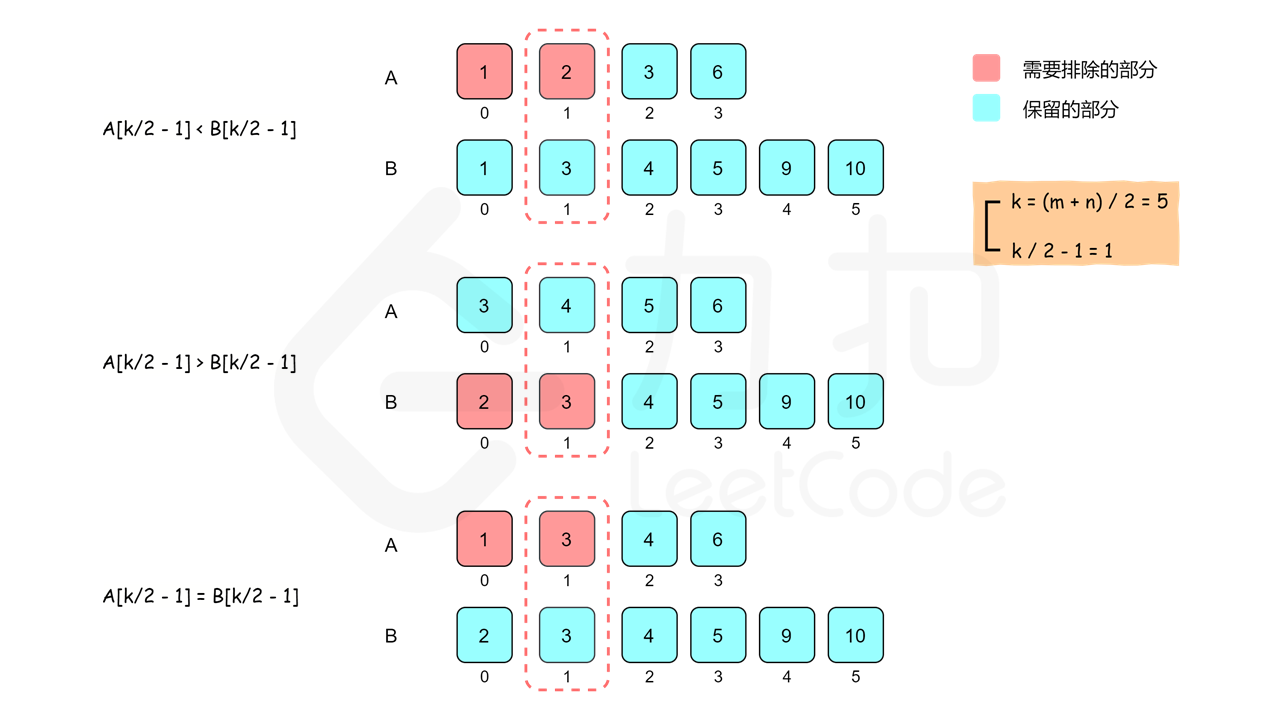
It can be seen that after comparing A[k/2 − 1] and B[k/2 − 1], k/2 can not be the smallest number k, and the search range is reduced by half. At the same time, we will continue the binary search on the excluded new array, and reduce the value of K according to the number of excluded numbers, because the number of excluded numbers is not greater than the smallest number of K. There are three situations that need special treatment:

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-BIHk7WhQ-1624102558535)(C:\Users\cai'yo \ appdata \ roaming \ typora user images \ image-20210617212805132. PNG)]

An example is given to illustrate the above algorithm. Suppose two ordered arrays are as follows:

A: 1 3 4 9
B: 1 2 3 4 5 6 7 8 9

The lengths of the two ordered arrays are 4 and 9 respectively, the sum of the lengths is 13, and the median is the seventh element in the two ordered arrays. Therefore, you need to find the k = 7th element.

Compare the numbers with subscript k/2 − 1 = 2 in two ordered arrays, i.e. A[2] and B[2], as shown below:

A: 1 3 4 9
       ↑
B: 1 2 3 4 5 6 7 8 9
       ↑

Since a [2] > B[2], B[0] to B[2] are excluded, that is, the subscript offset of array B becomes 3, and the value of K is updated: k=k − k/2=4.

Next, find and compare the numbers with subscript k/2 − 1 = 1 in two ordered arrays, i.e. A[1] and B[4], as shown below, where the square brackets represent the excluded numbers.

A: 1 3 4 9
     ↑
B: [1 2 3] 4 5 6 7 8 9
             ↑

Since A[1] < B [4], exclude A[0] to A[1], that is, the subscript offset of array A becomes 2, and update the value of K: k=k − k/2=2.

Next, find and compare the numbers with subscript k/2 − 1 = 0 in two ordered arrays, that is, compare A[2] and B[3], as shown below, where the square brackets represent the excluded numbers.

A: [1 3] 4 9
         ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

Since A[2]=B[3], according to the previous rule, the elements in A are excluded, so A[2] is excluded, that is, the subscript offset of array A becomes 3, and the value of K is updated: k=k − k/2=1.

Since the value of k becomes 1, compare the first number in the range of non excluded subscripts in the two ordered arrays, and the smaller number is the k number. Since a [3] > b [3], the k number is B[3]=4.

A: [1 3 4] 9
           ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            double median = getKthElement(nums1, nums2, midIndex + 1);
            return median;
        } else {
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
            return median;
        }
    }

    public int getKthElement(int[] nums1, int[] nums2, int k) {
        /* Main idea: to find the element with the smallest K (k > 1), take pivot 1 = nums1 [K / 2-1] and pivot 2 = nums2 [K / 2-1] for comparison
         * "/" here means division
         * nums1 There are nums1 [0.. K / 2-2] elements smaller than or equal to pivot 1, with a total of k/2-1
         * nums2 There are nums2 [0.. K / 2-2] elements smaller than or equal to pivot 2, with a total of k/2-1
         * Take pivot = min (pivot 1, pivot 2), and the total number of elements less than or equal to pivot in the two arrays will not exceed (K / 2-1) + (K / 2-1) < = K-2
         * In this way, pivot itself can only be the k-1 smallest element
         * If pivot = pivot 1, nums1 [0.. K / 2-1] cannot be the k-th smallest element. All these elements are "deleted", and the rest are used as a new nums1 array
         * If pivot = pivot 2, nums2 [0.. K / 2-1] cannot be the k-th smallest element. All these elements are "deleted", and the rest are used as a new nums2 array
         * Because we "deleted" some elements (these elements are smaller than the element smaller than k), we need to modify the value of K and subtract the number of deleted elements
         */

        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {
            // Boundary condition
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }
            
            // Normal condition
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

Complexity analysis

• Time complexity: O(log(m+n)), where m and N are the lengths of arrays nums1 and nums2 respectively. Initially, there is k=(m+n)/2 or k=(m+n)/2+1. Each cycle can reduce the search range by half, so the time complexity is O(log(m+n)).
• Space complexity: O(1).