preface
We all know that there are five commonly used classical algorithms: divide and conquer algorithm, greedy algorithm, dynamic programming algorithm, backtracking algorithm, branch and bound algorithm. Each algorithm plays a very important role in computer science; This article will introduce an implementation of the divide and conquer algorithm, including sequential search, binary search, quick sort, merge sort and so on
definition
Divide and conquer literally means that a complex problem is divided into two or more identical or similar subproblems, and the subproblem is divided into smaller problems.... Until the end, the sub problem can be solved simply, that is, the answer to the sub problem is the answer to the original problem. If you look at it like this, do you think it's not important to suddenly think of an algorithm? Yes, it's recursion, or maybe you think of a merge sorting algorithm or a binary search method. This idea is the basis of these algorithms. Then let's understand this algorithm from a young age and a big age
Sequential search
If the linear table is an unordered table, that is, the arrangement of elements in the table is unordered, sequential search must be used regardless of whether the linear table adopts sequential storage or chain storage. If the linear table is ordered, the chain storage structure is adopted, and the sequential search method must also be used
- This method is the most commonly used search method in our code development;
- For example, find a value in the LinkedList (linked list structure). Of course, this method is adopted in the tree structure.
- The following figure is an embodiment of sequential search in binary sort tree
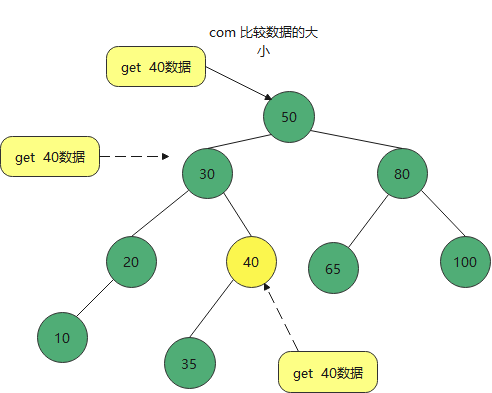
Binary search method
Prerequisite: the binary search method can be performed only after the data has been sorted. The {array sequential storage structure
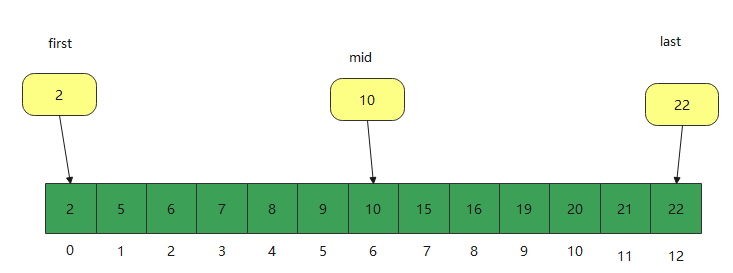
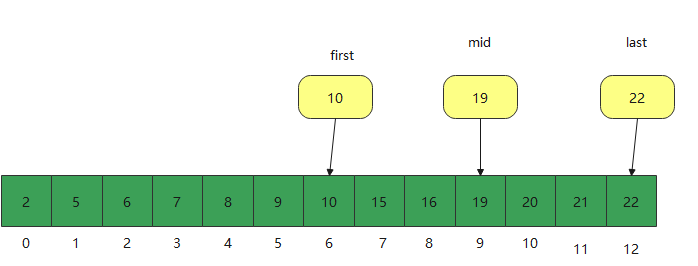
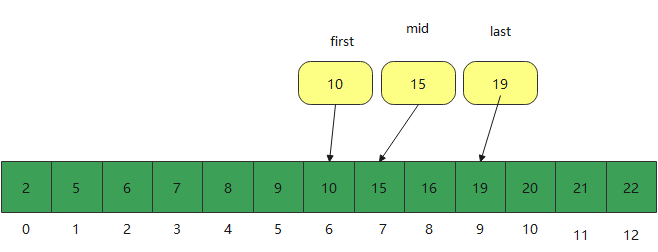
Through the analysis of the above figure, we can see that the search rate of our binary search method is quite fast. We can find the method in the sequential array, and the time complexity is only O(logn), that is, if you have 8 elements, you can find them only three times; This is also to split the problem and minimize the problem.
It is difficult to write a binary search correctly. It needs to be designed into a left closed right open structure, which is an idea of no repetition in the interval; A large number of mathematical functions such as random(0, 1) are used in for (int, I = 0; I < array. Length; I + +)
We decompose it from a piece of code
/**
* Binary search
*/
public static int binarySearch(int[] array,int fromIndex,int toIndex,int key){
int low=fromIndex;
int high=toIndex-1;
while(low<=high){
int mid=(low+high)/2;//Take the middle
int midVal=array[mid];
if(key>midVal){//Go to the right
low=mid+1;
}else if(key<midVal){//Go to the left
high=mid-1;
}else{
return mid;
}
}
return -(low+1);//low+1 means that it stops at the low+1 element when it cannot be found
}- First, toIndex -1 is to open the left and close the right section
- Judge whether it is over, and judge that low is greater than high pointer
- Get intermediate pointer int mid=(low+high)/2
- int midVal=array[mid] get the data of the intermediate pointer
- The judgment value is greater than mid, low=mid+1; Assignment
- In this way, the data can be quickly found through continuous circulation
This analysis feels that the binary search method is very simple, but we need to pay attention to the interval between left and right; And jump out of the condition of the loop
Quick sort (pre sort)
Quick sort because the sorting efficiency is higher in several sorting methods with the same name of O(N*logN), and the idea of quick sort - divide and conquer method is indeed practical, let's analyze quick sort
principle
The main point is that all the data of one part is smaller than that of the other part, and then quickly sort the two parts of data according to the secondary method. The whole sorting process can be recursive or non recursive, so as to turn the whole data into an ordered sequence.
A quick sort process
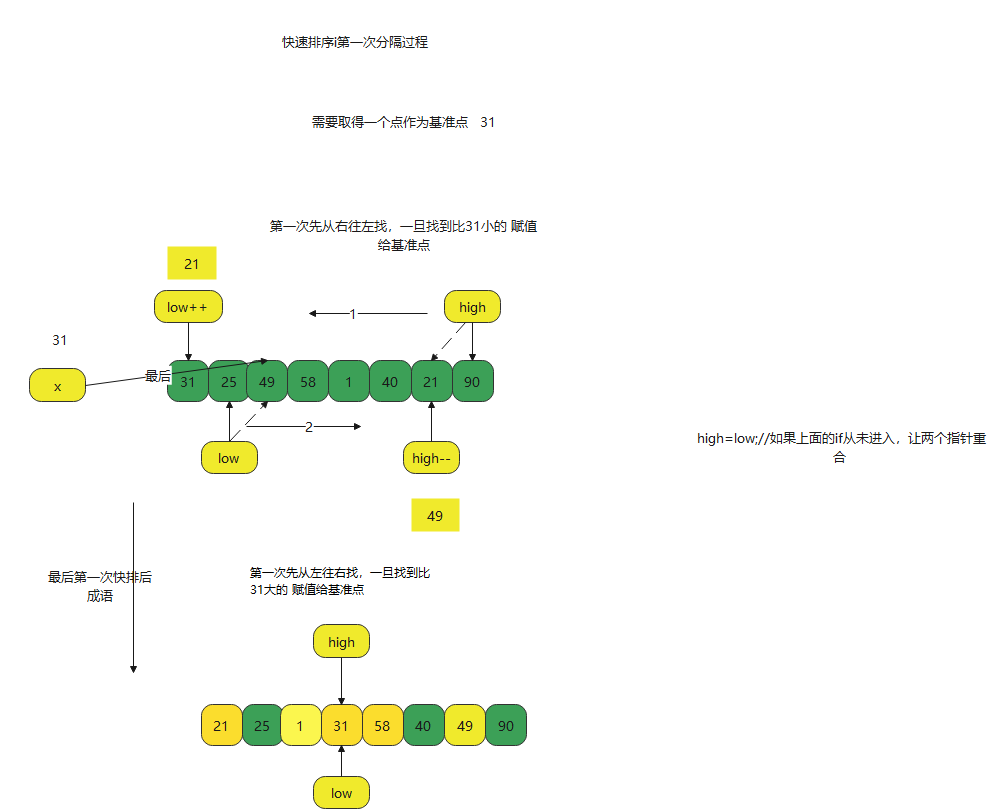
Code analysis is a fast sorting process
public static void quickSort(int[] array,int begin,int end){
if(end-begin<=0) return;
int x=array[begin];
int low=begin;//0
int high=end;//5
//Since the data will be taken from both ends, one direction is required
boolean direction=true;
L1:
while(low<high){
if(direction){//Look right to left
for(int i=high;i>low;i--){
if(array[i]<=x){
array[low++]=array[i];
high=i;
direction=!direction;
continue L1;
}
}
high=low;//If the above if never enters, make the two pointers coincide
}else{
for(int i=low;i<high;i++){
if(array[i]>=x){
array[high--]=array[i];
low=i;
direction=!direction;
continue L1;
}
}
low=high;
}
}
//Put the last found value in the middle
array[low]=x;
//Start to complete the left and right operations
quickSort(array,begin,low-1);
quickSort(array,low+1,end);
}- First, obtain the datum point of # comparison, and obtain the start point and end point
if(end-begin<=0) return;
int x=array[begin];
int low=begin;//0
int high=end;//5- Secondly, you need to record a direction, because when sorting quickly, you need to move the sorting method from left to right
//Since the data will be taken from both ends, one direction is required
boolean direction=true;- Go from right to left. As long as you find something smaller than the reference point, you can exchange the value of the basic point and exchange the direction
if(direction){//Look right to left
for(int i=high;i>low;i--){
if(array[i]<=x){
array[low++]=array[i];
high=i;
direction=!direction;
continue L1;
}
}
high=low;//If the above if never enters, make the two pointers coincide
}- Go from left to left, as long as you find something smaller than the reference point, exchange the value of the basic point and exchange the direction
else{
for(int i=low;i<high;i++){
if(array[i]>=x){
array[high--]=array[i];
low=i;
direction=!direction;
continue L1;
}
}
low=high;
}- When low is equal to high, jump to the cycle for one time, and the fast platoon ends {while (low < high)
- Put the last found value into the value of the reference in the middle position
array[low]=x;
- Start to complete the left and right operations
quickSort(array,begin,low-1);
quickSort(array,low+1,end);This is the basic idea and implementation of the whole fast scheduling. The data is sorted in sections, but there is a certain application scenario. The amount of data is large and the structure is linear;
Weaknesses
When there is a large amount of duplicate data, the performance is not good
The processing performance of one-way chain structure is poor (generally speaking, the chain structure is not used)
Therefore, we use another algorithm, which is also the embodiment of divide and conquer, to sort (merge sort (post order))
Merge sort (post order)
The idea of merging and sorting and the idea of fast sorting are both from divide and conquer, so the idea is very similar. When we want to sort an array, we first split the array into two halves, find a way to sort the two sub arrays, and then merge the two ordered sub arrays into an ordered array. The difference between this and fast scheduling is that fast scheduling is based on the operation on the original array, while merging requires splitting multiple arrays
principle
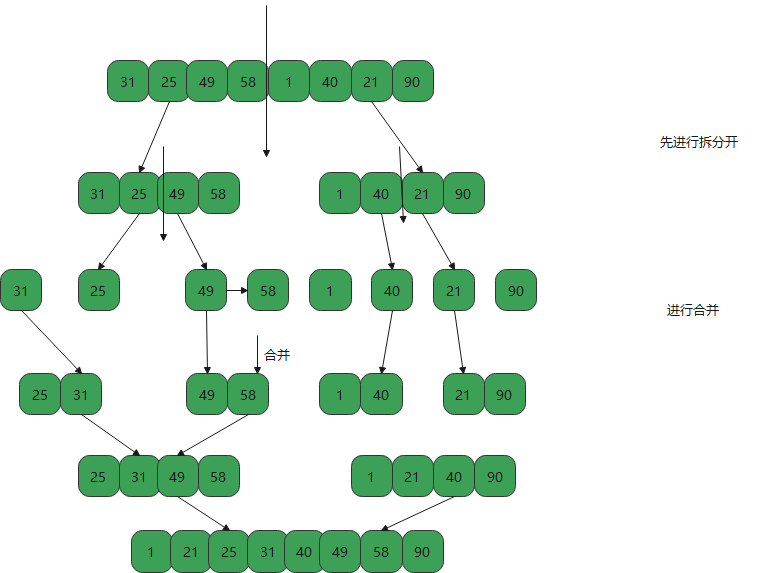
Implementation mode
//Merge sort
public static void mergeSort(int array[],int left,int right){
if(left==right){
return;
}else{
int mid=(left+right)/2;
mergeSort(array,left,mid);
mergeSort(array,mid+1,right);
merge(array,left,mid+1,right);
}
}
// 0 4 7
// 1 2 5 9 === 3 4 10 11
public static void merge(int[] array,int left,int mid,int right){
int leftSize=mid-left;
int rightSize=right-mid+1;
//Generate array
int[] leftArray=new int[leftSize];
int[] rightArray=new int[rightSize];
//Fill data
for(int i=left;i<mid;i++){
leftArray[i-left]=array[i];
}
for(int i=mid;i<=right;i++){
rightArray[i-mid]=array[i];
}
//merge
int i=0;
int j=0;
int k=left;
while(i<leftSize && j<rightSize){
if(leftArray[i]<rightArray[j]){
array[k]=leftArray[i];
k++;i++;
}else{
array[k]=rightArray[j];
k++;j++;
}
}
while(i<leftSize){
array[k]=leftArray[i];
k++;i++;
}
while(j<rightSize){
array[k]=rightArray[j];
k++;j++;
}
}- Let's start with splitting, using the feature of recursion to split left and right continuously
public static void mergeSort(int array[],int left,int right){
if(left==right){
return;
}else{
int mid=(left+right)/2;
mergeSort(array,left,mid);
mergeSort(array,mid+1,right);
merge(array,left,mid+1,right);
}
}- merge generates a new array from the split data and fills it with data
int leftSize=mid-left;
int rightSize=right-mid+1;
//Generate array
int[] leftArray=new int[leftSize];
int[] rightArray=new int[rightSize];
//Fill data
for(int i=left;i<mid;i++){
leftArray[i-left]=array[i];
}
for(int i=mid;i<=right;i++){
rightArray[i-mid]=array[i];
}- Merge data
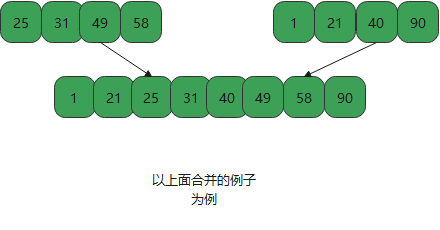
- Merge and sort left and right codes
//merge
int i=0;
int j=0;
int k=left;
while(i<leftSize && j<rightSize){
if(leftArray[i]<rightArray[j]){
array[k]=leftArray[i];
k++;i++;
}else{
array[k]=rightArray[j];
k++;j++;
}
}When leftarray [i] > rightarray [J]
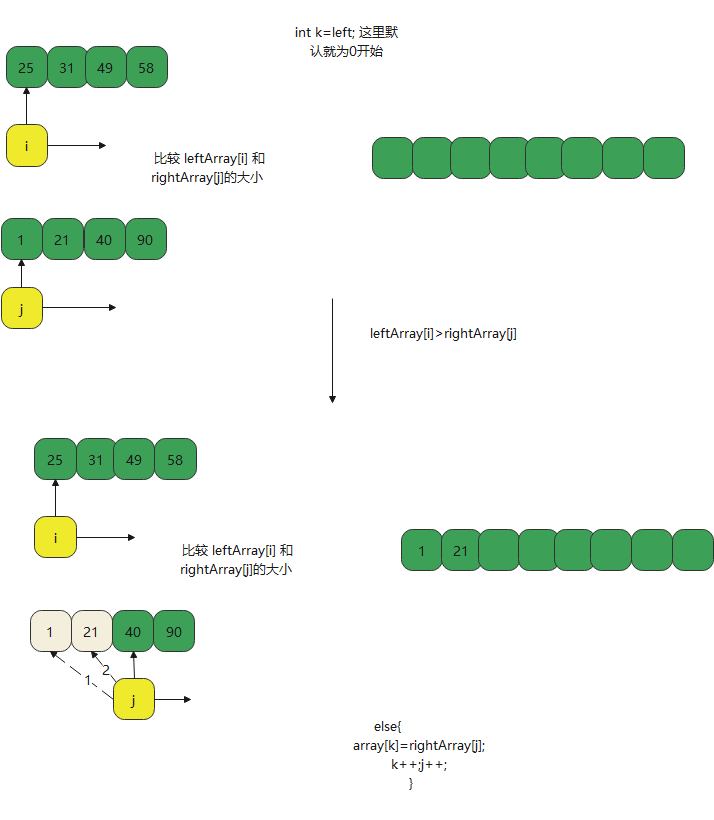
When leftarray [i] < rightarray [J]
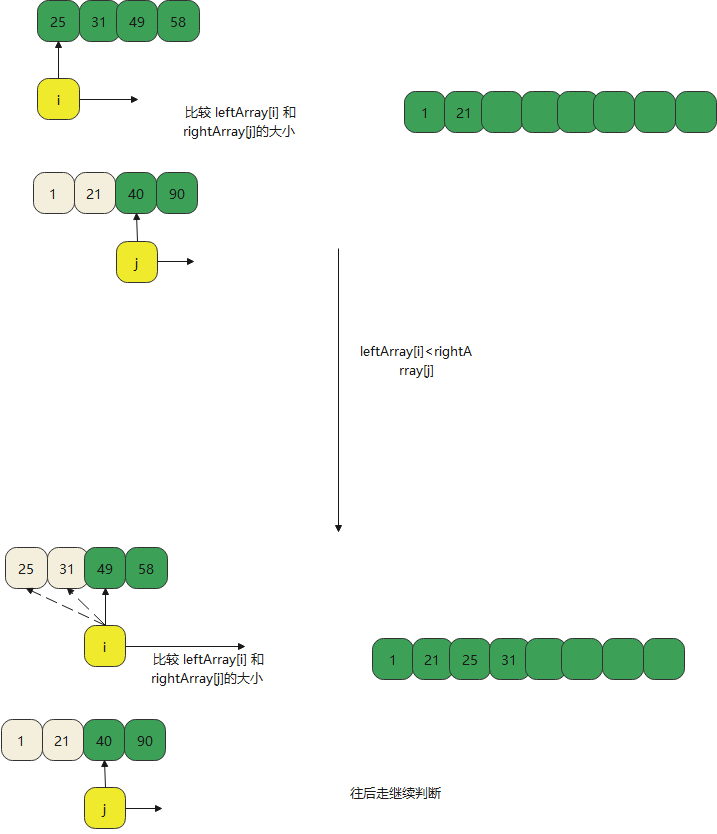
This minimizes merge sorting
- Finally, reference minimization is needed for filling
while(i<leftSize){
array[k]=leftArray[i];
k++;i++;
}
while(j<rightSize){
array[k]=rightArray[j];
k++;j++;
}Such a complete merging and sorting is completed
- Application scenario of merging and sorting
Large amount of data and a lot of duplicate data, chain structure
- Weaknesses
Large space required
summary
The application of the whole divide and conquer method accounts for a large part of the whole algorithm. Here, binary search method, fast sorting and merging sorting are all the applications of divide and conquer method, but in real programming, they are not limited to this.