catalogue
Afternoon: divide and conquer algorithm (1)
Basic application of divide and conquer thought:
Quick sort in divide and Conquer:
Examples of pictures and words:
Merge sort in divide and Conquer:
The difference between merging and fast scheduling:
Day 1
9:00 - 11:00 am, bottom test
T1: bouncing grasshopper
Time limit: 1000ms; space limit: 256MB
Input file: jump In output file: jump out
Title Description
Now, there is a grasshopper at x0 on a number axis.
Because it had nothing to do, it had an idea and began to bounce training on the number axis. Because the grasshopper likes positive integers very much, it will jump forward by 1 unit in the first minute, 2 units in the second minute, and so on. The grasshopper thinks it's meaningless to jump straight ahead. Therefore, it stipulates that if it is in an even number of point coordinates before this jump, it will jump to the left, otherwise it will jump to the right.
For example, if the grasshopper reaches coordinate point 7 after 18 consecutive jumps, when it makes the 19th jump, because its current position is odd, it will jump 19 units to the right and reach coordinate point 19 + 7 = 26. When it makes the 20th jump, because the current coordinate point 26 is even, it will jump 20 unit lengths to the left to reach the coordinate point 26-20 = 6
Now, given the size of the grasshopper's initial coordinate point, please find out the position that the grasshopper will reach after jumping times.
Input format
In the first line, enter a number T (1 ≤ t ≤ 1e4) to indicate the number of tests of the sample.
In the next line, there are two numbers in each line. The first number x0(-1e14 ≤ x0 ≤ 1e14) represents the initial position of the grasshopper, and the second number n(1 ≤ t ≤ 1e14) represents the number of jumps.
Output format
For each problem, the coordinate point position reached after n jumps is output.
sample input
9
0 1
0 2
10 10
10 99
177 13
10000000000 987654321
-433494437 87178291199
1 0
-1 1
Output sample
-1
1
11
110
190
90
12345679
-87611785637
1
0
Example explanation
analysis
For the first question. The grasshopper's initial position is at the coordinate 0. Because 0 is an even number, the grasshopper will jump 1 unit length to the left first, so the answer to the first question is - 1
For the second question, the grasshopper's initial position is at the beginning of coordinate 0, because 0 is an even number. Therefore, for the first time, jump one unit length to the left to reach - 1, because - 1 is an odd number. Therefore, jump two to the right to reach coordinate point 1 for the second time to get the answer.
It is easy for us to simulate according to the meaning of the topic and get the following code:
#include <bits/stdc++.h>
using namespace std;
int T;
long long x, n;
int main() {
scanf("%d", &T);
while(T--) {
scanf("%lld%lld", &x, &n);
for (int i = 1;i <= n;i++) {
if (x & 1) {
x += i;
} else {
x -= i;
}
}
printf("%lld\n", x);
}
return 0;
} be careful:
(1) x must define a long long int.
(2) '&' in "X & 1" is a bit operation, which is used to judge whether x can be divided by 2.
Well, Congratulations, TLE, 0.
So, how to optimize it?
Find rules!
By the way, how to find rules faster, more accurate and more advanced.
First, you need a violence program and a data generator.
As follows:
Violent procedures:
#include <bits/stdc++.h>
using namespace std;
int T;
long long x, n;
int main() {
freopen("1.in", "r", stdin);
freopen("1.out", "w", stdout);
scanf("%d", &T);
while(T--) {
scanf("%lld%lld", &x, &n);
for (int i = 1;i <= n;i++) {
if (x & 1) {
x += i;
} else {
x -= i;
}
}
printf("%lld\n", x);
}
return 0;
} Obviously, we should start with odd starting point and even starting point.
Data generator:
1. Even number:
#include <bits/stdc++.h>
using namespace std;
int main() {
freopen("1.in", "w", stdout);
int T = 20;
cout << 20 << endl;
while(T--) {
cout << 0 << " " << 20 - T << endl;
}
return 0;
}Therefore, input data:
20 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 10 0 11 0 12 0 13 0 14 0 15 0 16 0 17 0 18 0 19 0 20
Output data:
-1 1 4 0 -5 1 8 0 -9 1 12 0 -13 1 16 0 -17 1 20 0
2. Odd number:
#include <bits/stdc++.h>
using namespace std;
int main() {
freopen("1.in", "w", stdout);
int T = 20;
cout << 20 << endl;
while(T--) {
cout << 1 << " " << 20 - T << endl;
}
return 0;
}Therefore, input data:
20 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 1 11 1 12 1 13 1 14 1 15 1 16 1 17 1 18 1 19 1 20
Output data:
2 0 -3 1 6 0 -7 1 10 0 -11 1 14 0 -15 1 18 0 -19 1
It's not. The rules come out.
#include <bits/stdc++.h>
using namespace std;
long long T, x, n, xx;
int main() {
//freopen("jump.in", "r", stdin);
//freopen("jump.out", "w", stdout);
scanf("%lld", &T);
while(T--) {
scanf("%lld%lld", &x, &n);
long long xxx = abs(x);
if (xxx % 2 == 1) {
//cout << "B";
if (n % 4 == 1) {
xx = n;
} else if (n % 4 == 2) {
xx = -1;
} else if (n % 4 == 3) {
xx = -1 * n - 1;
} else {
xx = 0;
}
} else {
if (n % 4 == 1) {
xx = -1 * n;
} else if (n % 4 == 2) {
xx = 1;
} else if (n % 4 == 3) {
xx = n + 1;
} else {
xx = 0;
}
}
//cout << x << " " << xx << endl;
printf("%lld\n", x + xx);
}
return 0;
} AC!47ms
T2: Captain Flint's drifting
Memory limit: 256 MiB time limit: 2000 ms
Title Description
Captain Flint and his crew have been drifting in Savage waters in recent months, drinking rum and telling their own stories. At this time, uncle Bogdan would always mention his nephew Dennis and tell him how Dennis helped him solve a difficult problem.
At first, uncle Bogdan wrote down a positive integer on the blackboard, which was composed of numbers. After that, he erased X and changed it to the integer k, which is the number concatenated in binary representation. For example, suppose x=729, then k = 111101001 (because 7 = 111, 2 = 10, 9 = 1001)
However, uncle Bogdan's head is not very smart. He doesn't know how to deal with X. therefore, he asked Dennis to help. Dennis found that he needs to delete the last n numbers of number k, name the new number r, and then find the integer x with length n to maximize R (as a number). If there are more than one X satisfying the condition, choose the smallest one.
At this time, everyone here is full of interest in this problem. Please try to help Uncle Bogdan solve this problem.
Note: in this task, we compare all integers (whether or) as numbers. Therefore, 729 < 1999, 111 < 1000
Input format
Enter a number in the first line to indicate the number of tests
Next, enter a number in each line to indicate the length of the original number and the number of digits to be deleted.
Output format
For each set of tests, one digit is output, indicating that the maximum and minimum digits are met.
Sample
sample input
Copy 2 1 3
sample output
Copy 8 998
Resolution:
If you read the title carefully, you will find that there are only two kinds of numbers, 9 (1001) and 8 (1000), all of which are 4 digits. Why not 7 (111), because there are only 3 digits.
When n=1, 9 and 8 can be selected, and the minimum is selected, then x = 8(1000)
When n=2, both 99 and 98 can be selected. If the minimum is selected, then x = 98(10011000)
When n=3, both 99998 and 99998 can be selected. If the minimum is selected, then x = 998 (10011000)
When n=4, 9999998 can be selected. If the minimum is selected, then x = 9998 (10011000)
When n=5, 9999999999989988 can be selected. If the minimum is selected, then x = 99988 (100110001000)
When n=6, 9999999999999999988 can be selected. If the minimum is selected, then x = 999988 (100110001000)
#include <bits/stdc++.h>
using namespace std;
int T, n, b, c;
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
b = (n + 3) / 4;
c = n - b;
for (int i = 1; i <= c; i++) printf("9");
for (int i = 1; i <= b; i++) printf("8");
puts("");
}
return 0;
}AC!147ms
T3. Tennis match
Memory limit: 256 MiB time limit: 2000 ms
Title Description
Alice and Bob are playing tennis.
In tennis, Alice and Bob will serve in turn, that is, if Alice serves in the first set, Bob serves in the second set, and vice versa.
In a tennis match, if the party who doesn't serve wins the game, then we will call this game a breaking game.
Now, it is known that Alice won the game and Bob won the game, but it is not known who served first and who won the first game.
Now, please calculate and output the number of all possible break points.
Input format
In the first line, enter a number t(1 ≤ t ≤ 1e3) to indicate the number of tests.
In the next line, there are two numbers a and b (0 ≤ a,b ≤ 1e5) in each line, representing the number of games won by Alice and Bob respectively.
Output format
For each set of tests, output two lines respectively.
The first line outputs a number m, indicating the number of possible breaking stations.
The second line outputs a number m, listing the number of breaking stations in all cases.
Sample
sample input
Copy 3 2 1 1 1 0 5
sample output
Copy 4 0 1 2 3 2 0 2 2 2 3
Example explanation
For the first set of samples, there may be
Alice keeps the serve, Bob keeps the serve, Alice keeps the serve, and the number of breaks is 0
Bob keeps the serve, Alice keeps the serve, Alice breaks, the number of breaks is 1
Bob breaks, Alice breaks, Alice keeps the serve, and the number of breaks is 2
Alice breaks, Bob breaks, Alice breaks, the number of breaks is 3
Resolution:
I haven't figured out this question yet. Let's coo it first.
T4 placing sheep
Memory limit: 256 MiB time limit: 1000 ms
Title Description
Now, you are playing a game called placing sheep. The ultimate goal of this game is that you need to arrange all the sheep in a continuous row. In a game level, you will get a string of length. This string consists of the character '.' And the character '*', where '.' Represents a space and '*' represents a sheep. If there is a space in the corresponding position, you can move a sheep one space to the left or right at a time.
For example: if there is a group now, the string is "* *. *." Data, then you can do the following:
First move the sheep in the fourth grid to the right to get "* *.. *."
Move the sheep in the second grid one grid to the right to get "*. *. *."
Then move the sheep in the first grid one grid to the right to get "* *. *"
Move the sheep in the third grid one grid to the right to get "*. * *."
Then move the sheep in the second grid one grid to the right to get ".. * * *."
At this time, all the sheep have lined up in a continuous row, and the game is over.
Now, the topic will tell you the situation of each level. Please calculate how many times you need to move through this level at least?
Input format
In the first line, enter a number to indicate the number of test groups.
For each set of tests, enter a number on the first line to represent the length of the string. On the second line, enter one that contains only '.' And '*'.
The title guarantees that for any test file, the sum will not exceed
Output format
For any game, output the minimum number of moves required for customs clearance.
Sample
sample input
Copy 5 6 **.*.. 5 ***** 3 .*. 3 ... 10 *.*...*.**
sample output
Copy 1 0 0 0 9
In mathematics of grade one of junior high school, there is a theorem of "odd point even segment" (assuming that there is a number axis, and the sum of the distance from the point on the number axis to the middle point (segment) is the smallest)
Then this problem only needs to find the * in the middle of all * and then traverse the calculation;
Because * movement will be limited by other *, the number of * between the target and the end point should be subtracted from the distance;
#include <bits/stdc++.h>
using namespace std;
int T,n, mid, a[1000005];
long long sum;
string s;
int main() {
cin >> T;
while (T--) {
cin >> n;
cin >> s;
int cnt = 0;
for (int i = 0; i < n; i++) {
if (s[i] == '*') a[cnt++] = i;
}
mid = cnt / 2;
for (int i = 0; i < cnt; i++) {
sum += abs(a[mid] - a[i]) - abs(mid - i);
}
cout << sum << endl;
}
return 0;
}Afternoon: divide and conquer algorithm (1)
Concept:
For a problem with scale n: if the problem can be easily solved (for example, the scale n is small), it can be solved directly. Otherwise, it can be decomposed into k smaller subproblems. These subproblems are independent of each other and have the same form as the original problem. These subproblems are solved recursively, and then the solutions of each subproblem are combined to obtain the solution of the original problem. This algorithm design strategy is called divide and conquer.
Features (four "can"):
(1) The scale of the problem can be reduced to a certain extent and can be easily solved (Simplified: solvable).
(2) The problem can be decomposed into several smaller identical problems (Simplified: separable).
(3) The solution of the subproblem decomposed by the problem can be combined into the solution of the problem (simplification: combination).
(4) The subproblems decomposed by the problem are independent of each other, that is, the subproblems do not contain common subproblems (simplification: independence).
Solution steps:
1. Sub: decompose the original problem into several small-scale, independent sub problems with the same form as the original problem.
2. Solution: if the subproblem is small and easy to solve, it can be solved directly, otherwise it can be solved recursively.
3. Combination: combine the solutions of each sub problem into the solutions of the original problem.
Basic application of divide and conquer thought:
Circular competition
Memory limit: 256 MiB time limit: 1000 ms
Title Description
While the king Shura and the evil wolf are on the run, the annual sports meeting of the Academy of magic is in full swing. On the field, Mr. Mo, an amateur commentator, is giving a passionate explanation to the audience: "hyenas... Bite! Bite! The hyenas leader has done meritorious service! Don't give the zebra any chance! Great hyenas! Great hyenas leader! It inherits the glorious history and tradition of beasts! Leopards, tigers and lions have souls at this moment!"
Er, well, let's not worry about the nicknames of the players on the field. The problem now is that there are n players in a certain event to compete in a circular game, where n=2m. Each player is required to compete with other N-1 players once. Each player competes once a day. The round robin lasts for n-1 days. No player is required to take turns every day. The table of competition time is shown in the figure (assuming m=3).
Input format
The input is an integer m, m ≤ 5.
Output format
The output is an integer matrix with n rows and N columns, that is, the competition table. Each element is separated by spaces, and there are no extra spaces at the end of the line. (Note: no file input / output required!)
Sample
sample input
Copy 2
sample output
Copy 1 2 3 4 2 1 4 3 3 4 1 2 4 3 2 1
Resolution:
PS: maybe the data is too small. C2024XSChejunling has typed the table!
A small example: m = 2:
Take a look: 1 It will be found that the data of upper left and lower right, upper right and lower left are the same.
2. The x-th element at the top left and bottom left is always m different.
Well, we can divide it as follows:
//x. y represents the coordinates of the first point of the square, the side length is len, and the value of the first element is z solve(x, y, len - 1, z);///Upper left solve(x + t, y + t, len - 1, z);//lower right solve(x + t, y, len - 1, z + t);//Lower left solve(x, y + t, len - 1, z + t);//Upper right
So, how to solve it?
Obviously, when the square contains only one element, it can be solved directly.
if (len == 0) {
a[x][y] = z;
return ;
}Merge: because the answer is stored in the array when solving, it is equivalent to directly merging into an array.
Full code:
#include <bits/stdc++.h>
using namespace std;
int n, a[40][40];
void solve(int x, int y, int len, int z) {
int t = pow(2, len - 1);
if (len == 0) {
a[x][y] = z;
return ;
}
solve(x, y, len - 1, z);
solve(x + t, y + t, len - 1, z);
solve(x + t, y, len - 1, z + t);
solve(x, y + t, len - 1, z + t);
}
int main() {
cin >> n;
int m = pow(2, n);
solve(1, 1, n, 1);
for (int i = 1;i <= m;i++) {
for (int j = 1;j <= m;j++) {
printf("%d%c", a[i][j], (j != m || i == m) ? ' ' : '\n');
}
}
return 0;
}Quick sort in divide and Conquer:
Algorithm description:
Introduction: first select an element from the data sequence, and put all elements smaller than the element in the sequence to its right or left, and then use the same method for the left and right sides respectively, until the length of each sequence to be processed is 1, and the processing ends.
Examples of pictures and words:
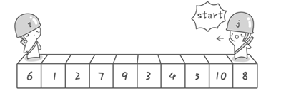
Define double pointers, i = 1, j = n.
Select base number, 6.
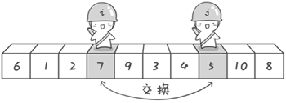
When i finds a number larger than the reference number 6, stop.
When j finds a number smaller than the reference number 6, stop.
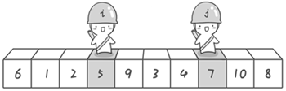
Swap.
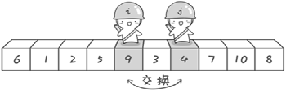
Look again.
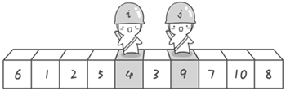
Swap.
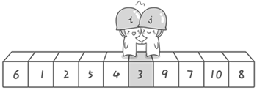
i. j the cycle ends when it coincides.
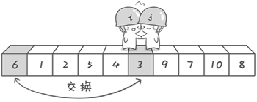
Exchange the reference number with the current number so that the number in front of the reference number is smaller than the reference number and the number behind is larger than the reference number. (reference number homing)
Note that the pointer j moves first.
why?
For example, i and j go too far in the group of data 6 1 2 7 9.
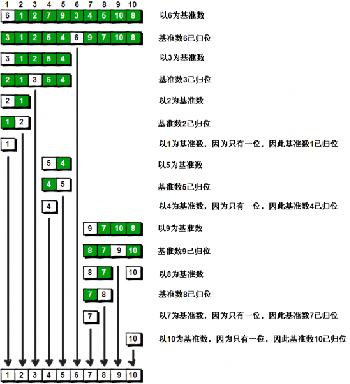
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
int n, a[N];
void qsort(int l, int r) {
if (l >= r) return;
int i = l, j = r, mid = a[i];
while (i != j) {
while (mid < a[j] && i < j) {
j--;
}
while (mid >= a[i] && i < j) {
i++;
}
swap(a[i], a[j]);
}
swap(a[l], a[i]);
qsort(l, i - 1);
qsort(i + 1, r);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
qsort(1, n);
for (int i = 1; i <= n; i++) {
printf("%d ", a[i]);
}
return 0;
}Merge sort in divide and Conquer:
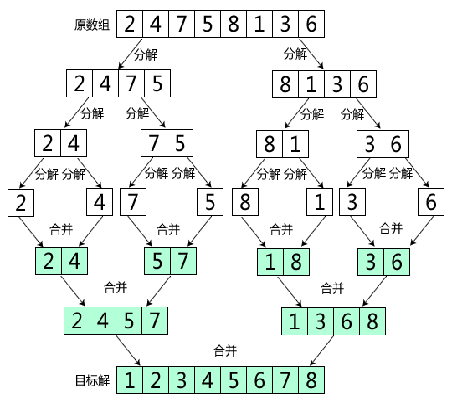
The difference between merging and fast scheduling:
Merging: as shown in the figure above, it is a real divide and conquer algorithm.
Quick platoon: it's just broken down. There's no real point.
code:
#include<iostream>
int n, s1[1000005], s2[1000005];
void merge(int L, int R, int Mid){
int i = L;int j = Mid + 1;int k = L;
while(i <= Mid && j <= R){
if(s1[i] <= s1[j])s2[k ++] = s1[i ++];
else{
s2[k ++] = s1[j ++];
}
}
while(i <= Mid)s2[k ++] = s1[i ++];
while(j <= R)s2[k ++] = s1[j ++];
for(i = L; i <= R; i ++)s1[i] = s2[i];
}
void mergesort(int L, int R){
if(L < R){
int Mid = (L + R) / 2;
mergesort(L, Mid),mergesort(Mid + 1, R);
merge(L, R, Mid);
}
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i ++)scanf("%d", &s1[i]);
mergesort(1, n);
for (int i = 1;i <= n;i++) printf("%d ", s1[i]);
}PS: there is a function of merge. You can refer to this blog: C++ merge function_ Danny Chiu's column - CSDN blog
Summary:
The principle and ranking of the basic test + divide and conquer algorithm.