Sorting algorithm summary
I Exchange sort
1. Bubble sorting
Principle: compare the adjacent elements. If the former is larger than the latter, exchange them. Do the same work for each pair of adjacent elements from front to back. In this way, after a bubble, the last element is the largest number. In this way, each bubble determines the position of an element, and the array is ordered after n times. Similarly, you can bubble from back to front to determine the minimum value in turn.
Bubbling of the original version (unnecessary waste of time will occur if all the numbers have been sorted, but the cycle is not over)
public static void bubble(int []a)
{
if(a.length==0) return ;
int t=a.length;
for(int i=0;i<t-1;i++) //Determine the maximum number in each trip, and each trip (if the position of the number changes) can finally determine the position of a number
{
for(int j=0;j<t-i-1;j++) //Traverse the entire array one by one, except for the number of positions that have been determined
{
if(a[j]>a[j+1]) //In the stone sinking method, if the number in front is greater than the number in the back, the position of the two numbers will be exchanged
{
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}
Improved bubbling method: (marking method)
public static void bubble(int []a)
{
if(a.length==0) return ;
int t=a.length;
boolean flag;
for(int i=0;i<t-1;i++) //Determine the maximum number in each trip, and each trip (if the position of the number changes) can finally determine the position of a number
{
flag=false;
for(int j=0;j<t-i-1;j++) //Traverse the entire array one by one, except for the number of positions that have been determined
{
if(a[j]>a[j+1]) //In the stone sinking method, if the number in front is greater than the number in the back, the position of the two numbers will be exchanged
{
flag=true;
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
if(!flag) break; //There is no position exchange for the numbers in this trip, indicating that all the numbers have been sorted successfully
}
}
Characteristic analysis:
1. Spatial complexity O(1), best time complexity O(n), worst time complexity O(n2), average time complexity O(n2).
2. Bubble sorting is stable (because the numbers exchanged are adjacent): the relative position of numbers of the same type will not change
Application:
1. The final position of a number can be determined by each sequence of bubbling, which is suitable for finding the first n large (small) numbers in large-scale data, that is, n external cycles
2. Using the stability of bubbling, the relative position of the same type of data can not be changed when operating a group of data For example, put all odd numbers before even numbers in an array without changing the relative position
2. Quick sort
Principle: the principle of quick sorting is to first find a center, put the value less than the center in front of him and the value greater than the center to his right, then quickly sort the two parts of data in this way, and then quickly sort the two parts of data in this way. The whole sorting process can be recursive, In this way, the whole data becomes an ordered sequence.
Basic idea:
Fast sorting algorithm is a sorting algorithm based on divide and conquer strategy. Its basic idea is to sort the input array a[low, high] according to the following three steps.
(1) Decomposition: Based on a[p], a[low: high] is divided into three sections a[low: p-1], a[p] and a[p+1: high], so that any element in a[low: p-1] is less than or equal to a[p], and any element in a[p+1: high] is greater than or equal to a[p].
(2) Recursive solution: sort a[low: p-1] and a[p+1: high] respectively by recursively calling the quick sort algorithm.
(3) Merge: since the sorting of a[low: p-1] and a[p+1: high] is performed locally, after both a[low: p-1] and a[p+1: high] have been ordered, there is no need to perform any calculation, and a[low: high] has been ordered.
public static void quicksort(int []a,int left,int right) //Fixed datum, taking the middle number as an example
{
if(a.length==0||left>=right) return ;
int mid=a[(left+right)/2];
int i=left;
int j=right;
while(i<=j)
{
while(i<=j&&a[i]<mid) i++;
while(i<=j&&a[j]>mid) j--;
if(i<=j)
{
int temp=a[i];
a[i]=a[j];
a[j]=temp;
i++;
j--;
}
} //After jumping out of the loop, the left side of i is the number less than mid, and the right side of j is the number greater than mid
quicksort(a,left,j);
quicksort(a,i,right);
}
public static int partion(int []a,int left,int right) //Excavation method
{
if(a.length==0||left>=right) return -1;
int i=left;
int j=right;
int pet=a[left];
while(i<j)
{
while(i<j&&a[j]>pet) j--;
if(j<=i) break;
a[i]=a[j];
while(i<j&&a[i]<=pet) i++; //When jumping out of the loop, the numbers to the left of i are < = pet
if(j<=i) break; //Cross the border, all the numbers have been searched
a[j]=a[i];
} //When i==j, it is the position of the cardinality
a[i]=pet;
return i;
}
public static void quicksort_(int []a,int left,int right) //Excavation method
{
if(a.length==0||left>=right) return ;
int pos= partion(a,left,right);
quicksort_(a,left,pos-1);
quicksort_(a,pos+1,right);
}
This practice is a bit similar to the double pointer idea. Each trip is divided into two different ranges, and then further sorted, reflecting the idea of divide and conquer
Application: get the smallest number of k
public static int partion(int []a,int left,int right) //Pit excavation method, carry out a round of division, and determine the final position of a number in each round
{
if(a.length==0||left>=right) return -1;
int i=left;
int j=right;
int pet=a[left]; //Select the leftmost number as the base
while(i<j)
{
while(i<j&&a[j]>pet) j--; //When jumping out of the loop, the right side of j is a number greater than the cardinality
if(j<=i) break;
a[i]=a[j];
while(i<j&&a[i]<=pet) i++; //When jumping out of the loop, the numbers to the left of i are < = pet
if(j<=i) break; //Cross the border, all the numbers have been searched
a[j]=a[i];
} //When i==j, it is the position of the cardinality
a[i]=pet;
return i;
}
public static int quicksort_(int []a,int left,int right,int k) //Pit digging method to obtain the smallest number of k
{
if(left==right&&k==1) return a[left];//Recursion end condition: when the array has only one number and k=1
int pos= partion(a,left,right);
int tem=pos-left+1;//Quantity less than or equal to the number of selected cardinalities per trip
if(k<=tem) return quicksort_(a,left,pos,k);
else return quicksort_(a,pos+1,right,k-tem);
}
Characteristic analysis:
(1) The best time complexity is O(nlog2n), the worst is n ^ 2 (degenerate into a single branch tree, basically because of the selection of cardinality) and the space complexity is O(log2n)
(2) The sorting algorithm is unstable and cannot guarantee that the relative position of numbers of the same type will not change after sorting
(3) This algorithm has the highest efficiency in the case of huge data scale and complete disorder Poor performance in dealing with small-scale data At this time, you can use insert sort instead.
(4) Quick sort adopts a divide and conquer strategy, which is usually called divide and conquer. Now many sorting libraries in various languages use quick sort. This divide and conquer can be applied to a variety of situations, such as obtaining the smallest number k
Improvement method: (for pivot selection)
1. Select a random number as the pivot.
2. Use the median of the left end, right end and center as the pivot element.
3. Select the median in the data set as the pivot each time.
Insert sort
1. Direct insertion sorting
Basic idea: insert a record to be sorted into the ordered data according to the size of its keyword in each step until all the records are inserted.
public static void insertsort(int []a)
{
if(a.length==0) return ;
for(int i=0;i<a.length;i++) //Each pass inserts a[i] into the previous sort subsequence
{
int temp=a[i];
int j=i-1;
while(j>=0&&temp<a[j]) //If the preceding number is greater than a[i], the position is swapped
{
a[j+1]=a[j];
j--;
}
a[j+1]=temp;
}
}
2. Sort by half insertion
On the basis of direct insertion sorting, if the amount of data is relatively large, in order to reduce the number of key comparison, you can use half insertion to find the position to be inserted. However, the time complexity O(n^2) and space complexity O(1) of the algorithm are still not changed The algorithm is stable
public static int Binary(int []a,int index,int x) //Find the first number greater than x in the array, that is, the insertion position
{
int left=0;
int right=index;
while(left<=right)
{
int mid=(left+right)/2;
if(a[mid]>x)
{
right=mid-1;
}
else left=mid+1;
}
return left;
}
public static void insertsort(int []a)
{
if(a.length==0) return ;
for(int i=0;i<a.length;i++)
{
int temp=a[i];
int j=i-1;
if(j>=0)
{
int ans=Binary(a,j,temp);
//System.out.println(ans);
for(int k=j;k>=ans;k--) //Move ans and the following numbers to the next digit
{
a[k+1]=a[k];
}
a[ans]=temp; //Filling number
}
}
}
Insertion sorting is applicable to the case where some data are ordered. The larger the ordered part, the better.
Select sort
Simple selection sort
Its working principle is to select the smallest (or largest) element from the data elements to be sorted every time and store it at the beginning of the sequence until all the data elements to be sorted are finished.
public static void simpleSelectSort(int []a)
{
if(a.length==0) return ;
int min;
for(int i=0;i<a.length-1;i++)
{
min=i;
for(int j=i+1;j<a.length;j++)
{
if(a[j]<a[min])
{
min=j;//Record the subscript of the minimum value
}
}
if(min!=i) //Find the minimum value in the following number and exchange
{
int temp=a[i];
a[i]=a[min];
a[min]=temp;
}
}
}
Characteristic analysis:
1. Spatial complexity O(1), best / worst / average time complexity O(n2), comparison times O(n2), movement times O(n).
2. Selective sorting is an unstable sorting method
Merge sort
Merge sort is an effective sorting algorithm based on merge operation. It is a very typical application of Divide and Conquer. Merge the ordered subsequences to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging.
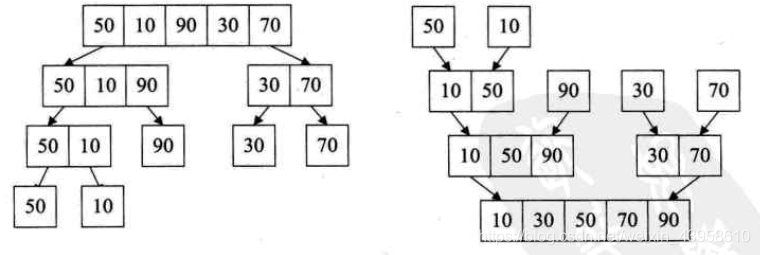
public static void Mergesort(int []a,int []b,int start,int end)
{
if(a.length==0) return ;
if(start==end)
{
b[start]=a[start];
return ;
}
int mid=(start+end)/2; //Take the middle point
Mergesort(a,b,start,mid); //Order the left part of the array
Mergesort(a,b,mid+1,end);//Order the right part of the array
int i=start;
int j=mid+1; //Double pointer
int t=start;
while(i<=mid&&j<=end)
{
if(i<=mid&&a[i]<=a[j])
{
b[t++]=a[i++];
}
if(j<=end&&a[j]<=a[i])
{
b[t++]=a[j++];
}
}
while(i<=mid) b[t++]=a[i++];
while(j<=end) b[t++]=a[j++];
for(int k=start;k<=end;k++)
{
a[k]=b[k];
}
}
Characteristic analysis:
1. The best, worst and average time complexity of merging and sorting are o (n l o g n), and the space complexity is O(n)
2. Because it requires pairwise comparison of elements, there is no jump, so merge sorting is a stable sorting algorithm, but the recursive merge sorting requires a large amount of additional space, while the iterative implementation is relatively small and the running time overhead is also small. Therefore, the iterative method should be used as much as possible.
3. The algorithm embodies the idea of divide and conquer, but it is different from fast sorting The algorithm can be compared with the post - order traversal of a tree
Application scenario:
Find the number of pairs in reverse order in an array
Why do reverse order pairs use merge sort?
The algorithm is calculated from bottom to top. The premise of each merging is that the two groups of arrays are orderly. Calculate the initial reverse pairs of the two arrays before merging, and then merge It's actually a bit greedy to find the reverse order in the two-part ordered array In essence, it is also divide and conquer (big problems are broken down into small problems)
static int ans=0;
public static void Mergesort(int []a,int []b,int start,int end)
{
if(a.length==0) return ;
if(start==end)
{
b[start]=a[start];
return ;
}
int mid=(start+end)/2; //Take the middle point
Mergesort(a,b,start,mid); //Order the left part of the array
Mergesort(a,b,mid+1,end);//Order the right part of the array
int i=start;
int j=mid+1; //Double pointer
int t=start;
while(i<=mid&&j<=end) //The left and right pointers move once respectively
{
if(a[i]<=a[j])//The movement of the left pointer '=' is because two identical numbers are not in reverse order
{
b[t++]=a[i++];
}
else if(a[j]<a[i]) //For the movement of the right pointer, the number of reverse order pairs needs to be recorded only when the right pointer moves
{
b[t++]=a[j++];
ans+=(mid-i+1); //The number of the left part of the array greater than a[j], and the movement of each right pointer shall be calculated
}
}
while(i<=mid) b[t++]=a[i++];
while(j<=end) b[t++]=a[j++];
for(int k=start;k<=end;k++)
{
a[k]=b[k];
}
Heap sort
The structure of heap can be divided into large root heap and small root heap. It is a complete binary tree, and heap sorting is a sort designed according to the data structure of heap
Definition and nature of heap:
Large root pile: arr (I) > arr (2I + 1) & & arr (I) > arr (2I + 2)
Small root pile: arr (I) < arr (2I + 1) & & arr (I) < arr (2I + 2)
Basic idea:
1. First, construct the array to be sorted into a large root heap. At this time, the maximum value of the whole array is the top of the heap structure
2. Exchange the number at the top with the number at the end. At this time, the number at the end is the maximum and the number of remaining arrays to be sorted is n-1
3. Reconstruct the remaining n-1 numbers into a large root heap, and then exchange the top number with the number at the N-1 position. The position of a number (the largest in n-1) can be determined in each trip. After repeated execution, an ordered array can be obtained
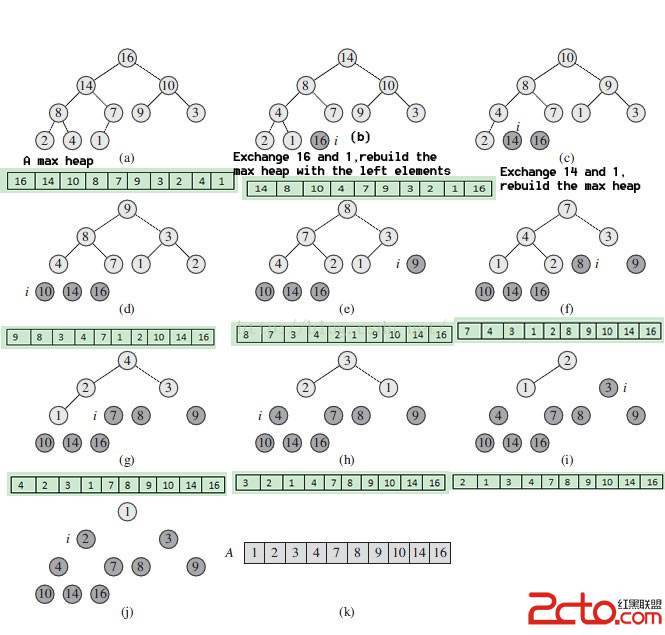
public static void headsort(int []a)
{
if(a.length==0) return ;
for(int t=a.length/2-1;t>=0;t--) //Adjust from the first non leaf node
{
adjust(a,t,a.length);
}
for(int t=a.length-1;t>0;t--) //The maximum number is determined for each trip and placed at the end of the array
{
swap(a,0,t);
adjust(a,0,t);
}
}
public static void adjust(int []a,int i,int length)//Adjust to large root heap within [i,length)
{
int t=length;
int ans=a[i];
int j=i; //j indicates where a[i] should be inserted
for(int k=2*i+1;k<t;k=2*k+1) //Traverse left child
{
if(k+1<t&&a[k]<a[k+1]) //Determine the biggest point of the left and right children
{
k++;
}
if(a[k]>ans)
{
a[j]=a[k];
j=k;
}
else break; //Find the final a[i] place to insert
}
a[j]=ans;
}
public static void swap(int []a,int i,int j)
{
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
Characteristic analysis:
1. Space complexity O(1), average time complexity O (n log n), adjust the heap O(log n) - that is, the height of the heap. Due to the large number of comparisons required to build the initial heap, heap sorting is not suitable for the case with a small number of records.
2. Heap sorting is unstable.