Implementation, connection and difference of prim & Dijkstra & Floyd algorithm && using Floyd algorithm to find sub short path
catalogue
Prim & Dijkstra L & Floyd, these algorithms are actually a handsome group, that is, the data structure class is too disgusting (I know everything), and I don't really realize the beauty of these algorithms. After the exam, I suddenly want to write an article to knead these algorithms together, which is my unfinished wish.
from the bottom of one's heart
The main reason is that I originally wanted to use CSDN to speed up the algorithm in a very short review time, but the same article was constantly reprinted and transported, and a large number of drainage marketing numbers were in water articles, resulting in the efficiency of online search algorithm analysis is not as high as that of reading, which indirectly led to the rollover of the exam. Who can bear it? I had to write a hodgepodge by myself so that latecomers would not jump into the pit I had jumped into because there was too little high-quality content
Basic knowledge
First of all, Prim and Dijkstra algorithms have the same theoretical basis - MST property, to the effect that * * suppose there is a connected network, all nodes form a set G, for a true subset U of G, if one edge e is the shortest edge satisfying the condition of "one endpoint is in U, the other endpoint is in G but not in U", Then there must be a minimum spanning tree of G containing edge E** I'm not good at math. I won't prove it here.
Algorithm details
1, Prim algorithm
1. Text description
Starting from any vertex, first add the vertex to the spanning tree T, then select the edge with the shortest length among the edges where all endpoints are in the tree and one endpoint is not in the tree, and then add the node corresponding to this edge and edge to the spanning tree, and so on until all nodes are added to the spanning tree.
2. Structure determination
Determine the relevant storage structure
struct edge
{
int vi, vj; // Start and end of edge
int weight; // weight
};
int w_matrix[n][n]; // adjacency matrix
edge T[n - 1]; // Record minimum spanning tree
3. Process demonstration
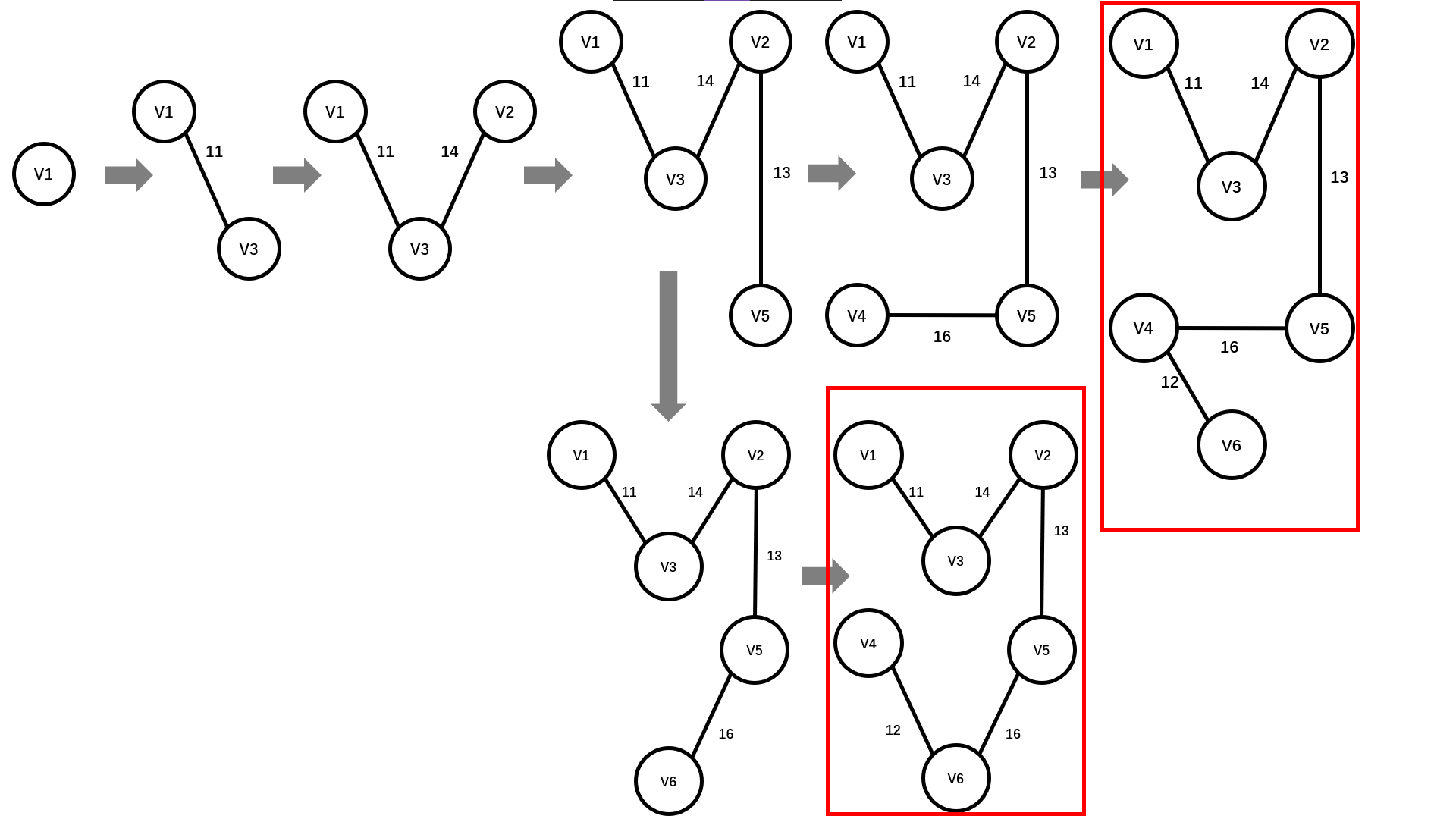
4. Parsing code
void prim(edge T[6]) //
{
int m, v, min;
edge e;
// Initialize edge array
for (int i = 1; i < 6; i++)
{
T[i - 1].vi = 1;
T[i - 1].vj = i + 1;
T[i - 1].weight = w_mtx[0][i];
}
//Find the edge of the i + 1 minimum spanning tree
for (int i = 0; i < 5; i++) // The minimum spanning tree has 6 - 1 = 5 edges
{
min = INFI;
//Select the edge with the smallest weight from T[i] to T[n - 2] to join the minimum spanning tree
for (int j = i; j < 5; j++)
{
if (T[j].weight < min)
{
min = T[j].weight;
m = j;
}
}
//Move the selected edge with the shortest weight to the front
e = T[m]; T[m] = T[i]; T[i] = e;
//The vertex sequence number corresponding to the newly added edge
v = T[i].vj;
//Update the edge table. In the example above, compare the length of V1 VN with the value of V3 VN
//In this way, the shortest edges with one endpoint in the set and one endpoint outside the set are always saved in the table
int d = 0;
for (int k = i + 1; k < 5; k++)
{
d = w_mtx[v - 1][T[k].vj - 1];
if (d < T[k].weight)
{
T[k].weight = d;
T[k].vi = v;
}
}
}
}
5. Operation results
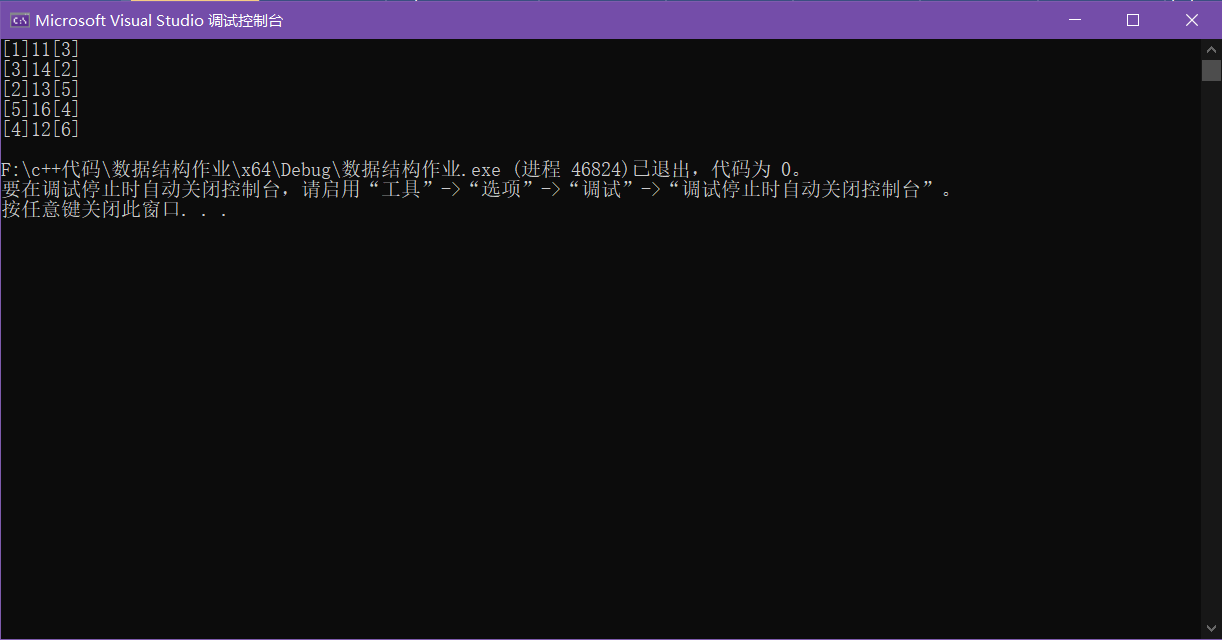
2, Dijkstra algorithm
1. Text description
The basic operation of the method is: divide the vertex set V of the graph into two groups A and B, in which the shortest path from the origin to the vertices in group A has been determined, and the vertices in group B have not been determined. Initially, there is only the starting point in a, and then select the node closest to the starting point from B to join a. At this time, update the edge table: take the newly added node as the starting point, traverse the distance from the new node to all other nodes in B, and find the point with the shortest path among the points adjacent to it. For example, add this point to set a until all nodes enter a.
2. Structure determination
Determine the relevant storage structure
struct path
{
int pre; // The previous node added to A
int length; // weight
};
int w_mtx[n][n]; // adjacency matrix
path dist[]; // Record minimum path tree
3. Process demonstration
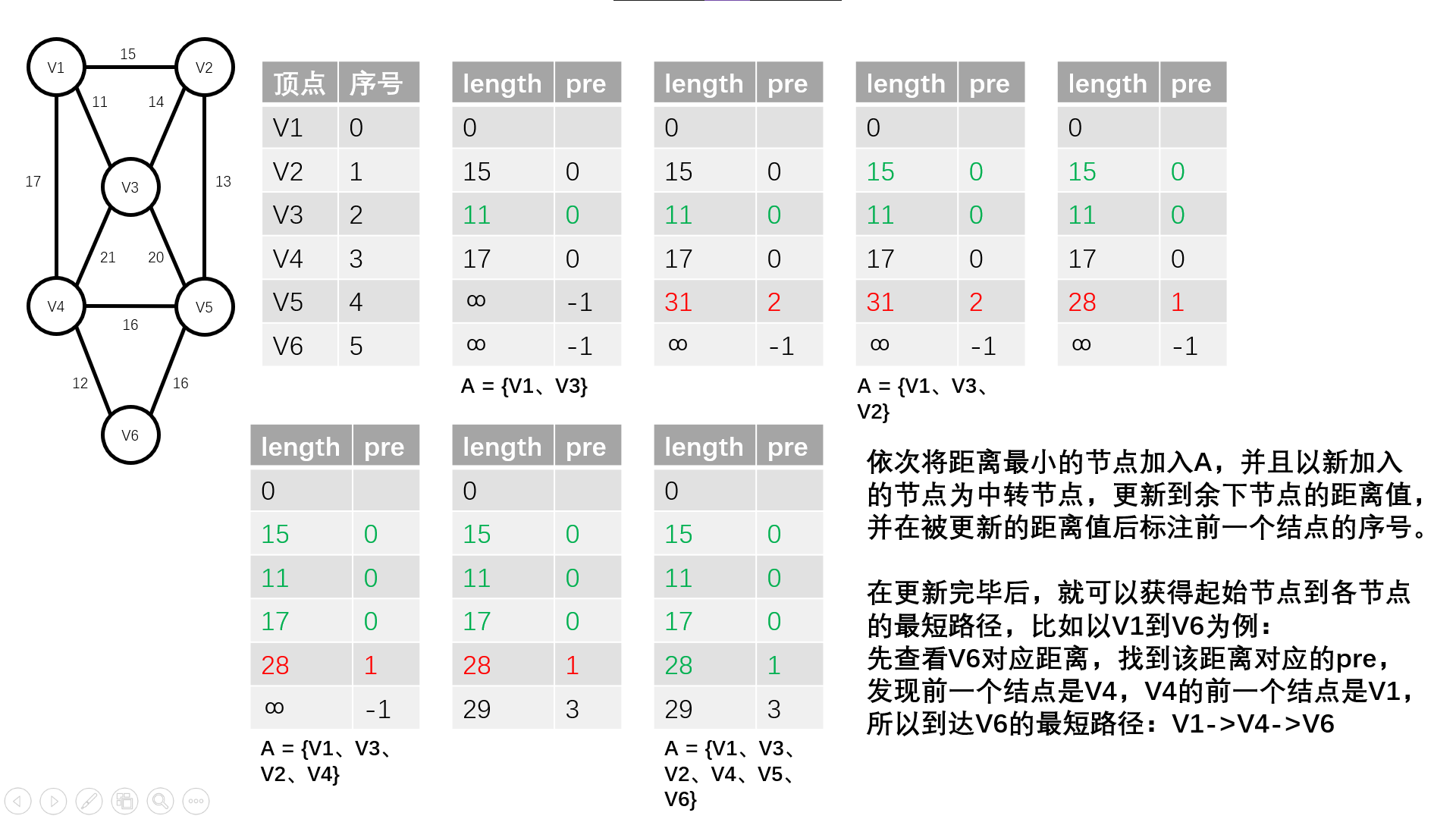
4. Code parsing
Here is another use case that can better reflect the difference between Dijkstra algorithm and Prim algorithm. I will analyze the difference between the two algorithms in detail in later articles
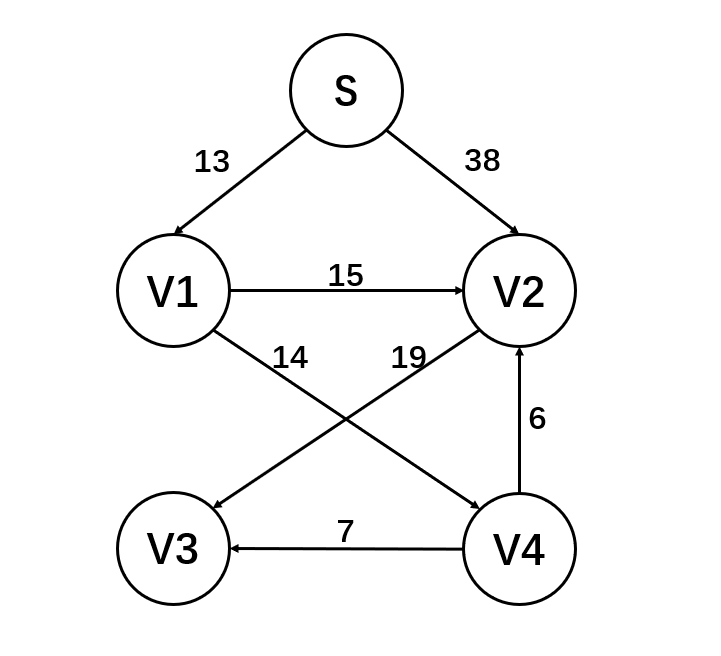
void dijkstra(path dist[], int s) //s is the origin sequence number
{
int i, u, min;
// Initialize dist array
for(i = 0; i < 5; i++)
{
dist[i].length = w_mtx[s][i];
if (dist[i].length == INFI)
{
dist[i].pre = -1;
}
else
{
dist[i].pre = s;
}
}
w_mtx[i][i] = 1; // Mark nodes that have joined A
//Add nodes to A in order
while (1)
{
u = -1;
min 5, INFI;
for (i = 0; i < 5; i++)
{
if (w_mtx[i][i] == 0 && dist[i].length < min)
{
min = dist[i].length;
u = i;
}
}
if (u == -1)
{
// If all nodes have joined A(w_mtx[i][i]=0),
// Or the remaining nodes are unreachable (dist[i].length=INFI),
// Then end the algorithm
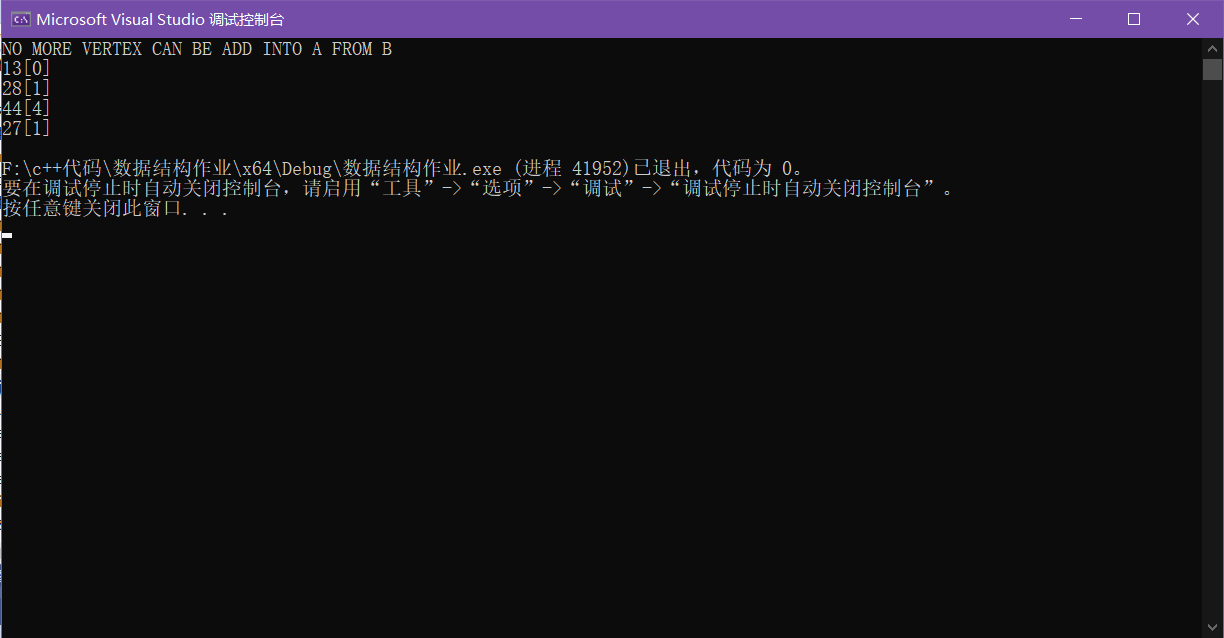
cout << "NO MORE VERTEX CAN BE ADD INTO A FROM B" << endl;
return;
}
w_mtx[u][u] = 1;
//Update distance
for (i = 0; i < 5; i++)
{
if (w_mtx[i][i] == 0 && dist[i].length > dist[u].length + w_mtx[u][i])
{
dist[i].length = dist[u].length + w_mtx[u][i];
dist[i].pre = u;
}
}
}
}
5. Operation results
3, Floyd algorithm
I found a very detailed tutorial on this algorithm on the Internet, which is concise and clear. Here, I decide to let more professional people do professional things. The link is shown as follows:
Freudian algorithm that a fool can understand (turn)
I can't find the original blog of this article, and I'm not sure whether the link above is the original blog. In short, the above one is the earliest one published in Baidu search. Just make do with it. It's just bitter for the original author.
Feel the current suffocating atmosphere of reprinting on the Internet
My code is posted below:
1. Data structure
Note: Here I introduce a path matrix to store the path, because the algorithm of the above author only outputs the shortest distance, so it is impossible to know the path
int path[n][n];
Storage rule: if W_ The data in the matrix is modified, and the data corresponding to the path is modified to the number of the previous node

2. Code analysis
The following is pseudo code
#define INFI 10000
int path[n][n];
void Floyd(int D[n][n], int w_mtx[n][n])
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(w_mtx[i][j] != INFI) path[i][j] = i + 1;
else path[i][j] = 0;
D[i][j] = w_mtx[i][j];
}
for(int k = 0; k < n; k++)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(D[i][j] > D[i][k] + D[k][j]) // Core code
{
D[i][j] = D[i][k] + D[k][j];
path[i][j] = path[k][j]; // Update path
}
}
}
}
}
}
Algorithm similarities and differences
Find a well written article to clarify this problem
Flow saving:
Prim algorithm is used to construct the minimum spanning tree - that is, the sum of the weights of all edges in the tree is the minimum. For example, build a circuit board to minimize the and cost of all edges. Can only be used for undirected graphs.
Dijkstra algorithm is used to construct the shortest path tree (MST) of single source point - that is, the distance from a point in the tree to any other point is the shortest. For example, when building a map application, find the shortest distance between your coordinates and a landmark. It can be used for directed graphs, but there cannot be negative weights (Bellman Ford can handle negative weights).
Floyd algorithm for secondary short path
Written by a classmate from an ACM boss
#include<iostream>
#include<cstdio>
#include<stack>
#define ma 100000000
using namespace std;
stack<int> out;
int n, adj[35][35][2], path[35][35][2];
void floyd_change()
{
for(int k = 1; k <= n; k++)
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
if(i == k || j == k)
continue;
int a, b;
if((adj[i][k][0] + adj[k][j][0]) < adj[i][j][0])
{
adj[i][j][1] = adj[i][j][0];
path[i][j][1] = path[i][j][0];
adj[i][j][0] = adj[i][k][0] + adj[k][j][0];
path[i][j][0] = path[k][j][0];
if((adj[i][k][0] + adj[k][j][1]) < (adj[i][k][1] + adj[k][j][0]))
{
a = 0;
b = 1;
}
else
{
a = 1;
b = 0;
}
if((adj[i][k][a] + adj[k][j][b]) < adj[i][j][1])
{
adj[i][j][1] = adj[i][k][a] + adj[k][j][b];
path[i][j][1] = path[k][j][b];
}
}
else if((adj[i][k][0] + adj[k][j][0]) < adj[i][j][1] && path[k][j][0] != path[i][j][1])
{
adj[i][j][1] = adj[i][k][0] + adj[k][j][0];
path[i][j][1] = path[k][j][0];
}
}
}
}
}
int main()
{
cout << "Please enter the number of nodes\n";
cin >> n;
cout << "Please enter adjacent matrix, positive infinity-1 Indicates that other paths must be less than 100000\n";
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
scanf("%d", &adj[i][j][0]);
if(adj[i][j][0] == -1)
adj[i][j][0] = ma;
adj[i][j][1] = ma;
path[i][j][0] = i;
path[i][j][1] = -1;
}
}
floyd_change();
cout << "Please enter the starting point and ending point of the path for each round of query in turn. Both the starting point and ending point are-1 End query at\n";
int a, b;
while(cin >> a >> b)
{
if(a == -1 && b == -1)
break;
cout << "Next, the first line is the shortest path length and path, and the second line is the second short path length and path(-1 Represents no path):\n";
if(adj[a][b][0] == 100000000)
cout << -1 <<endl;
else
{
cout << adj[a][b][0] << " : ";
int tmp = b;
while(tmp != a)
{
out.push(tmp);
tmp = path[a][tmp][0];
}
out.push(a);
while(out.size())
{
cout << out.top() << " ";
out.pop();
}
cout << endl;
}
if(adj[a][b][1] == 100000000)
cout << -1 <<endl;
else
{
int f = 0;
cout << adj[a][b][1] << " : ";
int tmp = b;
out.push(b);
while(tmp != a)
{
if(path[a][tmp][1] != path[a][tmp][0] && !f)
{
f = 1;
tmp = path[a][tmp][1];
}
else
tmp = path[a][tmp][0];
out.push(tmp);
}
if(tmp == a && path[a][tmp][1] != a && !f)
{
tmp = path[a][tmp][1];
out.push(tmp);
while(tmp != a)
{
tmp = path[a][tmp][0];
out.push(tmp);
}
}
while(out.size())
{
cout << out.top() << " ";
out.pop();
}
cout << endl;
}
}
return 0;
}