View this article on your personal blog
Two problems to be dealt with in parallel search set
- query
Query whether two vertices in the graph are in the same set.
- merge
Merge two disjoint sets.
Two ideas of designing and searching sets
- Based on id
Each vertex is assigned a unique identifier called id
Different IDS come from different sets.
When merging, you need to assign the IDs of all elements in one set to the IDs of the other set. You need to traverse the id of the entire collection.
- Based on parents
Instead of using IDs to divide collections, they are divided according to their parent nodes. parent[i] indicates the identification of the parent node of the node identified as I (it can be vividly recorded as "looking for father"). Under this definition, the parent node of the root node is itself. The "join query set" formed in this way is organized into several disjoint tree structures, and we always access nodes "from bottom to top".
Representative element method
"Three unimportant" of "representative yuan"
-
It doesn't matter who is the root node: the root node and non root node are just in different positions and have no additional meaning;
-
It doesn't matter how the tree is formed: when merging, the root node of any set can point to another combined root node;
-
The shape of the tree is not important: the reason is the same as "who is the root node is not important".
Possible problems caused by representative element methodThe height of the tree is too high and the query performance is reduced.
Solutions include rank merging and path compression.
Merge by rank
Merging by rank generally refers to pointing the root node with smaller rank to the root node with more rank.
Rank here has two meanings:
- size merge
- rank merge
Merge by size
Let the root node of the tree with a smaller total number of nodes point to the root node of the tree with a larger total number of nodes.
Merge by rank
Merging by rank means that the root node of the tree with smaller "height" of the tree points to the root node of the tree with larger "height".
The reason why "height" is called rank is that when "merging by rank" and "path compression" are used at the same time, the "height" of the tree is difficult to maintain its accurate definition, but it can still be used as the basis for merging, so it is called "rank".
Path compression
Intergenerational compression
Two steps and one jump, always loop [point the current node to the parent node of its parent node]
Complete compression
Point all nodes passing from [query node] to [root node] to the root node. [complete compression] is more thorough than [alternate generation compression].
Code template
class UnionFind {
int[] parent;
int n;
public UnionFind(int n) {
this.n = n;
this.parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public void unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return;
}
parent[y] = x;
}
}
The use of concurrent query set includes two operations, query and merge.
- Use findset method to realize and query set. parent[x] == x ? X: (parent [x] = findset (parent [x]) find the parent node of X.
If x is the root node, there is parent[x] == x, otherwise we will continue to find the parent node of X's father. That is, parent[x] = findset(parent[x])
- Use the unite method to merge sets. First, determine whether the two elements are in the same set, and use findset to find out whether they have a common parent node.
x = findset(index1);
y = findset(index2);
if (x == y) {
return;
}
If they have a common parent node, it is proved that they are in a set and do not need to be merged. If there is no common parent node, we only need to overwrite the parent node of another element. parent[y] = x.
Basic issues
Satisfiability of equation
990. Satisfiability of equation
Given an array of string equations representing the relationship between variables, the length of each string equation [i] is 4 and takes one of two different forms: "a==b" or "a!=b". Here, a and b are lowercase letters (not necessarily different), representing single letter variable names.
Returns true only if an integer can be assigned to a variable name to satisfy all given equations; otherwise, returns false.
Example 1:
Input: ["a==b","b!=a"]
Output: false
Explanation: if we specify that a = 1 and b = 1, the first equation can be satisfied, but the second equation cannot be satisfied. There is no way to assign variables that satisfy both equations.
Example 2:
Input: ["b==a","a==b"]
Output: true
Explanation: we can specify a = 1 and b = 1 to satisfy these two equations.
Example 3:
Input: [a==b","b==c","a==c "]
Output: true
Example 4:
Input: [a==b","b!=c","c==a "]
Output: false
Example 5:
Input: [c==c","b==d","x!=z "]
Output: true
Tips:
- 1 <= equations.length <= 500
- equations[i].length == 4
- equations[i][0] and equations[i][3] are lowercase letters
- equations[i][1] either '=' or ` '!'``
- ``equations[i][2] is' = '`
The key point of this question is how to turn the question into and search the set. Due to the existence of a = = B, B = = a, B= C for this kind of relationship, we can regard = = as a connection relationship, and= As a non Unicom relationship, we only need to establish the Unicom relationship and non Unicom relationship according to the known conditions to determine whether there is a contradictory relationship.
As for the establishment of joint search set, there are lowercase letters such as a, B, C and D, and the topic variable has and only lowercase letters and == Therefore, the length of parent [] in the union set we established is 26
The title code is as follows:
class Solution {
public boolean equationsPossible(String[] equations) {
UnionFind uf = new UnionFind(26);
for(String str : equations){
if(str.charAt(1)=='='){
int index1 = str.charAt(0) - 'a';
int index2 = str.charAt(3) - 'a';
uf.unite(index1, index2);
}
}
for(String str : equations){
if(str.charAt(1)=='!'){
int index1 = str.charAt(0) - 'a';
int index2 = str.charAt(3) - 'a';
if(uf.findset( index1) ==
uf.findset(index2)){
return false;
}
}
}
return true;
}
}
class UnionFind {
int[] parent;
int n;
public UnionFind(int n) {
this.n = n;
this.parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public void unite(int index1, int index2) {
index1 = findset(index1);
index2 = findset(index2);
if (index1 == index2) {
return;
}
parent[index2] = index1;
}
}
Number of provinces
Number of provinces
There are n cities, some of which are connected to each other, others are not connected. If city a is directly connected to city b and city b is directly connected to City c, city a is indirectly connected to city c.
A province is a group of directly or indirectly connected cities, excluding other cities that are not connected.
Give you an n x n matrix isConnected, where isConnected[i][j] = 1 indicates that the ith city and the jth city are directly connected, and isConnected[i][j] = 0 indicates that they are not directly connected.
Returns the number of provinces in the matrix.
Example 1:
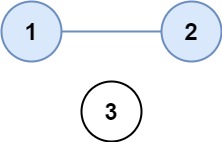
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]] Output: 2
Example 2:
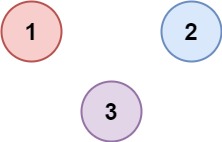
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]] Output: 3
Tips:
- 1 <= n <= 200
- n == isConnected.length
- n == isConnected[i].length
- isConnected[i][j] is 1 or 0
- isConnected[i][i]== 1
- isConnected[i][j] == isConnected[j][i]
The example of this problem gives the picture. We can determine that it is a graph theory problem, and the main direction of this problem is the connectivity problem. Therefore, we can safely use and search sets to solve the problem. The problem is that there are several provinces. The province is a group of directly or indirectly connected cities, and the group does not include other cities that are not connected. Then it is transformed into a joint search set problem to solve how many sets there are in the joint search set. We only need to solve a few trees.
The idea is to query the parent node of the current node. Merge nodes with the same parent node. Determine the number of trees.
The code is as follows:
class Solution {
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
UnionFind uf = new UnionFind(n);
//Query and merge collections
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
if(isConnected[i][j]==1){
uf.unite(i, j);
}
}
}
//Calculate the number of trees
int cnt = 0;
for(int i = 0; i < n; i++){
if(uf.parent[i] == i){
cnt++;
}
}
return cnt;
}
}
class UnionFind {
int[] parent;
int n;
public UnionFind(int n) {
this.n = n;
this.parent = new int[n];
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public void unite(int index1, int index2) {
index1 = findset(index1);
index2 = findset(index2);
if (index1 == index2) {
return;
}
parent[index2] = index1;
}
}
Redundant link
684. Redundant connection
The tree can be regarded as a connected and acyclic undirected graph.
Given a graph after adding an edge to a tree with n nodes (node values 1 ~ n). The two vertices of the added edge are contained between 1 and N, and the additional edge does not belong to the existing edge in the tree. The information of the graph is recorded in the two-dimensional array edges with length n. edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.
Please find an edge that can be deleted. After deletion, the remaining part can be a tree with n nodes. If there are multiple answers, the last edge in the array edges is returned.
Example 1:

input: edges = [[1,2], [1,3], [2,3]] output: [2,3]
Example 2:
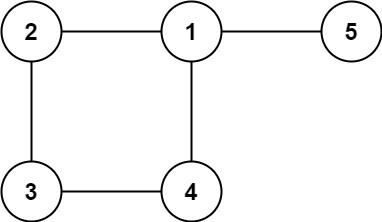
input: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] output: [1,4]
Tips:
- n == edges.length
- 3 <= n <= 1000
- edges[i].length == 2
- 1 <= ai < bi <= edges.length
- ai != bi
- No duplicate elements in edges
- A given graph is connected
Very common undirected graph connectivity problem. The purpose of this topic is to let us deal with the problem of undirected graph looping. That is, we need to find the last edge that makes the undirected graph ring according to the edges in the known conditions.
Consider how the ring is formed:
If the two vertices belong to different connected components (i.e. different sets), it means that the two vertices are not connected before traversing the current edge, so the current edge will not cause the ring to appear, and the connected components of the two vertices will be merged.
If two vertices belong to the same connected component (the same set), it means that the two vertices have been connected before traversing the current edge, so the current edge causes the ring to appear. It is an additional edge, and the current edge is returned as the answer.
It is worth noting that our edges start from 1 to N. therefore, when establishing parent [], we should set its length to n+1 and the contents of nodes are 1~n respectively.
The code is as follows:
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
UnionFind uf = new UnionFind(n);
for(int i = 0; i < n; i++){
int[] edge = edges[i];
int node1 = edge[0], node2 = edge[1];
if(uf.findset(node1)!= uf.findset(node2)){
uf.unite(node1, node2);
}
else{
return edge;
}
}
return new int[0];
}
}
class UnionFind {
int[] parent;
public UnionFind(int n) {
this.parent = new int[n+1];
for (int i = 0; i <= n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public void unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return;
}
parent[y] = x;
}
}