GitHub sync update (Classified): Data_Structure_And_Algorithm-Review (it's best to give a star!!!)
The following is the main body of this article, and the following cases can be used for reference.
Traversal of binary tree
Traversing a binary tree is to access each node in the binary tree successively and only once according to a search path.
Access has a wide meaning, such as output, search, insert, delete, modify, operation and so on. Traversal is performed sequentially.
A binary tree is composed of root, left subtree and right subtree.
According to the access order of root, left subtree and right subtree, there are six schemes for traversing binary tree:
D
L
R
,
L
D
R
,
L
R
D
,
D
R
L
,
R
D
L
,
R
L
D
DLR,LDR,LRD,DRL,RDL,RLD
DLR,LDR,LRD,DRL,RDL,RLD
If left before right is limited (left subtree before right subtree), there are only the first three traversal schemes: DLR, LDR and LRD.
The traversal order (LRR) and the access order (DLR) in different traversal order are respectively called LRR and DLR.
Because the definition of tree itself is recursive, the basic operation of tree and binary tree recursive algorithm is easy to implement.
But... It's so simple, it's not good.
Start with recursive code.
Recursive code
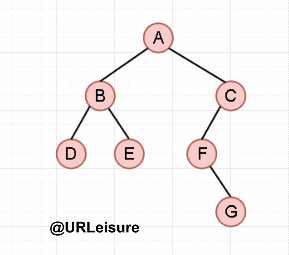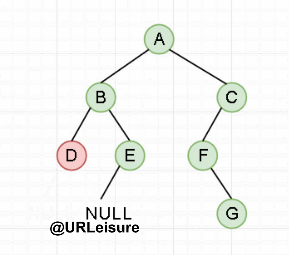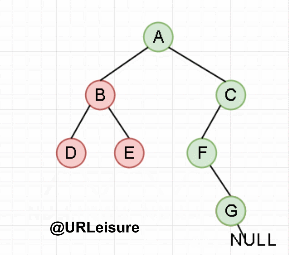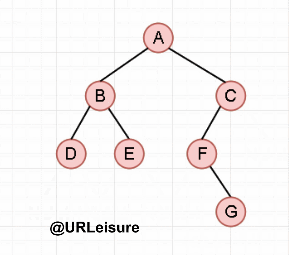
Take the binary tree as an example:
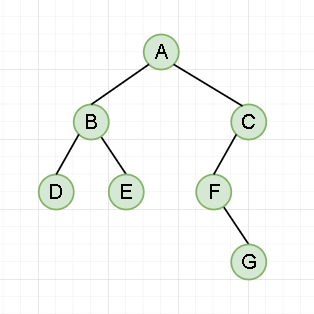
Preorder traversal
Algorithm steps:
If the binary tree is not empty:
- Access the root node;
- Traversing the left subtree first;
- First traverse the right subtree.
{repeat the node access and left recursion until you reach the leftmost child, and then right once; repeat the previous operation (right is empty, this level recursion ends, and returns to the previous level)}
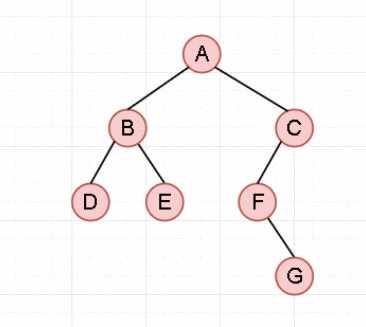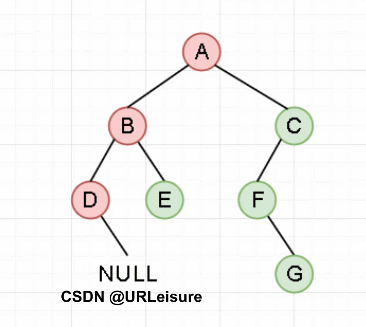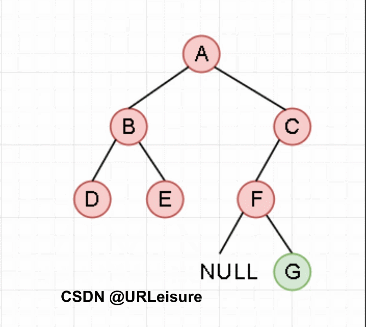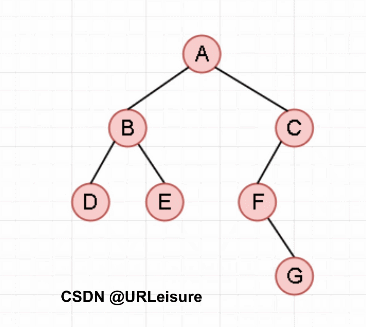
(a gif is 17 pictures + editing + recording. If the watermark is wrong, you have to do it again...)
The c + + code is as follows (example):
void preOrder(Btree T){
if(T){
cout<<T->data<<" ";
preOrder(T->lchild);
preOrder(T->rchild);
}
}
The java code is as follows (example):
public void preOrder(BNode T){
if(T != null){
System.out.print(T.data);
preOrder(T.lchild);
preOrder(T.rchild);
}
}
Middle order traversal
Algorithm steps:
If the binary tree is not empty:
- Traversing the left subtree in middle order;
- Access the root node;
- Traverse the right subtree in middle order.
{first go to the leftmost child, access the node, and then go to the right once; repeat the previous operation (right is empty, this level recursion ends, and returns to the previous level)}
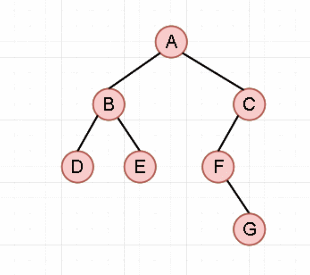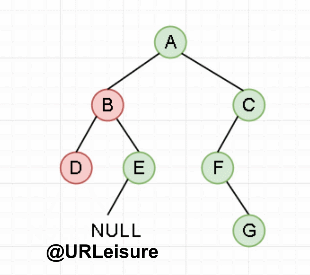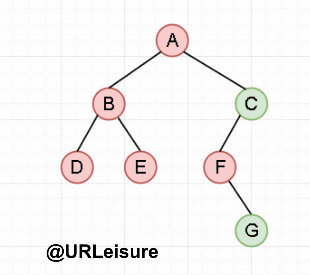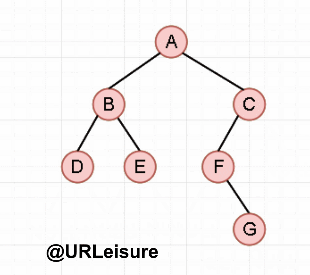
The c + + code is as follows (example):
void inOrder(Btree T){
if(T){
inOrder(T->lchild);
cout<<T->data<<" ";
inOrder(T->rchild);
}
}
The java code is as follows (example):
public void inOrder(BNode T){
if(T != null){
preOrder(T.lchild);
System.out.print(T.data);
preOrder(T.rchild);
}
}
Postorder traversal
Algorithm steps:
If the binary tree is not empty:
- Traversing the left subtree in sequence;
- Traversing the right subtree in order;
- Access the root node.
{go to the leftmost child of the current node first and go to the right once; repeat the previous operation until the right child is empty and access the node (this level recursion ends and returns to the previous level)}
The c + + code is as follows (example):
void postOrder(Btree T){
if(T){
postOrder(T->lchild);
postOrder(T->rchild);
cout<<T->data<<" ";
}
}
The java code is as follows (example):
public void postOrder(BNode T){
if(T != null){
preOrder(T.lchild);
preOrder(T.rchild);
System.out.print(T.data);
}
}
Non recursive code
I found that when reviewing, the most difficult thing is not code, but drawing QAQ.
The interviewer tore the non recursive traversal, which is too "low". (nonsense)
Non recursive generally uses stacks and queues to store.
Use the Standard Template Library (STL) directly, and you can do it.
There are several non recursive writing methods. I feel that I can write different codes from different perspectives.
Two first.
Take the binary tree as an example:

Train of thought 1
Preorder traversal
Our non recursive preorder traversal uses the last in first out feature of stack (stack is implemented with double ended queue in STL).
Algorithm steps:
- Put the root node into the stack;
- Traverse the stack. If the stack is not empty, pop the top node of the stack;
- If the right child of the current pop node is not empty, put the right child into the stack;
- If the left child of the current pop node is not empty, put the left child into the stack.

The c + + code is as follows (example):
void preOrder(Btree T){
if(!T) {//Robust
return;
}
Btree tmp;
stack<Btree> s;
s.push(T);
while(!s.empty()){
tmp = s.top();
s.pop();
cout<<tmp->data<<" ";
if(tmp->rchild){
s.push(tmp->rchild);
}
if(tmp->lchild){
s.push(tmp->lchild);
}
}
}
The java code is as follows (example):
public static void preOrder(BNode T){
if(T == null){
return;
}
BNode tmp;
Stack<BNode> stack = new Stack<>();
stack.push(T);
while(!stack.empty()){
tmp = stack.pop();//java returns out of stack elements, but c + + does not
System.out.print(tmp.data + " ");
if(tmp.rchild != null){
stack.push(tmp.rchild);
}
if(tmp.lchild != null){
stack.push(tmp.lchild);
}
}
}
Middle order traversal
Our non recursive middle order traversal also uses stack to achieve its purpose.
Algorithm steps:
- Set the root node as the latest node and put it into the stack;
- By recursion, all the left children of the latest node are put into the stack;
- pop the last left child, and set the right child of the node as the latest node;
- Then repeat 1 and 2 until the stack is empty.

As can be seen from the figure and the code: there is an empty stack state before entering the stack and after the bottom node is out of the stack, so the termination cannot be judged only by whether the stack is empty or not.
The c + + code is as follows (example):
void inOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s;
Btree tmp,cur = T;
while(!s.empty() || cur){
while(cur){
s.push(cur);
cur = cur->lchild;
}
tmp = s.top();
s.pop();
cout<<tmp->data<<" ";
if(tmp->rchild){
cur = tmp->rchild;
}
}
}
The java code is as follows (example):
public static void inOrder(BNode T){
if(T == null){
return ;
}
BNode tmp,cur = T;
Stack<BNode> stack = new Stack<>();
while(!stack.empty() || cur != null){
while(cur != null){
stack.push(cur);
cur = cur.lchild;
}
tmp = stack.pop();
System.out.print(tmp.data + " ");
if(tmp.rchild != null){
cur = tmp.rchild;
}
}
}
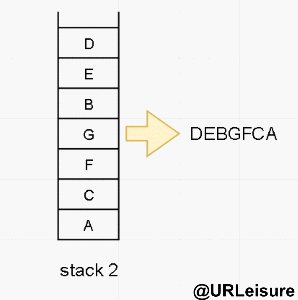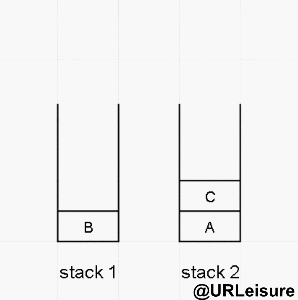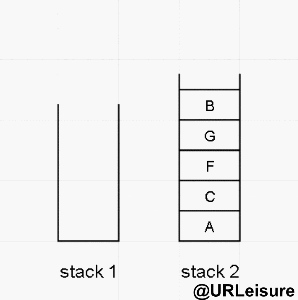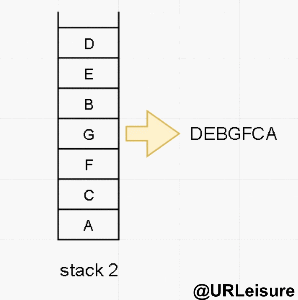
Postorder traversal
Our non recursive post order traversal uses two stacks to achieve its purpose.
Algorithm steps:
- Put the node into stack1, stack1 performs pop operation, and put the pop node into stack2 as the bottom layer;
- Put the left and right nodes of the pop node into stack1 in turn. Put the left node first and then the right node.
- After stack2 is out of the stack, the sequence traversal output results.
The c + + code is as follows (example):
void postOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s1,s2;
Btree p;
s1.push(T);
while(!s1.empty()){
p = s1.top();
s2.push(p);
s1.pop();
if(p->lchild){
s1.push(p->lchild);
}
if(p->rchild){
s1.push(p->rchild);
}
}
while(!s2.empty()){
cout<<s2.top()->data<<" ";
s2.pop();
}
}
The java code is as follows (example):
public static void postOrder(BNode T){
if(T == null){
return ;
}
BNode p;
Stack<BNode> s1 = new Stack<>();
Stack<BNode> s2 = new Stack<>();
s1.push(T);
while(!s1.empty()){
p = s1.pop();
s2.push(p);
if(p.lchild != null){
s1.push(p.lchild);
}
if(p.rchild != null){
s1.push(p.rchild);
}
}
while(!s2.empty()){
System.out.print(s2.pop().data + " ");
}
}
Train of thought II
Personally, I think the second idea is simple and rough, and the recursive idea of direct simulation knocks the code.
All use the stack.
Preorder traversal
The step diagrams are the same.

The c + + code is as follows (example):
void preOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s;
Btree p,cur = T;
while(!s.empty() || cur){
while(cur){
cout<<cur->data<<" ";
s.push(cur);
cur = cur->lchild;
}
p = s.top();
s.pop();
if(p->rchild){
cur = p->rchild;
}
}
}
The java code is as follows (example):
public static void preOrder(BNode T){
if(T == null){
return ;
}
BNode p,cur = T;
Stack<BNode> stack = new Stack<>();
while(!stack.empty() || cur != null){
while(cur != null){
System.out.print(cur.data + " ");
stack.push(cur);
cur = cur.lchild;
}
p = stack.pop();
if(p.rchild != null){
cur = p.rchild;
}
}
}
You can also write:
void preOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s;
Btree p,cur = T;
while(!s.empty() || cur){
if(cur){
cout<<cur->data<<" ";
s.push(cur);
cur = cur->lchild;
}else{
p = s.top();
s.pop();
cur = p->rchild;
}
}
}
Middle order traversal
The step diagrams are the same.

The c + + code is as follows (example):
void inOrder(Btree T){
if(!T){
return false;
}
stack<Btree> s;
Btree p,cur = T;
while(!s.empty() || cur){
while(cur){
s.push(cur);
cur = cur->lchild;
}
p = s.top();
s.pop();
cout<<p->data<<" ";
if(p->rchild){
cur = p->rchild;
}
}
}
The java code is as follows (example):
public static void inOrder(BNode T) {
if (T == null) {
return ;
}
BNode p,cur = T;
Stack<BNode> stack = new Stack<>();
while(!stack.empty() || cur!=null){
while(cur != null) {
stack.push(cur);
cur = cur.lchild;
}
p = stack.pop();
System.out.print(p.data + " ");
if(p.rchild != null){
cur = p.rchild;
}
}
}
You can also write:
void inOrder(Btree T){
if(!T){
return;
}
stack<Btree> s;
Btree p,cur = T;
while(!s.empty() || cur){
if(cur){
s.push(cur);
cur = cur->lchild;
}else{
p = s.top();
s.pop();
cout<<p->data<<" ";
cur = p->rchild;
}
}
}
Postorder traversal
The step diagrams are the same.

The c + + code is as follows (example):
void postOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s;
Btree pre,p,cur = T;
while(!s.empty() || cur){
while(cur){
s.push(cur);
cur = cur->lchild;
}
p = s.top();
s.pop();
if(!p->rchild || p->rchild==pre){//Judge whether this node has or has output right child
cout<<p->data<<" ";
pre = p;
}else {
s.push(p);//p is not the object to be output, and then install it back
cur = p->rchild;
}
}
}
The java code is as follows (example):
public static void postOrder1(BNode T) {
if (T == null) {
return ;
}
BNode p, cur = T;
BNode pre = null;
Stack<BNode> stack = new Stack<>();
while(!stack.isEmpty() || cur!=null){
while(cur != null){
stack.push(cur);
cur = cur.lchild;
}
p = stack.pop();
if(p.rchild==null || p.rchild == pre){
System.out.print(p.data + " ");
pre = p;
}else{
stack.push(p);
cur = p.rchild;
}
}
}
You can also write:
void postOrder(Btree T){
if(!T){
return ;
}
stack<Btree> s;
Btree pre,p,cur = T;
while(!s.empty() || cur){
if(cur){
s.push(cur);
cur = cur->lchild;
}else{
p = s.top();
s.pop();
if(!p->rchild || p->rchild==pre){//Judge whether this node has or has output right child
cout<<p->data<<" ";
pre = p;
}else {
s.push(p);//p is not the object to be output, and then install it back
cur = p->rchild;
}
}
}
}
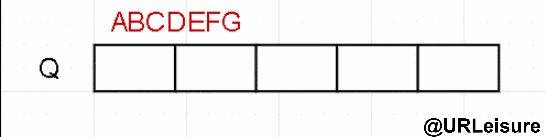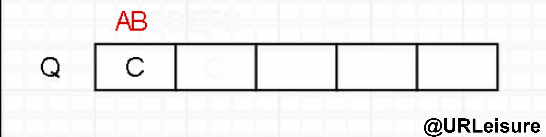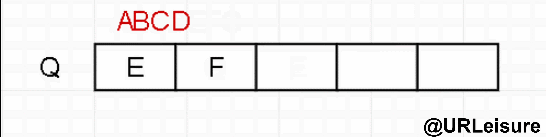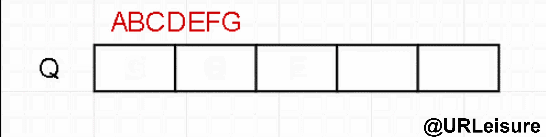
level traversal
The sequence is different from the front, middle and rear, and queues are required.
Algorithm steps:
- Join the team at the node;
- When the team leader element leaves the team, judge whether there are left and right children and join the team in turn.
The c + + code is as follows (example):
bool leveOrder(Btree T){
if(!T){
return false;
}
queue<Btree> q;
Btree p;
q.push(T);
while(!q.empty()){
p = q.front();
cout<<p->data<<" ";
q.pop();
if(p->lchild){
q.push(p->lchild);
}
if(p->rchild){
q.push(p->rchild);
}
}
return true;
}
The java code is as follows (example):
public static void leveOrder(BNode T){
LinkedList<BNode> queue = new LinkedList<>();
BNode p;
queue.add(T);
while(!queue.isEmpty()){
p = queue.pop();
System.out.print(p.data + " ");
if(p.lchild != null){
queue.add(p.lchild);
}
if(p.rchild != null){
queue.add(p.rchild);
}
}
}
summary
Non recursive is very simple. Just do it a few more times.
Next issue Preview: clue binary tree
Update again on February 7, Chinese New Year!!! Wish you a happy new year in advance!!!