Spark recommended combat series has been updated:
- Introduction and implementation of Swing algorithm of Spark recommended practical series and its practical application in Ali flying pig
- Implementation analysis of ALS algorithm of Spark recommended combat series
- How to use matrix operation to indirectly realize i2i in Spark
- Introduction to the principle, Spark implementation and application of FP growth algorithm
- Introduction, experiment and application of Word2vec algorithm in Spark recommended series
For more exciting content, please continue to pay attention to the "search and recommendation Wiki"!
1. Background
Word2vec is a tool for calculating word vectors proposed by Google in 2013. In the paper effective estimation of word representations in vector space, the author proposed word2vec calculation tool, and verified the effectiveness of word2vec by comparing NNLM and RNNLM language models.
The word2vec tool contains two models: CBOW and skip gram. The introduction in the paper is relatively simple, as shown in the figure below. CBOW predicts the central word through the word of context, and skip gram predicts the word of context through the input word.
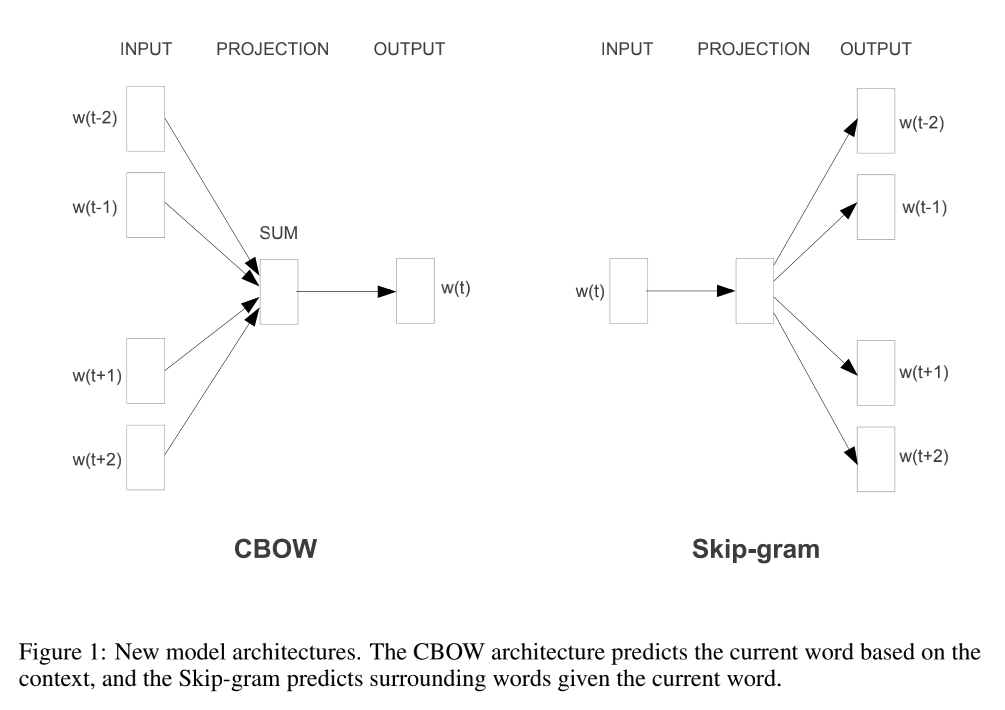
Word2vec started the work related to embedding. Since embedding began to enter the recommendation system on a large scale, let's take a look at the principle, Spark implementation and application description of word2vec algorithm.
2. Algorithm principle
Word2vec includes two models: CBOW and skip gram. CBOW is divided into:
- One-word context
- multi-word context
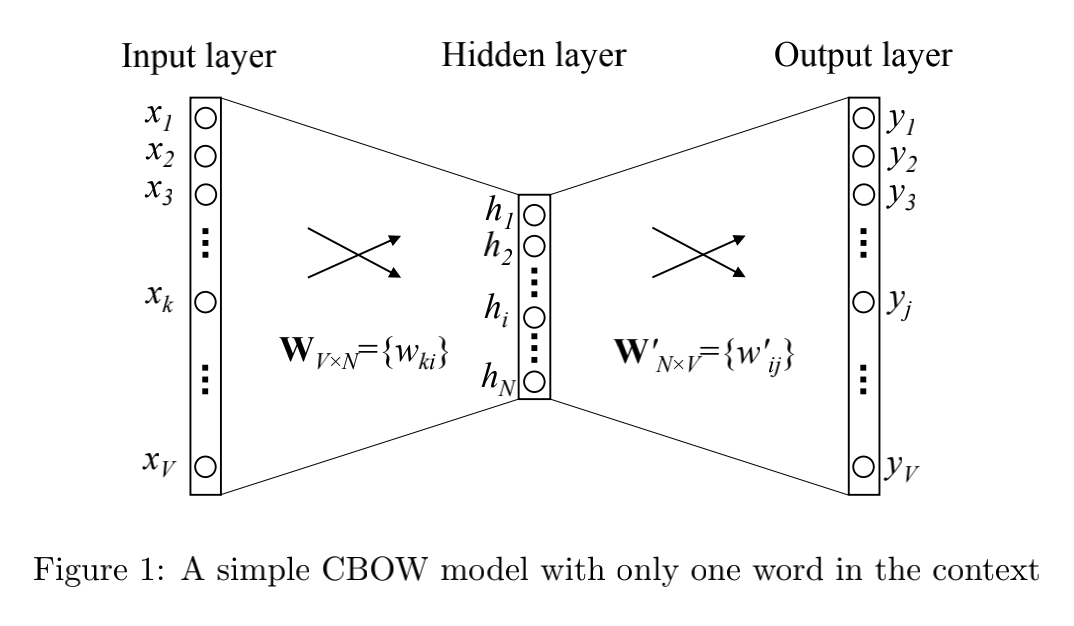
The total number of words is V V 5. The number of neurons in the hidden layer is N N N. The weight matrix from input layer to hidden layer is W V ∗ N W_{V*N} WV * N, the weight matrix from hidden layer to output layer is W N ∗ V ′ W'_{N*V} WN∗V′.
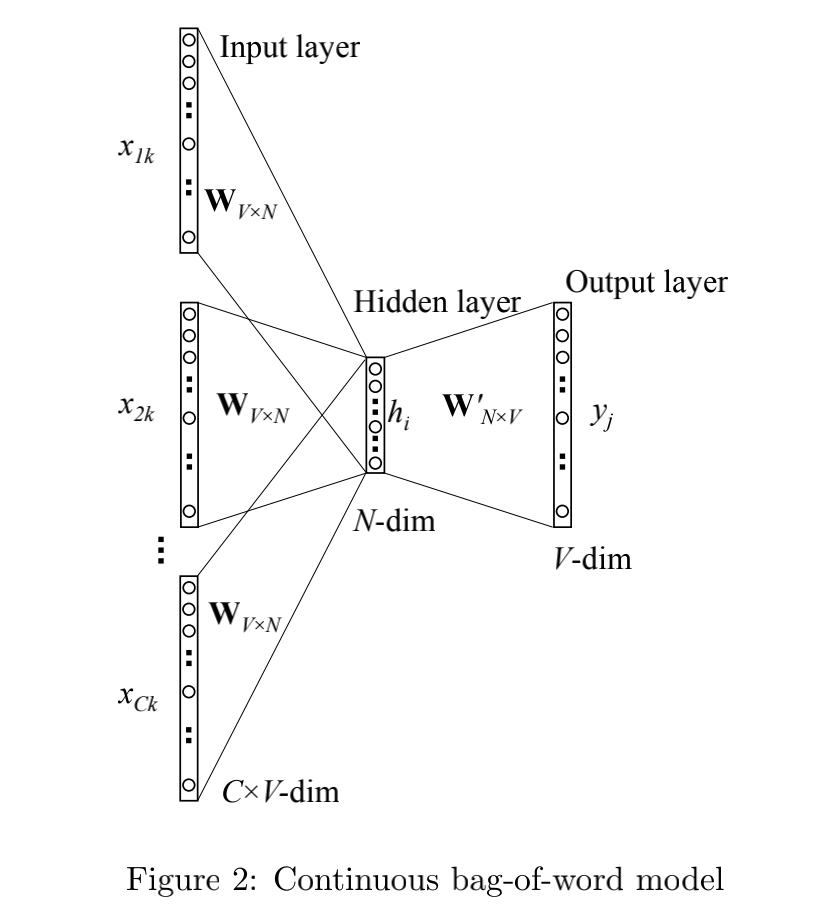
At this time
h
h
The h expression is:
h
=
1
C
W
T
(
x
1
+
x
2
+
.
.
.
.
+
x
C
)
=
1
C
(
v
w
1
+
v
w
2
+
.
.
.
+
v
w
C
)
T
h = \frac{1}{C} W^T (x_1 + x_2 + .... + x_C) \\ = \frac{1}{C} (v_{w_1} + v_{w_2}+ ... + v_{w_C})^T
h=C1WT(x1+x2+....+xC)=C1(vw1+vw2+...+vwC)T
among
C
C
C represents the number of context words,
w
1
,
w
2
,
.
.
.
,
w
C
w_1, w_2, ..., w_C
w1,w2,..., wC , denotes contextual words,
v
w
v_w
vw , represents the input vector of the word (attention and input layer)
x
x
x difference).
The objective function is:
E
=
−
l
o
g
p
(
w
O
∣
w
I
1
,
w
I
2
,
.
.
.
,
w
I
C
)
=
−
u
j
∗
l
o
g
∑
j
′
=
1
V
e
x
p
(
u
j
′
)
=
−
(
v
w
O
′
)
T
∗
h
+
l
o
g
∑
j
′
=
1
V
e
x
p
(
(
v
w
j
′
)
T
∗
h
)
E = -log \, p(w_O | w_{I_1}, w_{I_2}, ..., w_{I_C}) \\ = - u_j * log \sum_{j'=1}^{V} exp(u_j') \\ = -(v'_{w_O})^T * h + log \sum_{j'=1}^{V} exp((v'_{w_j})^T * h)
E=−logp(wO∣wI1,wI2,...,wIC)=−uj∗logj′=1∑Vexp(uj′)=−(vwO′)T∗h+logj′=1∑Vexp((vwj′)T∗h)
The corresponding figure of skip gram is as follows:
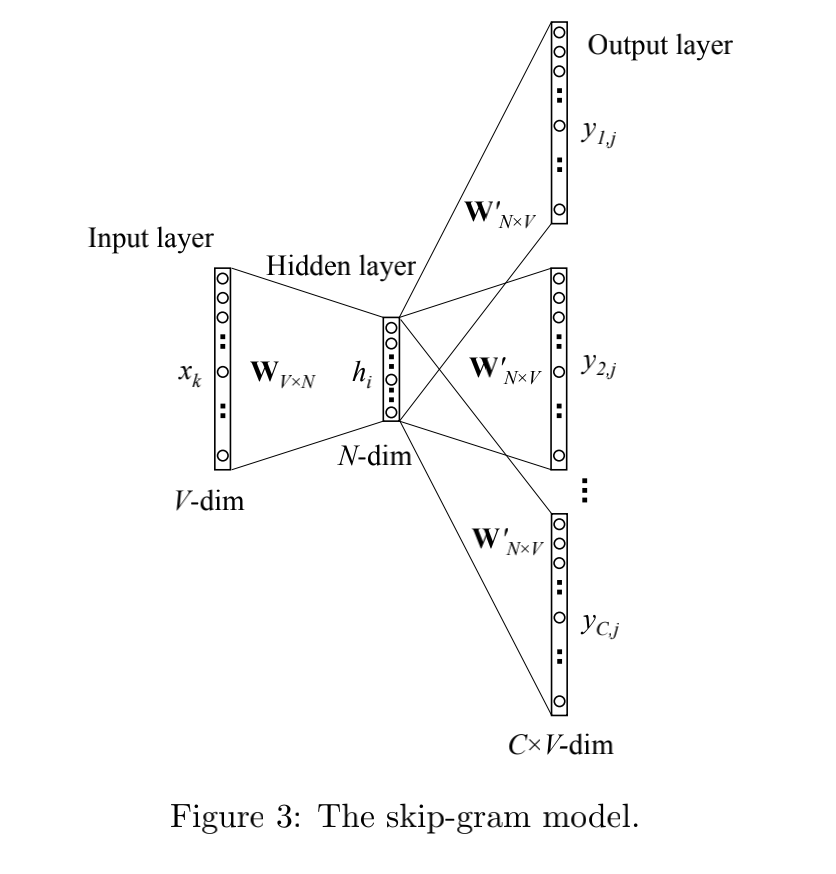
From input layer to hidden layer:
h
=
W
k
,
.
T
:
=
v
w
I
T
h =W^T_{k,.} := v^T_{w_I}
h=Wk,.T:=vwIT
From hidden layer to output layer:
p
(
w
c
,
j
=
w
O
,
c
∣
w
I
)
=
y
c
,
j
=
e
x
p
(
u
c
,
j
)
∑
j
′
=
1
V
e
x
p
(
u
j
′
)
p(w_{c,j}= w_{O,c} | w_I) = y_{c, j} = \frac{exp(u_{c,j})} {\sum_{j'=1}^{V}exp(u_{j'})}
p(wc,j=wO,c∣wI)=yc,j=∑j′=1Vexp(uj′)exp(uc,j)
Of which:
- w I w_I wI , refers to the input word
- w c , j w_{c,j} wc,j , indicates the output layer c c The word c actually falls in the second place j j j neurons
- w O , c w_{O,c} wO,c , indicates the output layer c c The word c should fall in the second place O O O neurons
- y c , j y_{c,j} yc,j , indicates the output layer c c The word c actually falls in the second place j j Normalized probability on j neurons
- u c , j u_{c,j} uc,j , indicates the output layer c c The word c actually falls in the second place j j UN normalized values on j neurons
Because the model training based on word2vec framework requires a very large corpus, so as to ensure the accuracy of the results. However, with the increase of the expected corpus, there is a time-consuming calculation and resource consumption. So is there room for optimization? For example, you can sacrifice certain accuracy to speed up training. The answers are hierarchical softmax and negative sampling.
The paper "distributed representations of words and phases and their composition" introduces two techniques for training word2vec (also explained and explained in detail in the paper "word2vec Parameter Learning Explained"). Let's take a look at them in detail.
We won't expand the description here. Please refer to the previous article: https://mp.weixin.qq.com/s/Yy-mAPOdIEj0u65mxCwzaQ
3.Spark implementation
The encapsulation of word2vec is realized in mllib of spark, which is implemented and applied based on mllib
Main function
def main(args: Array[String]): Unit = {
val spark = SparkSession.builder().master("local[10]").appName("Word2Vec").enableHiveSupport().getOrCreate()
Logger.getRootLogger.setLevel(Level.WARN)
val dataPath = "data/ml-100k/u.data"
val data: RDD[Seq[String]] = spark.sparkContext.textFile(dataPath)
.map(_.split("\t"))
.map(l => (l(0), l(1)))
.groupByKey()
.map(l => l._2.toArray.toSeq)
val word2vec = new Word2Vec()
.setMinCount(minCount)
.setNumPartitions(numPartitions)
.setNumIterations(numIterations)
.setVectorSize(vectorSize)
.setLearningRate(learningRate)
.setSeed(seed)
val model = word2vec.fit(data)
// Output the embedding vector corresponding to item id to
saveItemEmbedding(spark, model)
// Calculate the item similarity using the prevention provided by spark
calItemSim(spark, model)
// Customize cosine similarity to calculate item similarity
calItemSimV2(spark, model)
spark.close()
}
Save item embedding
def saveItemEmbedding(spark: SparkSession, model: Word2VecModel) = {
val normalizer1 = new Normalizer()
val itemVector = spark.sparkContext.parallelize(
model.getVectors.toArray.map(l => (l._1, normalizer1.transform(new DenseVector(l._2.map(_.toDouble)))))
).map(l => (l._1, l._2.toArray.mkString(",")))
println(s"itemVector count: ${itemVector.count()}")
itemVector.take(10).map(l => l._1 + "\t" + l._2).foreach(println)
import spark.implicits._
val itemVectorDF = itemVector.toDF("spuid", "vector")
.select("spuid", "vector")
itemVectorDF.show(10)
// itemVectorDF.write.save("xxxx")
}
Calculate item similarity
def calItemSim(spark: SparkSession, model: Word2VecModel) = {
// This method is compared offline. It seems that using cosine to calculate item similarity is not as good as the latter
val itemsRDD: RDD[String] = spark.sparkContext.parallelize(model.getVectors.keySet.toSeq)
import spark.implicits._
val itemSimItemDF = itemsRDD.map(l => (l, model.findSynonyms(l, 500)))
.flatMap(l => for(one <- l._2) yield (l._1, one._1, one._2) )
.toDF("source_spu", "target_spu", "sim_score")
itemSimItemDF.show(10)
}
def calItemSimV2(spark: SparkSession, model: Word2VecModel) = {
val normalizer1 = new Normalizer()
val itemVector = spark.sparkContext.parallelize(
model.getVectors.toArray.map(l => (l._1, normalizer1.transform(new DenseVector(l._2.map(_.toDouble)))))
).map(l => (l._1, l._2.toArray.toVector))
import spark.implicits._
val itemSimItem = itemVector.cartesian(itemVector)
.map(l => (l._1._1, (l._2._1, calCos(l._1._2, l._2._2))))
.groupByKey()
.map(l => (l._1, l._2.toArray.sortBy(_._2).reverse.slice(0, 500)))
.flatMap(l => for(one <- l._2) yield (l._1, one._1, one._2))
.toDF("source_spu", "target_spu", "sim_score")
itemSimItem.show(10)
}
def calCos(vector1: Vector[Double], vector2: Vector[Double]): Double = {
//Calculate some molecules of the formula
val member = vector1.zip(vector2).map(d => d._1 * d._2).sum
//Find the value of the first variable in the denominator
val temp1 = math.sqrt(vector1.map(num => {
math.pow(num, 2)
}).sum)
//Find the value of the second variable in the denominator
val temp2 = math.sqrt(vector2.map(num => {
math.pow(num, 2)
}).sum)
//Find the denominator
val denominator = temp1 * temp2
//Calculate
member / denominator
}
4. Application
In fact, after Item Embedding is produced, i2i recall or u2i recall can be carried out in the recall stage. The specific usage is described as follows:
- I2i: we can calculate the similar item list of items offline or retrieve i2i through es and faiss in real time, so that u2i & i2i can be recalled online in real time (the general effect of real-time recall is better, as long as the i2i mined is not too outrageous)
- U2i: you can make an avg pooling according to several spu s that the user has recently clicked to get the user's embedding, and then perform similar calculation & retrieval of embedding offline or online to get the recall of u2i
In the sorting stage, the data of item embedding can be used as features, but it should be noted that after the embedding is output, the vector is generally normalized, which is more convenient for the algorithm to use after entering the algorithm
If it is item embedding based on semantic information output, it can also be used in the display mechanism. Its general principle is to avoid too high similarity of adjacent items (refer to MMR algorithm for details)
The premise for word2vec to achieve a good effect is that the system data is relatively rich. For sequences with sparse data, the expression ability of item embedding learned by word2vec is not good.
[technical service] Click to view the details: https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg
Scan and follow the "search and recommendation Wiki"! "Focus on the search and recommendation system, focus on series sharing, and continue to create high-quality content!"