
Coloring is used to judge whether a graph is a bipartite graph
Bipartite graph: all points in the graph can be divided into two sides, so that all edges are between sets, and there are no edges inside the set
Properties used: a graph is a bipartite graph if and only if the graph can be dyadic
A graph is a bipartite graph if and only if it does not contain odd rings. On the contrary, if it is a bipartite graph, it must not contain odd rings
Sufficient proof: since there are no odd rings in the graph, there must be no contradiction in the dyeing process
This sentence can also be proved by the method of counter evidence: if there is a contradiction, it must be that if you dye it from one point, you will find that if you find a point with the same color from one point, you will get that the ring is odd, and if there is a contradiction, it must be odd
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10, M = 2e5 +10;
int e[M], ne[M], h[N], idx;
int color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!color[j])
{
if (!dfs(j, 3 - c)) return 0;
}
else if (color[j] == c) return 0;
}
return 1;
}
signed main()
{
fast;
int n, m;
cin>>n>>m;
// for(int i=0;i<=n;i++) h[i]=-1;
memset(h, -1, (n+1) * sizeof(int));
// memset(h, -1, sizeof h);
int a,b;
// for(int i=0;i<=n;i++) cout<<"i:"<<i<<' '<<h[i]<<endl;
for(int i=1;i<=m;i++)
{
cin>>a>>b;
add(a, b);
add(b, a);
}
bool flag = 1;
for(int i = 1; i <= n; i++)
{
if(!color[i])
{
if(!dfs(i, 1))
{
flag=0;
// cout<<"i:"<<i<<endl;
break;
}
}
}
if(flag) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
hungarian algorithm
A very common algorithm
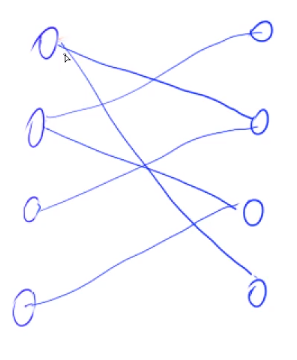
If there is such a graph, the Hungarian algorithm can tell us the maximum number of successful pairings on the left and right sides in the fastest time
Match successful: no two edges share a point
You can think of it this way. There are boys on the left and girls on the right. The side represents favor. Matching is to determine the love relationship and ask how many pairs can be together at most (no cheating)
The idea is to look at boys one by one, first look at the first boy, and then look at which girls he likes each other. Look at girls one by one here. If they are still single, match them first, and then look at the next boy. But if the boy finds that his favorite girl has a boyfriend, the benefits of the Hungarian (dog licking) algorithm come out, He is obsessed. He will see who this girl's boyfriend is, and then see if this girl's boyfriend has other girls who have good feelings. If so, he will give this boyfriend a small goal and ask him to change a girlfriend. If not, give up
Examples
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 510, M = 1e5 +10;
int e[M], ne[M], h[N], idx;
bool st[N];
int match[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
for(int i = h[x]; i!=-1; i = ne[i])
{
int j = e[i];
if(!st[j])
{
st[j] = 1;
if(match[j] == 0 || find(match[j]))
{
match[j] = x;
return 1;
}
}
}
return 0;
}
signed main()
{
fast;
int n1, n2, m;
memset(h, -1, sizeof h);
cin>>n1>>n2>>m;
int a, b;
for(int i=1; i<=m; i++)
{
cin>>a>>b;
add(a, b);
}
int res =0;
for(int i=1;i<=n1;i++)
{
memset(st, 0, sizeof st);
if(find(i)) res++;
}
cout<<res<<endl;
return 0;
}
