7-1 depth first search I (100 points)

Undirected graph G has n vertices and m edges. Find the depth first search tree (forest) of graph G and the discovery time and completion time of each vertex. Each connected component is searched from the node with the smallest number, and the selection order of adjacent vertices follows the input order of edges.

When a node is encountered for the first time in the search process, it is said that the node is found; All adjacent nodes of a node are searched, and the search of the node is completed. Depth first search maintains a clock. The clock counts from 0. When the node is found or completed, the clock count is increased by 1, and then the time stamp is stamped for the current node. The timestamp of a node being found and completed by search is called the discovery time and completion time of the node respectively

input

In the first line, two integers n and m, separated by spaces, represent the number of vertices and edges respectively, 1 ≤ n ≤ 50000, 1 ≤ m ≤ 100000

Lines 2 to m+1, two integers u and V in each line, separated by spaces, indicate that there is an edge from vertex u to vertex v, u and V are vertex numbers, 1 ≤ u,v ≤ n

output

Lines 1 to N, two integers di and fi in each line, separated by spaces, represent the discovery time and completion time of the ith vertex 1 ≤ i ≤ n.

Line n+1, an integer k, represents the number of edges of the depth first search tree (forest) of the graph.

Lines n+2 to n+k+1, with two integers u and v in each line, represent an edge < u, v > of the depth first search tree (forest), and the output order of the edges is numbered from small to large according to the number of v nodes.

sample input

6 5
1 3
1 2
2 3
4 5
5 6

output

1 6
3 4
2 5
7 12
8 11
9 10
4
3 2
1 3
4 5
5 6

Later:

1. The essence of this problem is a DFS deep search, with a timestamp similar to the tarjan () algorithm. The sum of the recursive entry and exit is assigned and one is added. Before the recursive entry, the pass is added to the priority queue and the passing edge is output.
2. Example 4 and example 5: super memory storage mode reason:
(1) Linked list storage graph will lead to the priority queue with storage edge, which will lead to memory overrun. Example 4 and example 5 save images take up half of the storage space.
(2). Use the chained backward star (the forward star is the same as the adjacent linked list + de recursive dfs, and the access order cannot be guaranteed) the memory will not exceed the limit.
(3) Unsolved problems: at present, there are three methods of graph, 1 Adjacency matrix (space complexity O (n^2) 2 Adjacency matrix, according to most blogs I have read, this kind of graph storage is considered to be a method with the smallest time complexity and space complexity. (3) chain forward star, a more moderate method, which has the advantage of simple writing. Therefore, in this problem, there are opposite experimental results for the comparison of spatial complexity between adjacent linked list and linked forward star. The cause remains unresolved.
After commenting out the dfs steps, the memory is used, most of which is spent on drawing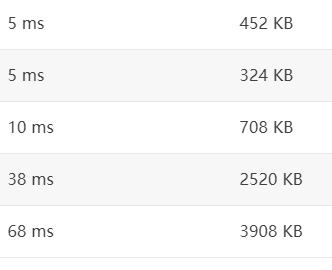
Figure 1: chain forward star

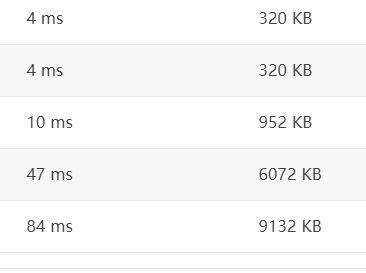
Figure 2 Adjacency List

code

#include<bits/stdc++.h>
using namespace std;
const int maxn = 500005;//Maximum number of points
int n, m, cnt;//n points, m edges
typedef struct Edge
{
    int u,to, w, next;//End point, edge weight, number of the previous edge at the same starting point
} Edge;
Edge edge[2*maxn];//Edge set
int head[maxn];//head[i], indicating the position (number) of the first edge starting from I in the edge set array
void init()//initialization
{
    for (int i = 0; i <= n; i++) head[i] = -1;
    cnt = 0;
}
void add_edge(int u, int v, int w)//Edge addition, u starting point, v ending point, w edge weight
{
	edge[cnt].u=u;
    edge[cnt].to = v; //End
    edge[cnt].w = w; //Weight 
    edge[cnt].next =-1;
    int num=head[u];
    if(head[u]!=-1)
	{
		while(edge[num].next!=-1) num=edge[num].next;
		edge[num].next=cnt;
	}
    else 
	{
    	head[u] = cnt;//Updates the number of the previous edge starting with u
	}
    cnt++;
}
struct cmp {
	bool operator()(Edge a, Edge b)
	{
		return a.to > b.to;
	}
};
priority_queue<Edge, vector<Edge>, cmp> ee;
int times[50001], timee[50001],tt;
void DFS(int v, int u)
{
	tt++;
	times[v] = tt;
	for (int j = head[v]; j != -1; j = edge[j].next)
	{
		if (!times[edge[j].to])
		{
			DFS(edge[j].to, v);
			ee.push(edge[j]);
		}
	}
	timee[v] =++tt;
}
int main()
{
    cin >> n >> m;
    int u, v, w=0;
    init();//initialization
    for (int i = 1; i <= m; i++)//Enter m edges
    {
        cin >> u >> v ;
        add_edge(u, v, w);
        add_edge(v, u, w);
    }
    for(int i=1;i<=n;i++)
    {
    	if(!times[i]) DFS(i,0);
	}
	for (int i = 1; i <= n; i++)
	{
		printf("%d %d\n", times[i], timee[i]);
	}
	int num = ee.size();
	cout<<num<<"\n";
	for (int i = 1; i <= num; i++)
	{
		cout<< ee.top().u<<" "<<ee.top().to;
		ee.pop();
		if (i != num) cout<<"\n";	
	}
    return 0;
}

7-2 circles (100 points)

There are n circles on the two-dimensional plane. Please count the number of different blocks formed by these circles.

The block formed by a circle is defined as follows: (1) a circle is a block; (2) If two blocks have common parts (including tangency), the two blocks form a new block, otherwise they are still two different blocks

Input format

The first line includes an integer n, indicating the number of circles, n < = 8000.

Lines 2 to n+1, each with three numbers x, y, r separated by spaces. (x, y) is the center coordinate and r is the radius. All coordinates and radii are non negative integers no greater than 30000.

Output format

An integer representing the number of blocks formed

sample input

2
0 0 1
1 0 2

sample output

1

Idea:

1. The essence of this problem is to find the connected component of the graph, but the graph is not explicitly given, but a potential and unique graph. The specific method can be realized by using parallel search set.
2. Note that the squared sqrt() function may cause loss of accuracy.

#include <stdio.h>
#include <algorithm>
#include <iostream> 
#include <vector>
#include <math.h>
using namespace std;

typedef struct vertex {
	int x,y,r;
	struct edge* next;
}vertex;
typedef struct graph {
	int vv, ee;
	vector<vertex> verlist;
}graph;
graph* g = new graph;

int father[100000];
int FIND(int x)
{
	while (father[x] >0) x = father[x];
	return x;
}
void UNION(int x, int y)
{
	int fx = FIND(x), fy = FIND(y);
	if (fx == fy) return;
	if (father[fx] < father[fy]) father[fy] = fx;
	else {
		if (father[fx] == father[fy]) father[fy]--;
		father[fx] = fy;
	}
}

int main()
{
	scanf("%d",&g->vv);
	int num=g->vv;
	g->ee = 0;
	for (int i = 0; i < g->vv; i++)
	{
		int x, y,r;
		vertex* p = new vertex;
		cin >> x >> y>>r;
		p->x= x;
		p->y=y;
        p->r=r;
		g->verlist.push_back(*p);

	}
	for (int i = 1,k=0; i <= num; i++)
	{
		for (int j = i + 1; j <= num; j++)
		{
			if (FIND(i) != FIND(j))
			if(sqrt((g->verlist[i-1].x - g->verlist[j-1].x)*(g->verlist[i-1].x - g->verlist[j-1].x) + (g->verlist[i-1].y - g->verlist[j-1].y)*(g->verlist[i-1].y - g->verlist[j-1].y))<=g->verlist[i-1].r+g->verlist[j-1].r)
			{
				UNION(i, j);
				g->vv--;
			}
		}
	}	
	printf("%d",g->vv);
	return 0;
}

7-3 power supply (100 points)

Supply power to N regions. Each area may build a power supply station or build a line to connect to other areas with electricity. Try to determine the minimum cost of supplying power to N regions.

Input sample:

In the first line, two integers N and M, separated by spaces, represent the number of regions and the number of schemes for line repair respectively, 1 ≤ N ≤ 10000, 0 ≤ M ≤ 50000.

The second line contains N integers P[i] separated by spaces, indicating the cost of building a power supply station in the ith area, 1 ≤ P[i] ≤ 100000, 1 ≤ I ≤ N.

The next M lines are 3 integers a,b and c in each line, separated by spaces, indicating that the cost of building a line between areas a and b is c, 1 ≤ c ≤ 100000, 1 ≤ a,b ≤ N.

Output format

A line containing an integer representing the minimum cost.

sample input

4 6
5 4 4 3
1 2 2
1 3 2
1 4 2
2 3 3
2 4 3
3 4 4

sample output

9

analysis

1. The basis of this problem is the minimum spanning tree, but when applied to practice, there will be a special case: the cost of establishing a power station at a certain point is less than the cost of repairing the line. Under the constraints of this special case, kruskal algorithm is difficult to deal with, so prim algorithm is selected to represent the cost of establishing power plant at its own place by adding an anti side.

code

#include <stdio.h>
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
 
using namespace std;

typedef struct edge {
	int ii;
	int cost;
	struct edge* next;
}  edge;
typedef struct vertex {
	int ii;
	int cost;
	struct edge* next;
}vertex;
typedef struct graph {
	int vv, ee;
	vector<vertex> verlist;
}graph;
graph* g = new graph;

int vex[100005], lc[100005], mark[10005];
int cost[100005];
void Prim(int s)
{
	for (int i = 1; i <=g->vv; i++)
	{
		lc[i] = cost[i];
		mark[i] = 0;
	}
	for (int i = 1; i <=g->vv; i++)
	{
		int lw = 1000005, v;
		for (int i = 1; i <= g->vv; i++)
		{
			if (!mark[i] && lw > lc[i])
			{
				lw = lc[i];
				v = i;
			}
		}
		mark[v] = 1;
		edge* p = g->verlist[v-1].next;
		for (p; p; p = p->next)
		{
			if (p->cost < lc[p->ii] && !mark[p->ii])
			{
				lc[p->ii] = p->cost;
			}
		}
	}
}

int min_cost1=100000;
int main()
{
	scanf("%d%d", &g->vv, &g->ee);
	for (int i = 1; i <= g->vv; i++)
	{
		vertex* p = new vertex;
		p->ii = i ;
		p->next = NULL;
		g->verlist.push_back(*p);
	}
	for (int i  = 1; i <= g->vv; i++)
	{
		scanf("%d", &cost[i]);
		if(min_cost1>cost[i]) min_cost1=cost[i]; 
 	}
 	for (int i = 0; i < g->ee; i++)
	{
		int m, n,cost;
		cin >> m >> n>>cost; 
		edge* q = new edge;
		q->ii = n;
		q->cost = cost;
		q->next = NULL;
		if (!g->verlist[m-1].next)
		{
			g->verlist[m-1].next = q;
		}
		else
		{
			edge* head = g->verlist[m-1].next;
			while (head->next)
			{
				head = head->next;
			}
			head->next = q;
		}
		q = new edge;
		q->ii = m;
		q->cost = cost;
		q->next = NULL;
		if (!g->verlist[n-1].next)
		{
			g->verlist[n-1].next = q;
		}
		else
		{
			edge* head = g->verlist[n-1].next;
			while (head->next)
			{
				head = head->next;
			}
			head->next = q;
		}
	}
	int num=0;long long all_cost=0;
	for(int i=1;i<=g->vv;i++)
	{
		if(!mark[i]) 
		{
			Prim(i);num++;
		}
	} 
	for(int i=1;i<=g->vv;i++) all_cost+=lc[i];
	cout<<all_cost; 
}

7-4 red envelopes (100 points)

When the new year comes, the company will send red envelopes to employees. Employees will compare the amount of red envelopes they receive. Some employees will ask for the amount of money. For example, the amount of red envelopes in c1 is more than that in c2. The amount of red envelope money for each employee should be at least 888 yuan, which is a lucky number.

The company wants to meet the requirements of all employees and spend the least money at the same time. Please help calculate.

Input format

In line 1, two integers n and m (n < = 10000, m < = 20000), separated by spaces, represent the number of employees and the required number respectively.

The next m lines are two integers c1 and c2, separated by spaces, indicating that the number of red envelopes of employee c1 is more than c2, and the employee number is 1~n.

Output format

An integer that represents the minimum amount of money the company sends. If the company cannot meet the needs of all employees, output - 1

sample input

2 1
1 2

sample output

1777

analysis:

1. The basic idea of this topic is topological sorting. The salary of the last person out of the team pointed by each person + 1 is his salary, and the failure represents a ring in the pointing diagram.

code

#include <stdio.h>
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
typedef struct edge {
	int ii;
	int cost;
	struct edge* next;
}  edge;
typedef struct vertex {
	int ii;
	int money;
	struct edge* next;
}vertex;
typedef struct graph {
	int vv, ee;
	vector<vertex> verlist;
}graph;
graph* g = new graph;

struct cmp{
	bool operator()(int a,int b)
	{
		return a>b;
	}
};
long long sum;
int count[10005];//Number of nodes 
stack<int> tt;
void tope()
{
	for (int i = 1; i <=g->vv; i++)
		count[i] = 0;
	for (int i = 0; i < g->vv; i++)
	{
		edge* p;
		p = g->verlist[i].next;
		for (p; p; p = p->next)
		{
			count[p->ii]++;
		}
	}
	
	for (int i = 1; i <= g->vv; i++) 
		if (count[i]==0) 
		{
			tt.push(i);
			g->verlist[i-1].money=888;
		}
	for(int i=1;i<=g->vv;i++)
	{
		if(tt.empty()) 
		{
			printf("-1");
			return ; 
		}
		 
		int v = tt.top();
		tt.pop();
		sum+=g->verlist[v-1].money; 
		for (edge* p = g->verlist[v-1].next; p; p = p->next)
		{
			count[p->ii]--;
			if (count[p->ii] == 0) 
			{
				g->verlist[p->ii-1].money=g->verlist[v-1].money+1;
				tt.push(p->ii); 	
			}	 
		}
	}
	printf("%lld",sum); 
}
int main()
{
	scanf("%d%d",&g->vv,&g->ee); 
	for (int i = 1; i <= g->vv; i++)
	{
		vertex* p = new vertex;
		p->ii = i ;
		p->next = NULL;
		g->verlist.push_back(*p);
	}
	for (int i = 0; i < g->ee; i++)
	{
		int m, n;
		scanf("%d%d",&n,&m);
		edge* q = new edge;
		q->ii = n;
		q->cost = 0;
		q->next = NULL;
		if (!g->verlist[m-1].next)
		{
			g->verlist[m-1].next = q;
		}
		else
		{
			edge* head = g->verlist[m-1].next;
			while (head->next)
			{
				if(head->ii==n) break;
				head = head->next;
			}
			if(head->ii!=n) head->next = q; 	
		}
	}
	tope();
}