64 days from the Blue Bridge Cup, let's prepare for the blue bridge cup with Xiao Zheng

Blue Bridge Cup real title link : numeric triangle

        Leedcode frog jumping steps

        Leedcode different paths

I hereby thank the author for his on-demand broadcast, and Xiao Zheng has benefited a lot from it Article sourcehttps://cloud.tencent.com/developer/article/1538177

Frog jumping steps:(introductory question)

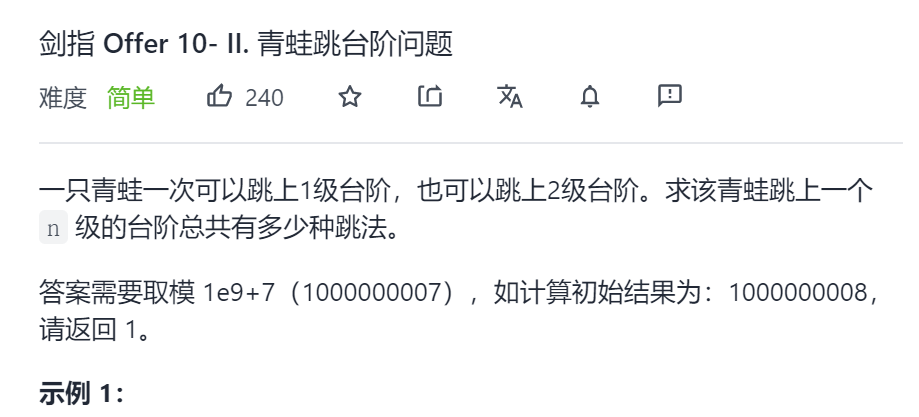
Simple idea: see the code for analysis (although the recursion timeout, the idea is worth learning)

class Solution:
    def numWays(self, n: int) -> int:
        #dp[n] stands for jumping up the nth step. There are dp[n] jumping methods
        #Find recurrence relation dp[n]=dp[n-1]+dp[n-2]
        #Initial value dp[0]=1,dp[1]=1,dp[2]=2
        searched=[1,1,2]
        if n==0:
            return 1
        elif n==1:
            return 1
        elif n==2:
            return 2
        else:
            return self.numWays(n-1)+self.numWays(n-2)

In fact, if you look closely at the Fibonacci sequence, it's easy to do 😀

class Solution:
    def numWays(self, n: int) -> int:
        a,b=1,1
        for i in range(n-1):
            a,b=(a+b)%1000000007,a%1000000007
        return a

Some details of the second set of code are described below. This problem only emphasizes the idea of dynamic programming: defining array meaning + recursive relationship + benchmark value
https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/solution/mian-shi-ti-10-ii-qing-wa-tiao-tai-jie-wen-ti-dong/

 

Different paths: (Advanced questions)

Code design idea:

1: Definition of array meaning: dp[i][j]: there are dp[i][j] methods from row I to column j

2: Looking for recurrence relation: similar to frog jumping steps. Because it can only go down or right, any grid except the grid in the first column and the first row jumps from the upper grid or the grid on the left. Therefore, by analogy with the first question, we can get the recurrence relation: dp[i][j]=dp[i-1][j]+dp[i][j-1]

3: Initial value setting: from 2, we need to define DP [i] [0] (0 < = I < = m-1) and dp[0][j] (0 < = J-1 < = n) as 1

Let's make all dp[i][j] 1, because in any case, except dp in the first row or column, the value should be updated through recursive relationship

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[[1]*n for i in range(m)]
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]

Blue Bridge Cup real problem analysis: Digital triangle (AC)

Code design analysis:

Array definition: dp[i][j] represents the maximum path of row I and column j, because it can only move left and right (a[i][j] represents the number of row I and column j)
Therefore, the recurrence relation: dp[i][j]=max(dp[i-1][j]+dp[i-1][j-1])+a[i][j]

The initial value column 0 and row i can only be obtained by moving the column 0 and row i-1 left, so the prefix and

path[i][j] records the left and right moving paths, which are related to the path of the upper layer. We define left-1 and right + 1

Every element of the rightmost column of the original triangle can be seen as the number in the upper left corner plus 0

Therefore, we fill a[i][j] with 0} code as follows:

n=int(input())
a=[]

for _ in range(n):
    tmp=list(map(int,input().split()))
    tmp+=[0]*(n-len(tmp))
    a.append(tmp)

dp=[[0]*n for i in range(n)]
path=[[0]*n for i in range(n)]#Record the left-right path left-1 right + 1

dp[0][0]=a[0][0]
for i in range(1,n):
    dp[i][0]=dp[i-1][0]+a[i][0]#initial value
    path[i][0]=path[i-1][0]-1
    

for i in range(1,n):
    for j in range(1,n):
        #dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j]
        if dp[i-1][j]>=dp[i-1][j-1]:#Turn left from the upper floor
            dp[i][j]=dp[i-1][j]+a[i][j]
            path[i][j]=path[i-1][j]-1
        else:
            dp[i][j]=dp[i-1][j-1]+a[i][j]
            path[i][j]=path[i-1][j-1]+1

ans=0
for k in range(0,n):
    if abs(path[-1][k])<=1:
        ans=max(ans,dp[-1][k])
print(ans)

 I am Xiao Zheng, looking forward to working with you to love! Blue bridge impact!