Before learning about queen 2n, we should know the queen n problem:

N queens are placed on the N*N checkerboard so that they do not attack each other (that is, any two queens are not allowed to be in the same row, the same column, or on the slash at a 45 angle with the checkerboard border).
Your task is to find out how many legal placement methods there are for a given N.
Input sample:
1
8
5
0
Output example:
1
92
10

It can be understood that taking queen 4 as an example:

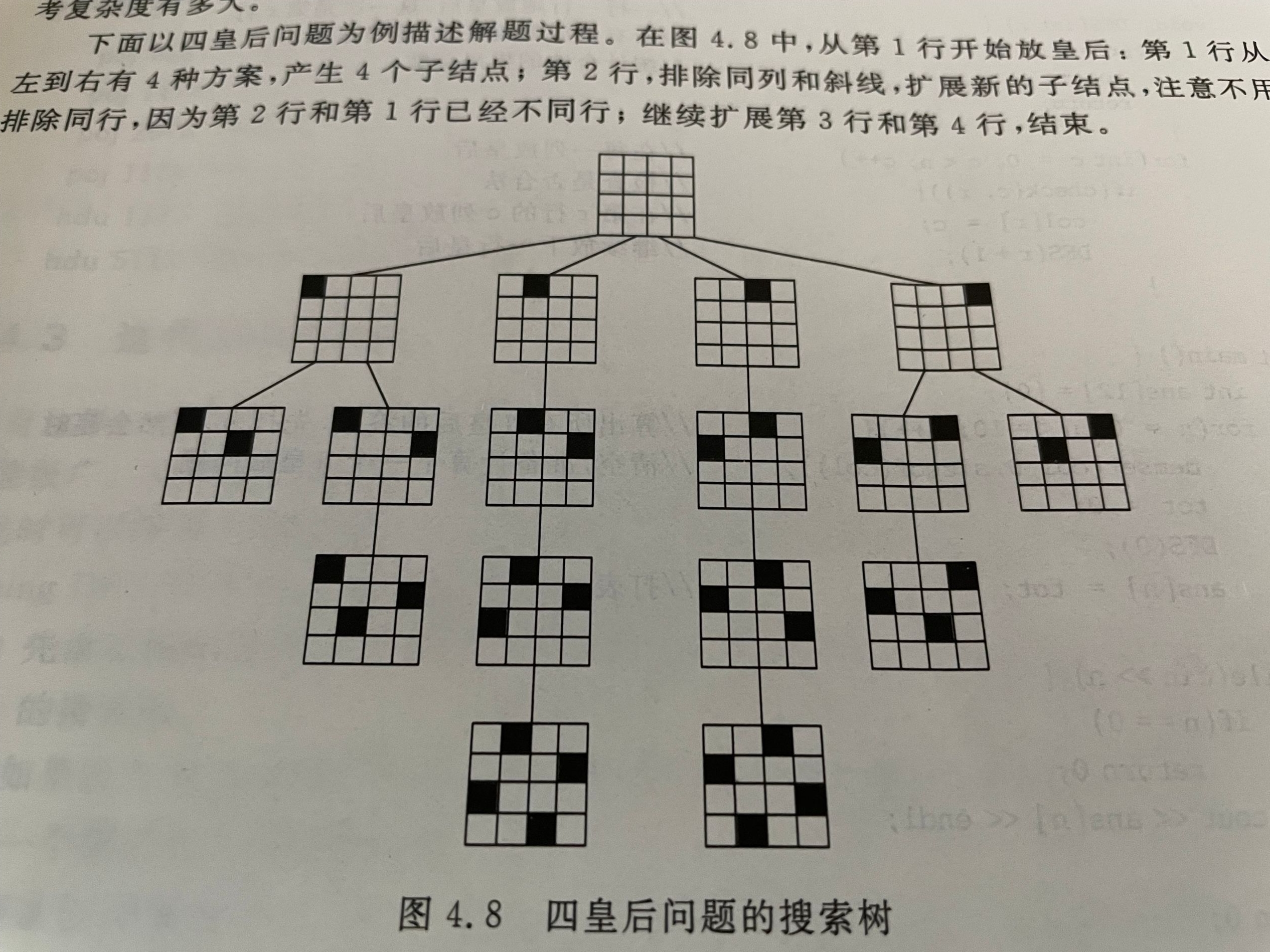
Now the remaining problem is to make the algorithm more efficient through some necessary operations, which is pruning;

It can be considered that the coordinates of the queen in the first row and the first column are (0, 0), and the coordinates of the queen are (i,j). In order to avoid repetition, the coordinates of the new queen are (r,c),

You can see: in order to avoid the same column J= c；

Then we don't need to compare our peers (because we follow the principle of placing only one queen in each line);

If you take a step obliquely from the coordinates of the queen to the coordinates of the new queen, then there are the coordinates of the new queen. Relative to the coordinates of the queen, there are upper left (i-r,j-c), lower left (i-a,j+a), lower right (i+a,j+a) and upper right (i+a,j-a). In any case, it is | i-r|=|j-c|;

In order to meet the requirements of the topic, there is | i-r |=| j-c|；

The title is clear, and the code is as follows:

#include<bits/stdc++.h>
using namespace std;
int col[12]={0};  //col The array is used to store the second row i Line number col[i]Column to place the queen.
int n,tot = 0;        //Set the global variable to call directly without setting the value
bool check(int r,int c){        //Judge whether the new queen conflicts with the placed queen.
    for(int i=0;i<r;i++){
        //You don't need to judge whether you are in the same row here, because we only put one queen in each row, so you don't need to judge, just judge whether it is the same column or the same slash.
        if((col[i]==c)||(abs(col[i]-c)==abs(i-r)))return false;
    }
    return true;
}
void dfs(int r){
    if(r==n){ //Because starting from 0, the number of rows r achieve n When, it means that it has been completed
        tot++;
        return ;
    }
    for(int c=0;c<n;c++){
        if(check(r,c)){ //Judge whether it can be placed, it can be placed, otherwise prune.
            col[r]=c;
            dfs(r+1);    //Continue to place the new queen on the next line
        }
    }
}
int main(){
    int ans[12]={0};
    for(n=0;n<=10;n++){             //yes n The queen types the table and stores the results ans array
        memset(col,0,sizeof(col));     //Initialize each time
        tot=0;
        dfs(0);                    //DFS
        ans[n]=tot;                //deposit
    }
    while(cin >> n){
        if(n==0)return 0;
        cout << ans[n] << endl;
    }
    return 0;
}

And attach a good video link: https://www.bilibili.com/video/BV1bK4y1n7iq?spm_id_from=333.999.0.0

The next step is queen 2n. The general idea is similar to that of Queen n. The difference is that we need to judge whether we can release the queen. We can solve it as follows:

After releasing the black queen (first release the black queen), we are dealing with the White Queen. If not, we should judge whether we can release the queen. Then for the white queen, we should judge whether the position is occupied by the black queen while judging whether we can release the queen

The code is as follows:

#include<bits/stdc++.h>
using namespace std;
const int maxn = 10;  
int n;  
int mapqueen[maxn][maxn];  //Can you let the queen go 
int whqueen[maxn]={0};  //White Queen position 
int blqueen[maxn]={0};  //Black queen position 
int ans; 
bool checkbl(int step,int c)
{
    for(int i=1;i<step;i++)
    {
        if(blqueen[i]==c||(abs(blqueen[i]-c)==abs(i-step)))
        return false;
    }
    return true;
}
bool checkwh(int step,int c)
{
    for(int i=1;i<step;i++)
    {
        if(whqueen[i]==c||(abs(whqueen[i]-c)==abs(i-step)))
        return false;
    }
    return true;
}
void dfs_white(int step)
{
    if(step==n+1)
    {
        ans++;
    }
    for(int c=1;c<=n;c++)
    {
        if(blqueen[step]==c)
        continue;
        if(mapqueen[step][c]==0)
        continue;
        whqueen[step]=c;
        if(checkwh(step,c))
        {
            dfs_white(step+1); 
        }
    }
}
void dfs_black(int step)
{
    if(step==n+1)
    {
        dfs_white(1);
    }
    for(int c=1;c<=n;c++)
    {
        if(mapqueen[step][c]==0)//The first step Line number i Whether the conditions for the queen are listed 
        continue;
        blqueen[step]=c;//In the first step Line i Lie Fang black queen
        if(checkbl(step,c))
        {
            dfs_black(step+1);//Go to the next floor 
         } 
    }
 } 
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            scanf("%d",&mapqueen[i][j]);
        }
    }
    dfs_black(1);//Search the black queen from the first line 
    printf("%d\n",ans); 
    return 0;
}