1. Title

Give you an integer array nums, in which the elements have been arranged in ascending order. Please convert it into a highly balanced binary search tree.

A height balanced binary tree is a tree that satisfies the requirement that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1 1 1」 Binary tree.

1.1 example

• Examples 1 1 1 :

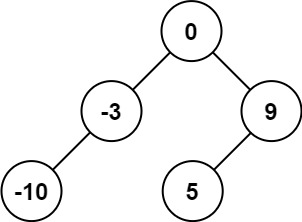
  • Input: root = [-10, -3, 0, 5, 9];

  • Output: [0, -3, 9, -10, null, 5];

  • **Explanation: * * a possible answer is: [0, -3, 9, -10, null, 5], which can represent the following highly balanced binary search tree.

• Examples 2 2 2 :

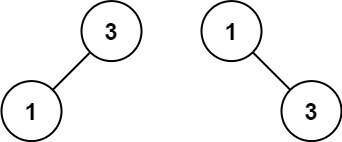
  • Input: root = [1, 3];

  • Output: [3, 1];

  • Explanation: [1,3] and [3,1] are highly balanced binary search trees.

1.2 description

• Source: LeetCode
• Link: https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree

1.3 restrictions

• The number of nodes in the given linked list ranges from [ 0 ,   2 ∗ 1 0 4 ] [0,\text{ }2 * 10^4] [0, 2∗104] ；
• − 1 0 5 ≤ Node.val ≤ 1 0 5 -10^5 \le \text{Node.val} \le 10^5 −105≤Node.val≤105

2. Solution I

2.1 analysis

Because the middle order traversal of the binary search tree will get an ascending sequence, the ascending sequence can be regarded as the middle order traversal result of the binary search tree, and then the binary search tree can be constructed.

Generally speaking, the construction of binary tree (binary search tree is a special binary tree) usually uses the recursive method, that is, first build the root node, and then recursively build the left and right subtrees. Therefore, the most important thing is how to determine the elements corresponding to the root node according to the given sequence, and then further determine the elements corresponding to the left and right subtree nodes.

Unfortunately, in general, it is impossible to directly construct the original binary tree only through a certain traversal sequence of the binary tree, because at least the two traversal sequences of the binary tree need to be combined to determine the elements corresponding to the root node and the elements corresponding to the left and right subtrees, which is why LeetCode The first 105 105 105 questions and The first 106 106 106 questions The sequences obtained by two kinds of traversal of binary tree are given respectively.

Fortunately, the binary search tree required by this problem is balanced, that is, the absolute value of the height difference between the left and right subtrees of each node does not exceed 1 1 1, then it can be considered that the elements of the root node correspond to the intermediate elements of the ordered sequence, and the left side of the intermediate element is the element sequence of all nodes of the left subtree, and the right side of the intermediate element is the element sequence of all nodes of the right subtree.

According to the above analysis, it can actually be imitated [LeetCode binary tree project] maximum binary tree (654) The following recursive solution is given:

2.2 answers

from collections import deque
from typing import List, Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def sorted_array_to_bst(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums:
            return
        length = len(nums)
        root_idx = length // 2
        root = TreeNode(nums[root_idx])
        root.left = self.sorted_array_to_bst(nums[:root_idx])
        root.right = self.sorted_array_to_bst(nums[root_idx + 1:])
        return root


def main():
    nums = [-10, -3, 0, 5, 9]
    sln = Solution()
    root = sln.sorted_array_to_bst(nums)

    tree = []
    visiting = deque([root])
    while visiting:
        node = visiting.popleft()
        if node:
            tree.append(node.val)
            visiting.append(node.left)
            visiting.append(node.right)
        else:
            tree.append(None)

    while True:
        if not tree[-1]:
            tree.pop()
        else:
            break

    print(tree)  # [0, -3, 9, -10, None, 5]


if __name__ == '__main__':
    main()

It should be noted that since Python's slicing syntax is closed on the left and open on the right, the above code uses num [: root_idx] instead of [: root_idx - 1] when building the left subtree recursively.

2.3 complexity

• Time complexity: O ( n ) O(n) O(n) .

2.4 code optimization

In fact, the above solution uses Python's list slicing syntax every time it recurses, and the syntax allocates new memory space every time it is executed. Therefore, the space complexity of the above solution is high. This can be optimized as follows:

from typing import List, Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def _array2bst(self, nums: List[int], start: int, stop: int) -> Optional[TreeNode]:
        if start > stop:
            return
        root_idx = start + (stop - start) // 2
        root = TreeNode(nums[root_idx])
        root.left = self._array2bst(nums, start, root_idx - 1)
        root.right = self._array2bst(nums, root_idx + 1, stop)
        return root

    def sorted_array_to_bst(self, nums: List[int]) -> Optional[TreeNode]:
        return self._array2bst(nums, 0, len(nums) - 1)

The time complexity of the above implementation remains unchanged, while the space complexity is O ( log  n ) O(\text{log }n) O(log n), where n n n is the length of the array. The spatial complexity does not consider the return value, so the spatial complexity mainly depends on the depth of the recursive stack, which is O ( log ⁡ n ) O(\log n) O(logn) .