High Precision Addition, Subtraction, Multiplication and Division Algorithms

What is high precision?

High Accuracy Algorithm s are mathematical computational methods for processing large numbers. In general scientific calculations, hundreds or more decimal places are often counted, of course, hundreds of billions of large numbers. Generally, such numbers are collectively referred to as high-precision numbers. High-precision algorithms are analog additions, subtractions, multiplies, divides, multipliers, factorials, radicals and other operations of computers for very large data.

In general, we use a continuous space, such as a linear table, a sequential table, an array, and so on, to split each bit of the large number. For example, 4578 can be split into array[0] = 8,array[1] = 7,array[2] = 5,array[3] = 4 to store in an array array array, and it is not fixed whether the higher or lower bit is placed on the array[0] depends on the coder and the environment requirements.

High Precision Addition

A+B=C(A and B are both high precision)
The premise of analogue addition is that we know how to calculate it.

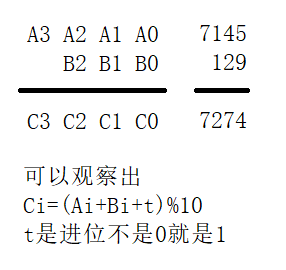
So 7145+129 is
C0=(5+9+0)%10=4
t=(5+9+0)/10=1
C1=(4+2+1)%10=7
t=(4+2+1)/10=0
C2=(1+1+0)%10=2
t=(1+1+0)/10=0
C3=(7+0+0)%10=7
t=(7+0+0)/10=0
Code simulates the above steps
Sample Code (C++)

Insert Generation Here vector<int> add(vector<int>& a, vector<int>& b)
{
    vector<int> c;
    int temp = 0;	//Storage carry
    //a,b must be counted as long as there are characters in it, and a loop is needed when the rounds are valid or the rounds will be discarded resulting in a missing top position
    for (int i = 0; i < a.size() || i < b.size() || temp; i++)
    {
        if (i < a.size())
            temp += a[i];
        if (i < b.size())
            temp += b[i];
        //Must be balanced, e.g. 9+8 = 17, bits 17%10 = 7
        c.push_back(temp % 10);
        //Consider rounding 17/10 = 1
        temp /= 10;
    }
    //Example 9+8 above ends the loop directly if temp is not zero and all loops have to be added if temp is not zero

    return c;
}Chips

High Precision Subtraction

A-B=C(A and B are both high precision)
Simulating subtraction also requires that we know how additions are calculated.

C0=(5-9-0+10)%10=6
t=1 because (5-9-0) <0
C1=(4-2-1+10)%10=1
t=0 because (4-2-1)>0
C2=(1-1-0+10)%10=0
t=0 because (1-1-0)>0
C3=(7-0-0+10)%10=7
t=0 because (7-0-0)>0
The problem here is, what if A<B? Negative numbers are generated. As we all know, negative numbers are generated when A is not enough to subtract B's debts, that is, when B is much less than A, how much A is owed when B is subtracted from B, so when B is greater than A, subtract A from B and add a minus sign.
Code simulates the above rules
Sample Code (C++)

#include <iostream>
#include <vector>
#include <utility>

using namespace std;

pair<char, vector<int>> sub(vector<int>& A, vector<int>& B)
{
    //Store negative signs and numbers
    pair<char, vector<int>> t;
    bool flag = false;  //Is the tag a negative number
    if (A.size() < B.size() || A.back() < B.back())
    {
        //Negative Sign
        flag = true;
        //Exchange minus and subtracted
        A.swap(B);
    }
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i++)
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);//If t<0, debit plus 10, the remaining 10 will not affect, if >=0, 10 plus 10 or T
        if (t < 0) t = 1; //Debit is required when less than 0 
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0)
    C.pop_back();
    //Remove extra 0, such as 100-97=3, to prevent output 03 
    //Is there a negative sign
    if (flag)
        t.first = '-';
    else
        t.first = '+';
    t.second = C;
    return t;
}


int main()
{
    vector<int> a, b, t;
    pair<char, vector<int>> c;
    //Initialization
    //a is 7145 and b is 129
    a.push_back(5);
    a.push_back(4);
    a.push_back(1);
    a.push_back(7);
    b.push_back(9);
    b.push_back(2);
    b.push_back(1);
    //b.push_back(8); // Unscramble this sentence to test negative arithmetic

    c = sub(a, b);
    t = c.second;
    //Output in reverse order because the high digits are at the low position of the container
    //Print out if there is a negative sign
    if (c.first == '-')
        cout << c.first;
    for (auto it = t.rbegin(); it != t.rend(); it++)
        cout << *it;
    return 0;
}

High Precision Multiplication

A*b=C,A is high precision, B is low precision (bits small, you can use int)
Of course, the premise of simulating multiplication is to know how it works

C0=(5x5+0)%10=5
t=(5x5+0)/10=2
C1=(2x5+2)%10=2
t=(2x5+2)/10=1
C2=(1x5+1)%10=1
t=(1x5+1)/10=0

#include <iostream>
#include <vector>

using namespace std;

//C=A*b
vector<int> mul(vector<int>& A, int b)
{
    vector<int> C;
    int t = 0;//Carry-in 0 at initialization
    //Note that if the A digit number is valid, the loop also needs to be valid for the decimal t, otherwise errors will occur and the highest digit will be missing
    for (int i = 0; i < A.size() || t; i++)
    {
        if (i < A.size()) t += A[i] * b;//Multiply b by A[i], each of A[i] by b
        C.push_back(t % 10);  //Multiply and take only the last digit 
        t /= 10;//Consider rounding
    }
    return C;
}

int main()
{
    vector<int> a, c;
    int b;
    //Initialization
    //a is 125, b is 5
    a.push_back(5);
    a.push_back(2);
    a.push_back(1);
    b = 5;

    c = mul(a, b);
    //Output in reverse order because the high digits are at the low position of the container
    for (auto it = c.rbegin(); it != c.rend(); it++)
        cout << *it;
    return 0;
}

High Precision Division

A/b=C,A is high precision, B is low precision (small bits, can use int)

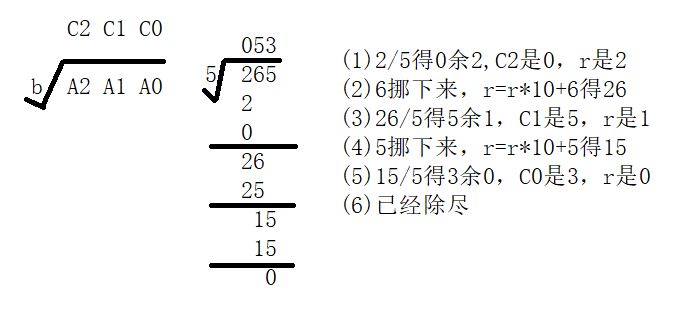
We subtract the remainder from the analysis, such as 26-25 = 1 remaining 1 in the figure, but I can use the remainder (%) directly in the code.
Implement the above simulation in code
Sample Code (C++)

#include <iostream>
#include <vector>

using namespace std;

//A/b, quotient is C, remainder is r 
vector<int> div(vector<int>& A, int b)
{
    vector<int> C;
    int r = 0;
    for (int i = A.size() - 1; i >= 0; i--)
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        //Remainder
        r %= b;
    }
    //Because division starts at a high position, whether there is a leading zero depends on whether there is a leading zero
    while (C.size() > 1 && C.front() == 0)
        C.erase(C.begin()); //Erase the top one
    //Remove extra zeros, such as 15/3 and get 5 instead of 05 
    return C;
}

int main()
{
    vector<int> a, c;
    int b;
    //Initialization
    //a is 125, b is 5
    a.push_back(5);
    a.push_back(2);
    a.push_back(1);
    b = 5;

    c = div(a, b);
    //Since the high position of the division is also at the high position of the container, there is no need to output in reverse order this time. 
    for (auto it = c.begin(); it != c.end(); it++)
        cout << *it;
    return 0;
}

practical application

Title: [Introduction 3] Sum of factorial for cyclic structure P1009 [NOIP1998 universal group]
Resolution: [Introduction 3] Sum of factorials of cyclic structure P1009 [NOIP1998 Popularization Group]