Brushing date: 7:49 am Sunday, May 30, 2021
Personal question brushing records and code collection are all from leetcode
After much discussion and consultation, we now intend to work in the direction of Java
The main answer language is Java
Title:
Sword finger Offer 68 - I. nearest common ancestor of binary search tree
Simple difficulty 131
Given a binary search tree, find the nearest common ancestor of two specified nodes in the tree.
Baidu Encyclopedia The definition of nearest common ancestor in is: "for two nodes p and q with root tree T, the nearest common ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q and the depth of X is as large as possible (a node can also be its own ancestor)."
For example, given the following binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
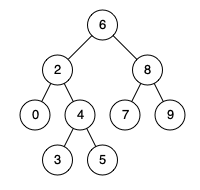
Example 1:
input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 output: 6 explain: The nearest common ancestor of node 2 and node 8 is 6.
Example 2:
input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 output: 2 explain: The nearest common ancestor of node 2 and node 4 is 2, Because according to the definition, the nearest common ancestor node can be the node itself.
explain:
- The values of all nodes are unique.
- p. q is different nodes and exists in a given binary search tree.
Topic analysis
The characteristic of binary search tree is that it is already orderly.
Binary tree problem is likely to involve recursion. In the search, if the left is less than the root and the right is greater than the root, then the root node will be returned directly. If both the left and right are greater than, then go to the right. If both the left and right are less than, then go to the left.
The question defines that the input must exist, so which node to find first and which node is the nearest public node.
Initial answer:
No white practice, no white practice, perfect ending, one-time pass
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
TreeNode res;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val > q.val) {
TreeNode tmp = p;
p = q;
q = tmp;
} //Make sure p is small and q is large
if(root.val <= q.val && root.val >= p.val) return root;
if(root.val < p.val) res = lowestCommonAncestor(root.right, p, q);
if(root.val > p.val) res = lowestCommonAncestor(root.left, p, q);
return res;
}
}
Execution result: passed
Show details add notes
Execution time: 6 ms, beating 100.00% of users in all Java submissions
Memory consumption: 38.6 MB, beating 96.88% of users in all Java submissions
Learn from others:
Method 1:
Gem L2 (edited) February 14, 2020
Java problem solving is simple and clear
Make good use of the properties of binary search tree.
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return null;
if (root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
return root;
}
Method 2:
JoCai 2021-02-21
Java:
Execution time: 6 ms, beating 100.00% of users in all Java submissions
Memory consumption: 39.3 MB, beating 17.36% of users in all Java submissions
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
if(p==root || q==root) return root;
//Both nodes are on the left of the current node
if(p.val<root.val && q.val<root.val){
return lowestCommonAncestor(root.left,p,q);//Find the left
}
//Both nodes are on the right of the current node
else if(p.val>root.val && q.val>root.val){
return lowestCommonAncestor(root.right,p,q);//Look to the right
}
//Or one left and one right
else{
return root;
}
}
}
Method 3:
2020-03-13
You can write a few case s and draw a picture to see. It's easy to find the law
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//When p and q are smaller than root, according to the nature of binary search tree, the common ancestor of p and q must be on the left subtree of root
if (p.val < root.val && q.val < root.val) {
return lowestCommonAncestor(root.left, p, q);
}
//Similarly, when P and Q are larger than root, go to the right subtree of root.
if (p.val > root.val && q.val > root.val) {
return lowestCommonAncestor(root.right, p, q);
}
//If p or q is equal to root, it means that the node equal to is the common ancestor
//Otherwise, p and q are on both sides of root, and root is the common ancestor
if (p.val == root.val) {
return p;
} else if (q.val == root.val) {
return q;
} else {
return root;
}
}
}
Method 4:
Roderland 2020-08-06
Iterative version
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// if (p==root||q==root) return root;
// if (p==q) return p;
while (true) {
if (root.val>p.val&&root.val>q.val) root=root.left;
else if (root.val<p.val&&root.val<q.val) root=root.right;
else return root;
}
}
}
Method 5
K God
Author: jyd
Link: https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-i-er-cha-sou-suo-shu-de-zui-jin-g-7/
Source: LeetCode
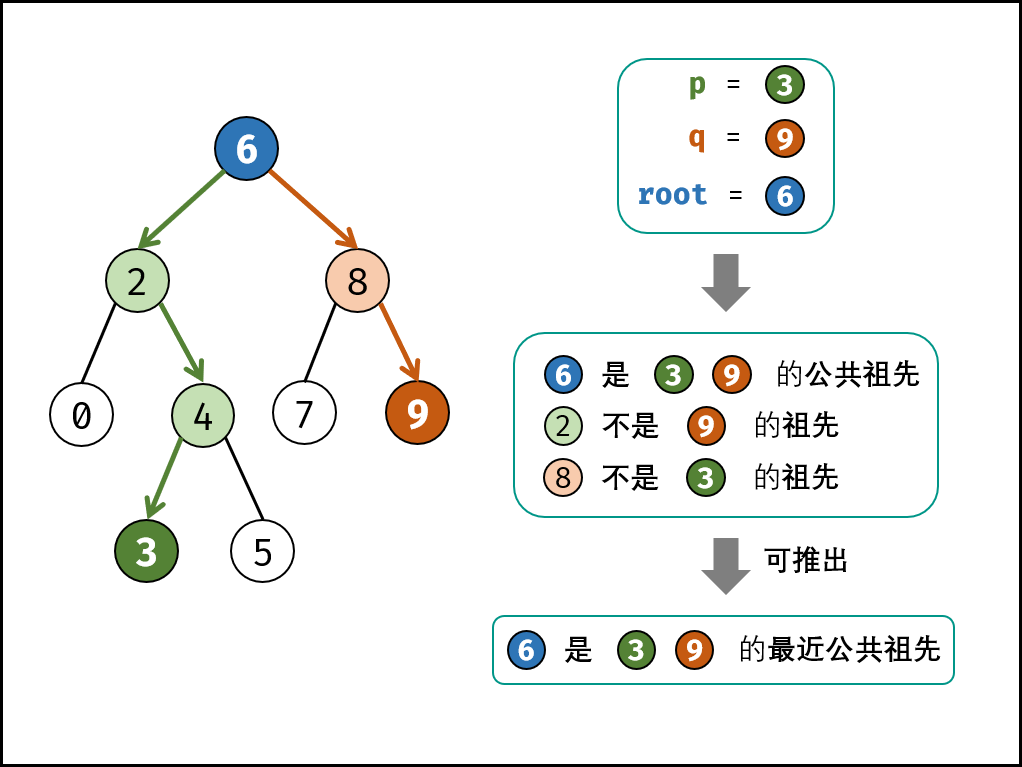
Method 1: iteration
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root != null) {
if(root.val < p.val && root.val < q.val) // p. Q is in the right subtree of root
root = root.right; // Traverse to the right child node
else if(root.val > p.val && root.val > q.val) // p. Q is in the left subtree of root
root = root.left; // Traverse to the left child node
else break;
}
return root;
}
}
Optimization: if p.val < q.val can be guaranteed, the judgment conditions can be reduced in the cycle.
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val > q.val) { // Guarantee p.val < q.val
TreeNode tmp = p;
p = q;
q = tmp;
}
while(root != null) {
if(root.val < p.val) // p. Q is in the right subtree of root
root = root.right; // Traverse to the right child node
else if(root.val > q.val) // p. Q is in the left subtree of root
root = root.left; // Traverse to the left child node
else break;
}
return root;
}
}
Method 2: recursion
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
if(root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
return root;
}
}
Title:
Sword finger Offer 68 - II Nearest common ancestor of binary tree
Simple difficulty 258
Given a binary tree, find the nearest common ancestor of two specified nodes in the tree.
Baidu Encyclopedia The definition of nearest common ancestor in is: "for two nodes p and q with root tree T, the nearest common ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q and the depth of X is as large as possible (a node can also be its own ancestor)."
For example, give the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
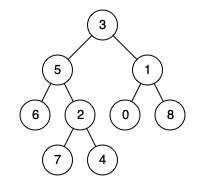
Example 1:
input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 output: 3 explain: The nearest common ancestor of node 5 and node 1 is node 3.
Example 2:
input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 output: 5 explain: The nearest common ancestor of node 5 and node 4 is node 5. Because according to the definition, the nearest common ancestor node can be the node itself.
explain:
- The values of all nodes are unique.
- p. q is different nodes and exists in a given binary tree.
Topic analysis
Instead of searching a binary tree, you must find two nodes before it ends.
Goo Goo L1 (edited) 2021-05-04
The recursive understanding of this problem is actually not so simple. If the function is directly understood as finding the nearest ancestor node of pq in the tree with root as the root, it is not accurate. The definition of this recursive function should be extended. In fact, the functions of this function are:
- If there are pq two nodes in the tree with root, the nearest ancestor is returned
- If there is only one node in the tree with root as the root, the node containing is returned
- If neither node exists, nullptr is returned
After expanding the definition of the function, it conforms to the logic of the return value in the function body, and can just realize the required functions.
Initial answer:
Refer to the above analysis and solutions
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null) return right;
if(right == null) return left;
return root;
}
}
Execution result: passed
Show details add notes
Execution time: 7 ms, beating 99.98% of users in all Java submissions
Memory consumption: 39.9 MB, beating 45.15% of users in all Java submissions
Learn from others:
Method 1:
...L1 (edited) February 13, 2020
class Solution {
/**
* Nearest common ancestor of binary tree
* Idea:
* Three situations:
* 1,p q If one is in the left subtree and the other is in the right subtree, the current node is the nearest common ancestor
* 2,p q All in the left subtree
* 3,p q All in the right subtree
* @param root
* @param p
* @param q
* @return
*/
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return null;
}
if (root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
// p q one on the left and one on the right
return root;
}
if (left != null) {
// Both P and Q are in the left subtree
return left;
}
if (right != null) {
// Both P and Q are in the right subtree
return right;
}
return null;
}
}
Method 2:
(edited) March 17, 2021
The practice in the book of sword finger offer is not time efficient, but it is also easy to understand
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Deque<TreeNode> stackP = new ArrayDeque<>();
Deque<TreeNode> stackQ = new ArrayDeque<>();
getTrace(root,p,stackP); // Get the path of p and q
getTrace(root,q,stackQ);
TreeNode ret = root;
while(!stackP.isEmpty()&&!stackQ.isEmpty()){
TreeNode nodeQ = stackQ.poll();
TreeNode nodeP = stackP.poll();
if(nodeP.val!=nodeQ.val) return ret;
ret = nodeP; //ret is the last same node
}
return ret;
}
private boolean getTrace(TreeNode root , TreeNode node, Deque<TreeNode> stack){
stack.addLast(root);
boolean hasGet=false;
if(root.val == node.val) return true;
if(root.left!=null) hasGet = getTrace(root.left,node,stack);
if(!hasGet && root.right!=null&&!stack.isEmpty()) hasGet = getTrace(root.right,node,stack);
if(!hasGet&&!stack.isEmpty()) stack.removeLast();
return hasGet;
}
}
The follow-up traversal is time-efficient and the code is concise and beautiful, but it doesn't feel very good_ ( ¦ 3」∠)_
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null||root==p||root==q) return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left!=null && right!=null) return root;
if(left!=null) return left;
if(right!=null) return right;
return null;
}
}
Method 3:
Brise Three days ago
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){return null;}
if(root==p||root==q){return root;}
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left ==null){
return right;
}else if(right==null){
return left;
}else{
return root;
}
}
}
Method 4:
Bad morisheng L1 2020-10-28
p and q are the nodes in the tree;
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null)
return null;
if(p == root || q == root)
return root;
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left != null && right != null)
return root;
return left == null ? right : left;
}
}
Method 5
K God
Author: jyd
Link: https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-ii-er-cha-shu-de-zui-jin-gong-gon-7/
Source: LeetCode
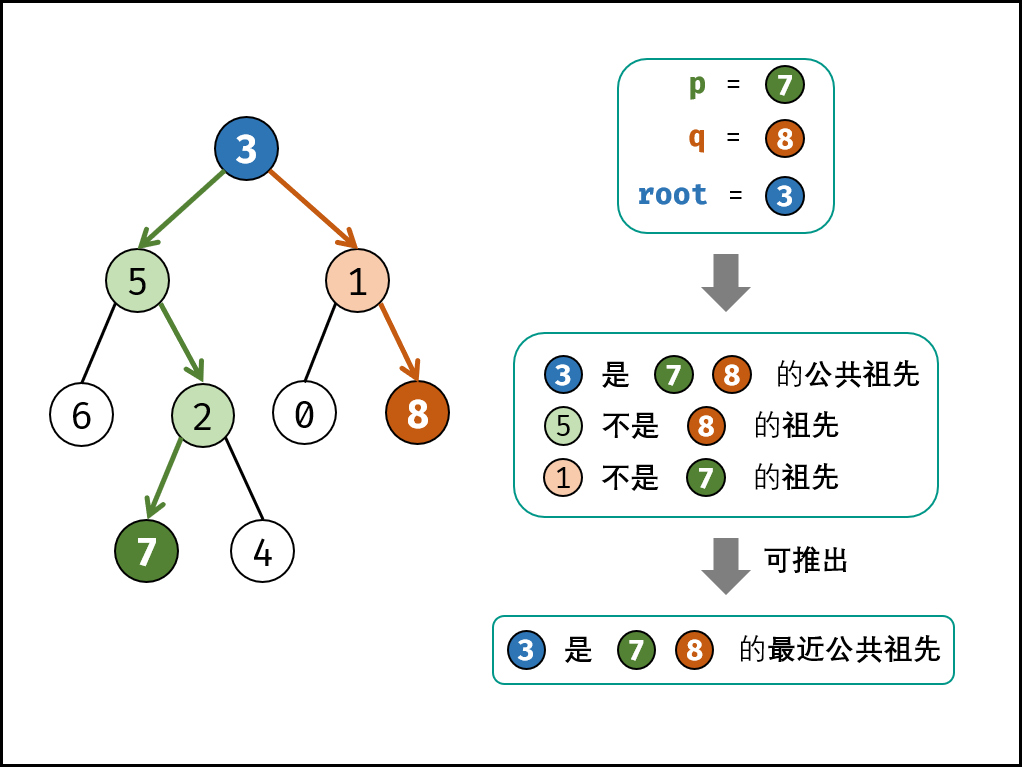
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null) return right;
if(right == null) return left;
return root;
}
}
Expanded writing
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right == null) return null; // 1.
if(left == null) return right; // 3.
if(right == null) return left; // 4.
return root; // 2. if(left != null and right != null)
}
}
summary
The above is the content and learning process of this topic. Basically, there is a cycle when there is recursion. There have been two months intermittently. Then there is review, and then brush the topic to maintain the feel. Come on, everyone.
Sprinkle flowers at the end~
Welcome discussion and common progress.