Depth first search pruning

We have learned that the search process will eventually generate a search tree.
Pruning, as the name suggests, is to cut down unnecessary subtrees on the search tree through some judgment. Sometimes, we will find that the state of the subtree corresponding to a node is not the result we want, so we don't need to search this branch. Cutting off this subtree is pruning.

Feasible pruning

The problem discussed before: given n integers, K numbers are required to be selected so that the sum of the selected K numbers is sum

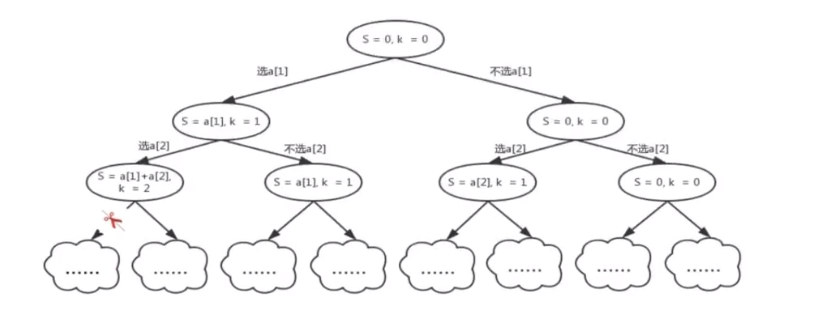
As shown in the figure above, when k= 2, if two numbers have been selected, it is meaningless to select more numbers later. So we can directly subtract this search branch from the subtree subtracted by the scissors in the figure above.
For another example, if all numbers are positive, if the current sum value is found to be greater than sum, then no matter how the sum value is selected, it is impossible to return to sum. We can also directly terminate the search of this branch.
In the search process, once we find that some states cannot find the final solution anyway, we can "prune" them.

Type example: select k numbers from n numbers so that sum is m

dfs

Select 8 numbers from the 30 numbers 0, 1, 2,..., 29, so that the sum value is 200.

# The sum of 1 choices is 200
# From 0,1,2, 29 select 8 of the 30 numbers so that the sum value is 200.

# i from the first place, cnt currently selects several numbers, and s selects the sum of the numbers
def dfs(i,cnt,s):
	if i == n :
		if cnt == k and s == sumnum:
			# To modify a global variable, declare it first
			global ans
			ans = ans + 1
		return 1
	# There are two possibilities: 1 Don't choose to enter the next 2 Select this number to go to the next one
	dfs(i+1,cnt,s)
	dfs(i+1,cnt+1,s+a[i])

n = 30
k = 8
sumnum = 200
# Data storage array
a = []
for i in range(0,30):
	a.append(i)
print(a)

ans = 0
dfs(0,0,0)
print(ans)

The running time is very long. Prune it to shorten the computing time of the computer

Depth first search (dfs) pruning

# The sum of 1 choices is 200
def dfs(i,cnt,s):
    # --------Pruning part
	if cnt > k:
		return 1
	if s > sumnum:
		return 1
    # --------Pruning part
	if i == n :
		if cnt == k and s == sumnum:
			# To modify a global variable, declare it first
			global ans
			ans = ans + 1
		return 1
	# There are two possibilities: 1 Don't choose to enter the next 2 Select this number to go to the next one
	dfs(i+1,cnt,s)
	dfs(i+1,cnt+1,s+a[i])

test result

Data at 0-29 Choose between 8 numbers: 5
 Data in 1-30 Choose between 8 numbers: 70

Optimal pruning

For a class of problems seeking the optimal solution, the optimality pruning can usually be used. For example, when solving the shortest path of the maze, if it is found that the current number of steps has exceeded the current optimal solution, the search from the current state is redundant, because the search will never find a better solution. Through such pruning, a large number of redundant calculations can be saved.
In addition, in the process of searching whether there is a feasible solution, once a set of feasible solutions are found, all the subsequent searches do not have to be carried out, which is a special case of optimality pruning.

There is a maze the size of n x m. The character'S' represents the starting point, the character'T 'represents the ending point, the character' * 'represents the wall and the character' Indicates flat ground. You need to start from'S' to'T ', you can only move up, down, left and right adjacent positions at a time, and you can'T get out of the map or enter the wall. There are at least one possible path from T 'to S'.

Usually we use BFS (breadth first search) to solve this problem, and the first result we find is the answer.

Now let's consider using DFS (depth first search) to solve this problem. The answer ans found in the first search is not necessarily a positive solution, but the positive solution must be less than or equal to ans. therefore, if the current number of steps is greater than or equal to ans, prune directly, and update ans every time a feasible answer is found

Type example: maze problem (minimum steps)

# 2 maze problem pruning
# Define the global variables used
# ranks
n , m = [int(i) for i in input("").split()]

# Map form for storing mazes
maze = []
for i in range(0,n):
	list1 = list(input(""))
	maze.append(list1)
# Whether the location where the map is stored has been passed and marked
vis = []
for i in range(0,n):
	list1 = [0]*m
	vis.append(list1)
# Default steps
ans = 1000

def dfs(x,y,step):
	global ans 
	# ----------Pruning part
	if step >= ans:
		return 1
	# -----------Pruning part
	if maze[x][y] == 'T':
		if step < ans:
			ans = step
		return 1
	# Mark
	vis[x][y] = 1
	maze[x][y] = 'm'
	# Store the direction into the array (counterclockwise)
	direction = [[-1,0],[0,-1],[1,0],[0,1]]
	for i in range(0,len(direction)):
		tx = x + direction[i][0]
		ty = y + direction[i][1]
		if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0:
			dfs(tx,ty,step+1)

	#If not found, cancel the relevant mark
	vis[x][y] = 0
	maze[x][y] = '.'
	return 0

# Find starting position
for i in range(0,n):
	for j in range(0,m):
		if maze[i][j] == "S":
			x = i
			y = j

dfs(x,y,0)
print(ans)

Repetitive pruning

For some specific search methods, a scheme may be searched many times, which is unnecessary.
Let's look at this question:
Given n integers, it is required to select k numbers so that the sum of the selected K numbers is sum.
If the search method is to select one number from the remaining numbers at a time and search the k-th layer in total, then the selection method of 1, 2 and 3 can be searched for 6 times, which is unnecessary, because we only focus on the sum of the selected numbers and will not focus on the order of the selected numbers at all, so we can use repetitive pruning here.

#The sum of 3 choices is 200 pruning
# From 0,1,2, 29 select 8 of the 30 numbers so that the sum value is 200.

# s is the sum, cnt is the count of the selected number, and pos is the position of the last selected number
def dfs(s,cnt,pos):
	if s > sumnum or cnt > k:
		return 1 

    if s == sumnum and cnt == k:
    	global ans
        ans = ans + 1

    for i in range(pos,n):
        if xuan[i] == 0:  
            xuan[i] = 1
            dfs(s + a[i], cnt + 1 , i+1)
            xuan[i] = 0

n = 30
k = 8
sumnum = 200
# Data storage array
a = []
xuan = []
for i in range(0,30):
	a.append(i+1)
	xuan.append(0)
print(a)

ans = 0
dfs(0,0,0)
print(ans)
#There is a problem with the test code

Parity pruning

I didn't learn very well

Practice of detonating a bomb

Detonate the bomb

On an n x m grid map, bombs are placed on some grids. After manually detonating a bomb, the bomb will detonate all the bombs on the row and column where the bomb is located, and the detonated bomb can detonate other bombs. In this way, the chain will continue.

Now, in order to detonate all the bombs on the map, you need to detonate some of them manually. In order to minimize the risk, please calculate how many bombs can detonate all the bombs on the map manually.

In the map, 1 means there is a bomb and 0 means there is no bomb

explain

We put the bombs that can detonate each other into a set, and the final number of sets is the answer we ask. Obviously, the effect of detonating any bomb in a set is the same. We can traverse all bombs in the grid of n x m. if the current bomb has not been detonated before, detonate it, that is, mark all bombs in its set.
DFS can be used to search the set where a bomb is located. After each bomb is detonated, it will search whether there are other bombs in its ranks, and then continue the search. Because there are nx m bombs at most, after each bomb is detonated, check whether there are bombs in the N + m grids in the row and column. The time complexity is O(nm(n + m)).
Here is a pruning. Each row and column only need to be searched once at most, so you can mark the searched rows and columns to avoid repeated search. In this way, each grid can be checked twice at most, and the time complexity becomes O(nm).

code

# 4 detonate the bomb

def boom(x,y):
	# The place where 1 is a bomb has been visited
	# If it is not marked, it will cause repeated detonation of this position during subsequent row and column search
	maze[x][y] = 0
	# Line marking
	if row[x] == 0:
		# Indicates that the line was detonated
		row[x] = 1
		# Find the bomb in the line in the map and detonate it
		for i in range(0,m):
			if maze[x][i] == 1:
				boom(x,i)
	# Tag column
	if col[y] == 0:
		# Indicates that the column was detonated
		col[y] = 1
		# Find the bomb in this column in the map and detonate it
		for j in range(0,n):
			if maze[j][y] == 1:
				boom(j,y)
	

# ranks
n , m = [int(i) for i in input("").split()]
# Bomb map
maze = []
# Row array
row = []
# Column array
col = []

for i in range(0,n):
	list1 = [int(j) for j in list(input(""))]
	maze.append(list1)

for i in range(0,n):
	row.append(0)

for i in range(0,m):
	col.append(0)

cnt = 0
for i in range(0,n):
	for j in range(0,m):
		if maze[i][j] == 1:
			cnt = cnt + 1
			boom(i,j)
print(cnt)
print(maze)
print(row)
print(col)

Birthday cake exercise

Birthday cake topic

Today is sister Hua's birthday. Garlic Jun plans to make an m-layer birthday cake with a volume of n π for her. Each layer of cake is a cylinder. Let the i(0 ≤ I < m) layer of cake from bottom to top be a cylinder with radius Ri and height Hi. When I > 0, it is required R i R_i Ri​< R i − 1 R_{i-1} Ri − 1 − and H i H_i Hi​< H i − 1 H_{i-1} Hi−1​.
Since we need to spread cream on the cake, in order to save money as much as possible, we want the area Q of the outer surface of the cake (except the bottom surface of the lowest layer) to be the smallest. Let Q = S π, please program the given n and m to find out the cake making scheme (appropriate) R i R_i Ri and H i H_i Hi) to minimize S. (except Q, all the above data are positive integers)

explain

For the convenience of narration, the surface area and volume of this question are the result of dividing by π, and the surface area refers to the surface area after removing the lower bottom surface.
The volume of the whole cake n π = ∑ i = 0 m − 1 R i 2 ∗ π ∗ H i nπ=\sum_{i=0}^{m-1} R^2_i*π*H_i nπ=∑i=0m−1​Ri2​∗π∗Hi​

Surface area Q = R 0 2 ∗ π + 2 π ∑ i = 0 m − 1 R i ∗ H i Q=R_0^2*π+2π\sum_{i=0}^{m-1}R_i*H_i Q=R02​∗π+2π∑i=0m−1​Ri​∗Hi​
Because the radius and height of each cylinder are positive integers, the maximum value cannot be obtained directly by mathematical method, and the answer can only be found by DFS search.
It is easy to find that except for layer 0, when the volume is certain, R i R_i The larger Ri, the larger the surface area. In this way, we will enumerate from large to small in the search process R i R_i Ri is more conducive to subsequent pruning optimization.

Now when we think about layer i, R i R_i Ri and H i H_i Enumeration range of Hi.
Title Requirements R i R_i Ri​ < R i − 1 R_{i-1} Ri − 1, while R i R_i Ri ， must be a positive integer, then because R m − 1 R_{m-1} Rm − 1 ≥ 1, it can be pushed out R i R_i Ri​≥m- i.
Therefore, when I > 0, R i R_i Ri​∈[m-i, R i − 1 R_{i-1} Ri−1​-1]. Similarly, H ∈ [m-i, H i − 1 H_{i-1} Hi−1​ - 1].
Bottom layer R 0 < = n R_0<=\sqrt{n} R0​<=n ​, H 0 < = n H_0<=n H0​<=n.
In this way, we prune the scope of each layer of enumeration.

Sometimes, the volume of the current situation is too large, so that even if the volume of the following layers is minimized, the final volume cannot be equal to n.
Let's open an array, va preprocess, and count the minimum volume sum of the first i cylinders from top to bottom. Obviously, va [] is equal to ∑ j = 1 i j 3 \sum_{j=1}^ij^3 ∑j=1i​j3. Then we can use this va array for feasibility pruning in the search.

Next, we consider optimal pruning. If you have found an answer ans, and the current surface area is s and the current volume is v, if S + x > = ans, you can prune.
Where x is the minimum surface area from layer i to layer m - 1. We can't calculate this x before searching, but we can estimate a value y according to the current situation, which satisfies y ≤ X. We prune when s + y ≥ ans. obviously, the closer y is to x, the better the pruning effect is.
Let's find this y by scaling the inequality:
When you are currently on layer i, because
x = 2 ∑ j = i m − 1 R j ∗ H i = 2 / R i ∗ ∑ j = i m − 1 R i ∗ R j ∗ H i > = 2 / R i ∗ ∑ j = i m − 1 R j 2 ∗ H j = 2 ( n − v ) / R i = y x=2\sum_{j=i}^{m-1}R_j*H_i=2/R_i*\sum_{j=i}^{m-1}R_i*R_j*H_i>=2/R_i*\sum_{j=i}^{m-1}R_j^2*H_j=2(n-v)/R_i=y x=2j=i∑m−1​Rj​∗Hi​=2/Ri​∗j=i∑m−1​Ri​∗Rj​∗Hi​>=2/Ri​∗j=i∑m−1​Rj2​∗Hj​=2(n−v)/Ri​=y

So we just need to s + 2 ( n − v ) / R i > = a n s s+2(n-v)/R_i>=ans s+2(n − v)/Ri > = ans for optimal pruning.

X > = ans, you can prune.
Where x is the minimum surface area from layer i to layer m - 1. We can't calculate this x before searching, but we can estimate a value y according to the current situation, which satisfies y ≤ X. We prune when s + y ≥ ans. obviously, the closer y is to x, the better the pruning effect is.
Let's find this y by scaling the inequality:
When you are currently on layer i, because
x = 2 ∑ j = i m − 1 R j ∗ H i = 2 / R i ∗ ∑ j = i m − 1 R i ∗ R j ∗ H i > = 2 / R i ∗ ∑ j = i m − 1 R j 2 ∗ H j = 2 ( n − v ) / R i = y x=2\sum_{j=i}^{m-1}R_j*H_i=2/R_i*\sum_{j=i}^{m-1}R_i*R_j*H_i>=2/R_i*\sum_{j=i}^{m-1}R_j^2*H_j=2(n-v)/R_i=y x=2j=i∑m−1​Rj​∗Hi​=2/Ri​∗j=i∑m−1​Ri​∗Rj​∗Hi​>=2/Ri​∗j=i∑m−1​Rj2​∗Hj​=2(n−v)/Ri​=y

So we just need to s + 2 ( n − v ) / R i > = a n s s+2(n-v)/R_i>=ans s+2(n − v)/Ri > = ans for optimal pruning.

Rookies find it too difficult to write the code.