1. Illustrating data structures
1. Infrastructure
(1) Arrays
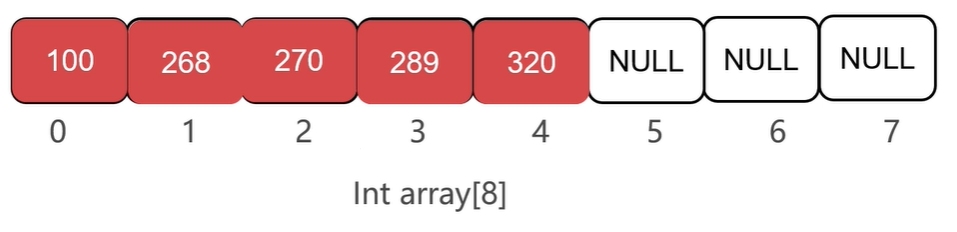
Arrays are essentially a continuous block of memory that holds something in common. Array elements can be quickly positioned and manipulated through array subscripts. However, its insertion and deletion operations are inconvenient, requiring all elements following the insertion or deletion positions to be moved.
- Advantages: Continuous memory, fast addressing with subscripts;
- Disadvantages: it is difficult to insert and delete nodes;
(2) Single-chain list
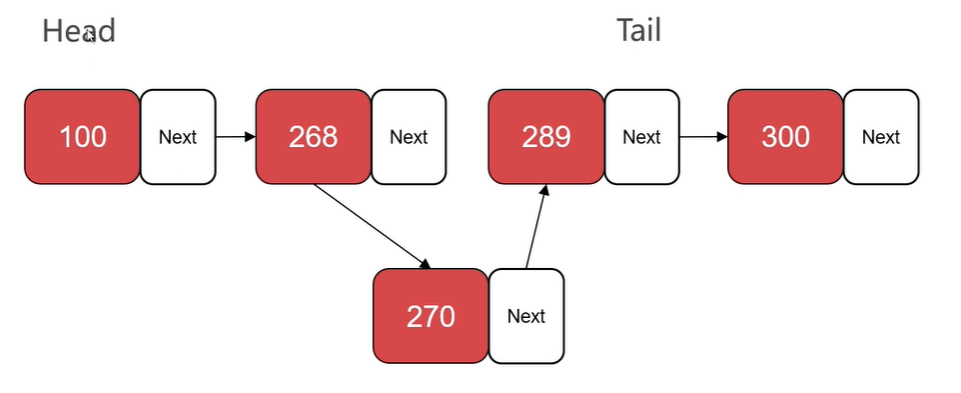
A node of a single-linked list usually consists of a data data field and a next pointer field. At the same time, head and tail pointers are usually used to point to the head and tail of the chain table, respectively.
When inserting or deleting a node in a chain table, you only need to find the corresponding location for pointer operation, and you do not need to move other elements. However, querying elements in a chain table requires traversing the entire chain table, which is more difficult, i.e. the query complexity is O(n)
- Advantages: Easy to insert and delete data;
- Disadvantages: inefficient query;
2. HashMap
HashMap is also essentially a container for storing data. For fast indexing purposes, HashMap uses the fast positioning feature of arrays, which establishes the relationship between the insertion value and the array subscript.
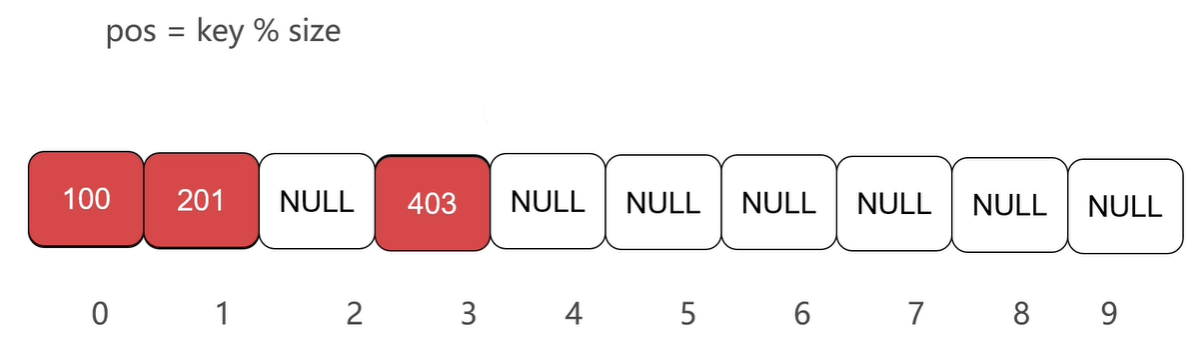
Assume an array of type int, and the relationship is p o s = k e y % s i z e pos = key \% size pos=key%size. The key here is to insert the contents of the data, the size is the length of the array, and the pos is the array subscript. If the inserted element is 100 and its calculated position is 0, it is inserted at 0. When querying elements, it is also based on such a relationship that the location of elements is first calculated, then blanked out, and if there are elements, then compared for equality.
There is a problem with the above process, such as inserting another element with a value of 200 at this time, which can cause problems with array insertion and data conflicts. You can now introduce the property of a chain table, which declares each element of an array as a chain node.
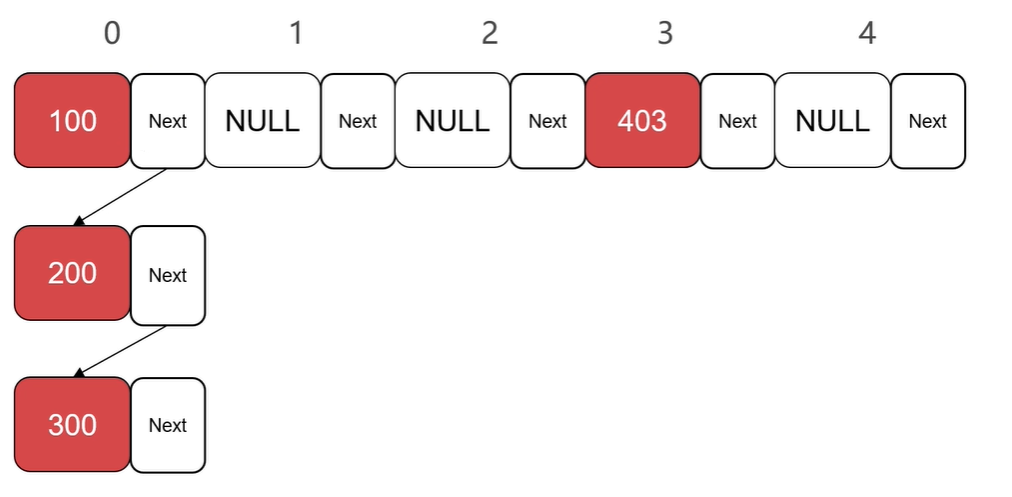
When a conflict occurs between the corresponding subscripts resulting from the established relationship, a single-chain table can be used to expand it. In this case, when looking for an element, it first locates at the corresponding index location, and then searches for the corresponding element in turn on the chain table extended by that location. For example, when looking for an element of 200, find the 0 position first, then compare the corresponding node elements in the expanded list order, and find the corresponding element when comparing to 200.
It is not difficult to find that there is still a problem at this time. If the extended single-chain table is very long, the query time is very long, so the query efficiency of the chain table is low and the time complexity is O(n). In this way, the need to quickly locate element targets cannot be achieved. Therefore, HashMap is in Java1. After 8, some optimizations were made, and the red-black tree structure was introduced.
Red-black tree is a special kind of binary tree. It is a highly balanced tree. The query efficiency of a binary tree is the depth of the tree, which is obviously more efficient than a single-chain list query. The balanced binary tree guarantees its own height balance and high insertion performance, while the red and black trees absorb the characteristics of the balanced binary tree and make some adjustments to the insertion.
The use of red-black trees in HashMap is to convert single-chain lists into red-black trees to improve query performance when the extended single-chain lists are too long.
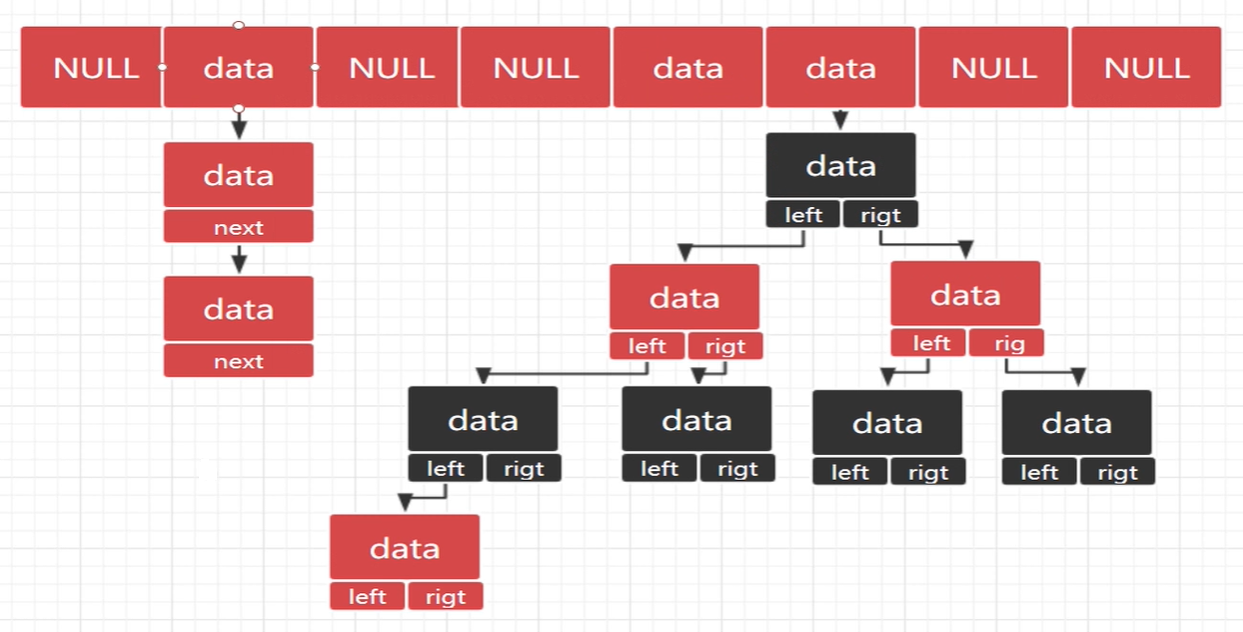
Summary:
- The data structures used by HashMap include initial arrays, chain lists, and red and black trees.
- Use when inserting data k e y % s i z e key \% size key%size to insert data;
- When two or more keys have the same pos value and different key values (in conflict), they hang after the chain table in the initialization position of the array.
- When there are too many chain table nodes behind a certain node, it is converted to a red-black tree to improve efficiency.
2. Source Code Analysis
1. Creation of HashMap
HashMap is constructed as follows:
/**
* Constructs an empty <tt>HashMap</tt> with the default initial capacity
* (16) and the default load factor (0.75).
*/
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
The loadFactor in the above code is the load factor for HashMap, where the default load factor is DEFAULT_LOAD_FACTOR 0.75
/** * The load factor used when none specified in constructor. */ static final float DEFAULT_LOAD_FACTOR = 0.75f;
2. HashMap node insertion
2.1 The underlying data structure of HashMap
The underlying data structure of HashMap is a Node array, as follows:
/** * The table, initialized on first use, and resized as * necessary. When allocated, length is always a power of two. * (We also tolerate length zero in some operations to allow * bootstrapping mechanics that are currently not needed.) */ transient Node<K,V>[] table;
Node is an internal class of nodes and contains the following data:
/**
* Basic hash bin node, used for most entries. (See below for
* TreeNode subclass, and in LinkedHashMap for its Entry subclass.)
*/
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
... // Method Omitting
}
You can see that it is a single-chain list node structure.
2.2 resize function (including expansion process) (focus!!!)
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table; // Assign the original table to oldTable
int oldCap = (oldTab == null) ? 0 : oldTab.length; // Get the space size of the original table
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) { // static final int MAXIMUM_CAPACITY = 1 << 30;
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY) // Doubling capacity
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY; // static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); // 12
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr; // Assign to threshold
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; // Request real memory space
table = newTab; // Assign to members within a class
if (oldTab != null) { // Insert nodes from the original table into the new table
for (int j = 0; j < oldCap; ++j) { // Loop every position in the original table
Node<K,V> e;
if ((e = oldTab[j]) != null) { // Determine if the location is null
oldTab[j] = null;
if (e.next == null) // If e.next is null, there is no conflict chain table formed at that location
newTab[e.hash & (newCap - 1)] = e; // Calculate the new location in the new table
else if (e instanceof TreeNode) // If it is a tree node, it is treated as a tree node
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
Expansion process:
Original capacity (16): 0001 0000
n-1(15): 0000 1111
New capacity (32 bit left): 0010 0000
n-1(31): 0001 1111
(1) Assume a hash value of K 1: 0001 0100
The process of logical calculation from the source code:
The subscript j in the original table is ((n-1) &hash): 0000 0100
So hash and oldCap at this point don't result in zero, so
The new subscript is to add to the original capacity (j+oldCap): 0001 0100
The new subscript in the actual new table is:
(n-1)&hash: 0001 0100
(2) Assume that there is a hash value of K 2: 0000 0100
The process of logical calculation from the source code:
The subscript j in the original table is ((n-1) &hash): 0000 0100
So at this point hash and oldCap do the &operation with a result of 0, so
The new subscript is the same j:0000 0100 as the original subscript
If the index position in the new table is calculated directly, then:
The n-1 (31) of the new capacity is: 0001 1111
At this time the new subscript is: 0000 0100
Summary:
- When e.hash & oldCap == 0, the node's index value in the new array is the same as the old index value.
- When e.hash & oldCap!= 0, then the index value of the node in the new array is the old index value + the old array capacity.
Reason:

Be careful:
- JDK7 uses header interpolation, which places new values at the beginning of a chain table, causing the old and new chains to be inverted after expansion (under multithreaded concurrent operations, a ring chain table may be formed, resulting in an endless loop)
- This BUG was fixed in JDK8 using tail insertion, but data loss may occur in concurrent environments.
2.3 treeifyBin function
Converting a chain table to a function of a red-black tree when the conflict resolution chain table in HashMap is longer than 8
/**
* Replaces all linked nodes in bin at index for given hash unless
* table is too small, in which case resizes instead.
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) // Determine if table s need to be resized
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
2.4 Node Insert Related Function
The node insertion function for HashMap is as follows
/**
* Associates the specified value with the specified key in this map.
* If the map previously contained a mapping for the key, the old
* value is replaced.
*
* @param key key with which the specified value is to be associated
* @param value value to be associated with the specified key
* @return the previous value associated with <tt>key</tt>, or
* <tt>null</tt> if there was no mapping for <tt>key</tt>.
* (A <tt>null</tt> return can also indicate that the map
* previously associated <tt>null</tt> with <tt>key</tt>.)
*/
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
/**
* Implements Map.put and related methods.
*
* @param hash hash for key
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0) // Determine if the current HashMap container is empty
n = (tab = resize()).length; // Allocate new capacity and get new capacity size
if ((p = tab[i = (n - 1) & hash]) == null) // Determine index by (n - 1) & hash
tab[i] = newNode(hash, key, value, null); // Create a new Node if the current index position is empty
else { // Hash conflict occurred
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k)))) // Determine if hash and key values are the same
e = p;
else if (p instanceof TreeNode) // If p is a tree node, insert it as a red-black tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) { // If p.next is null, the end node of the list is found
p.next = newNode(hash, key, value, null); // Interpolate to create a new node at the end of the chain table corresponding to the position of the p-index element
// static final int TREEIFY_THRESHOLD = 8;
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash); // Conversion from Single-Chain Table to Red-Black Tree
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k)))) // //Determine if hash and key values are the same, and if they are the same, find elements that already exist
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null) // Modify existing element values only when the onlyIfAbsent parameter is False
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount; // Modifications plus 1
if (++size > threshold) // Determine if the number of nodes currently increasing is greater than the threshold
resize();
afterNodeInsertion(evict);
return null;
}
For further illustration, the following examples can be used:
(1) n = 16, binary representation 0001 0000
Then the binary representation of n-1 is 0000 1111
If the hash value at this point is 0000 0001, the final result is 0000 0001
If the hash value is 0001 0000, the result is 0000 0000
(2) n=15, binary representation 0000 1111
Then the binary representation of n-1 is 0000 1110
If the hash value is 0000 0001 at this time, the final result is 0000 0000
If the hash value is 0001 0000, the result is 0000 0000
You can see that when n is a power of two, a formula is satisfied: (n - 1) & hash = hash% n.
So why must n be a power of two?
Because when n is a power of two, the binary of n-1 must be in the format..11111111, which calculates the position (&) entirely depending on the resulting hash value and is not affected by n-1, which is the binary of the length of the array.
When n is a different value, n-1 may appear...11011 in a similar format, and a hash conflict may be increased by an &operation
Why 2.5 Capacity is Power 2 (Common Interview Examination)
There are three main reasons:
- Since the operating system usually requests memory with a power of two, declaring it to be a power of two can avoid memory fragmentation.
- You can use more efficient bitwise operations;
- Can participate in hash operations (n - 1) & hash to improve the hash of the results.
2.6 Hash Conflict Reduction Method (Interview Score)
Functions that get hash values for key s in HashMap:
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
If the key is not null, the hashCode method of the key is called to return its hash value, then the XOR operation is performed after 16 bits are unsigned right-shifted.
Examples:
Array size n is: 00000000 00001 00000 00000 00000000 00000
Then n-1 is: 00000000 00000 11111 11111111 11
(1) If the original value 1 is: 10010001 10010101 10110000 11110001
Right shift 16 bits: 00000000 00000 10010001 10010101
XOR: 10010001 10010101 00100001 01100100
If n-1 and the original value 1 are directly & operated on, the result is:
00000000 00000000 10110000 11110001
The original value 1 is unsigned, right-shifted 16 bits, XOR is performed, and then n-1 is operated on. The result is:
00000000 00000000 00100001 01100100
(2) If the original value 2 is: 00010001 10010101 10110000 11110001
Right shift 16 bits: 00000000 00000 00010001 10010101
XOR: 10010001 10010101 10100001 01100100
If n-1 and the original value 2 are directly & operated on, the result is:
00000000 00000000 10110000 11110001
The original 2 unsigned right shift 16 bits, then XOR and n-1 & operation, the result is:
00000000 00000000 10100001 01100100
The comparison results show that the original values 1 and 2 are directly the same as n-1, although their own values are not the same. However, a shift XOR operation followed by an n-1 operation yields different results, which reduces hash conflicts and increases hash.
In summary, the XOR operation of hashCode with itself after 16-bit right shift is designed to mix the high-bit and low-bit feature information of hash values and increase the low-bit randomness. If you do not do the XOR operation of the shift just now, you will lose the high area feature when calculating the slot position
3. Queries for HashMap
The node query function for HashMap is as follows
/**
* Returns the value to which the specified key is mapped,
* or {@code null} if this map contains no mapping for the key.
*
* <p>More formally, if this map contains a mapping from a key
* {@code k} to a value {@code v} such that {@code (key==null ? k==null :
* key.equals(k))}, then this method returns {@code v}; otherwise
* it returns {@code null}. (There can be at most one such mapping.)
*
* <p>A return value of {@code null} does not <i>necessarily</i>
* indicate that the map contains no mapping for the key; it's also
* possible that the map explicitly maps the key to {@code null}.
* The {@link #containsKey containsKey} operation may be used to
* distinguish these two cases.
*
* @see #put(Object, Object)
*/
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
/**
* Implements Map.get and related methods.
*
* @param hash hash for key
* @param key the key
* @return the node, or null if none
*/
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// Determine if the table in HashMap is null, or if the length is 0, or if the index position of the corresponding element is null
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Comparing Hash value with key value, returning directly equal
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// Traverse through a single-chain list or a red-black tree node at the corresponding location to find the corresponding element
if ((e = first.next) != null) {
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
4. HashMap Delete Nodes
The node deletion function for HashMap is as follows
/**
* Removes the mapping for the specified key from this map if present.
*
* @param key key whose mapping is to be removed from the map
* @return the previous value associated with <tt>key</tt>, or
* <tt>null</tt> if there was no mapping for <tt>key</tt>.
* (A <tt>null</tt> return can also indicate that the map
* previously associated <tt>null</tt> with <tt>key</tt>.)
*/
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
/**
* Implements Map.remove and related methods.
*
* @param hash hash for key
* @param key the key
* @param value the value to match if matchValue, else ignored
* @param matchValue if true only remove if value is equal
* @param movable if false do not move other nodes while removing
* @return the node, or null if none
*/
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
// The previous logic is basically the same as the node query logic, except that a node is found and assigned to a node object
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// Determine if a node is null to determine if a corresponding node is found
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// Delete node s according to their type
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
tab[index] = node.next;
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
5. Serialization and deserialization of HashMap
5.1 Serialization of HashMap
(1) The serialization functions of HashMap are as follows:
/**
* Save the state of the <tt>HashMap</tt> instance to a stream (i.e.,
* serialize it).
*
* @serialData The <i>capacity</i> of the HashMap (the length of the
* bucket array) is emitted (int), followed by the
* <i>size</i> (an int, the number of key-value
* mappings), followed by the key (Object) and value (Object)
* for each key-value mapping. The key-value mappings are
* emitted in no particular order.
*/
private void writeObject(java.io.ObjectOutputStream s)
throws IOException {
int buckets = capacity(); // Returns the capacity size of HashMap
// Write out the threshold, loadfactor, and any hidden stuff
s.defaultWriteObject();
s.writeInt(buckets);
s.writeInt(size); // size is the number of nodes in HashMap
internalWriteEntries(s);
}
(2) Serialization correlation function
- capacity function
// These methods are also used when serializing HashSets
final float loadFactor() { return loadFactor; }
final int capacity() {
return (table != null) ? table.length :
(threshold > 0) ? threshold :
DEFAULT_INITIAL_CAPACITY;
}
- InternaalWriteEntries function
// Called only from writeObject, to ensure compatible ordering.
void internalWriteEntries(java.io.ObjectOutputStream s) throws IOException {
Node<K,V>[] tab;
if (size > 0 && (tab = table) != null) {
// Traverse through each node in HashMap, writing the key and value of the node
// Node hash values are not written because they may be calculated differently by different JDK versions
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
s.writeObject(e.key);
s.writeObject(e.value);
}
}
}
}
5.2 Deserialization of HashMap
(1) The deserialization functions of HashMap are as follows:
/**
* Reconstitutes this map from a stream (that is, deserializes it).
* @param s the stream
* @throws ClassNotFoundException if the class of a serialized object
* could not be found
* @throws IOException if an I/O error occurs
*/
private void readObject(java.io.ObjectInputStream s)
throws IOException, ClassNotFoundException {
// Read in the threshold (ignored), loadfactor, and any hidden stuff
s.defaultReadObject();
reinitialize(); // Initialization
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new InvalidObjectException("Illegal load factor: " +
loadFactor);
s.readInt(); // Read and ignore number of buckets
int mappings = s.readInt(); // Read number of mappings (size)
if (mappings < 0)
throw new InvalidObjectException("Illegal mappings count: " +
mappings);
else if (mappings > 0) { // (if zero, use defaults)
// Size the table using given load factor only if within
// range of 0.25...4.0
// Calculate variables such as threshold s and cap s
float lf = Math.min(Math.max(0.25f, loadFactor), 4.0f);
float fc = (float)mappings / lf + 1.0f;
int cap = ((fc < DEFAULT_INITIAL_CAPACITY) ?
DEFAULT_INITIAL_CAPACITY :
(fc >= MAXIMUM_CAPACITY) ?
MAXIMUM_CAPACITY :
tableSizeFor((int)fc));
float ft = (float)cap * lf;
threshold = ((cap < MAXIMUM_CAPACITY && ft < MAXIMUM_CAPACITY) ?
(int)ft : Integer.MAX_VALUE);
// Check Map.Entry[].class since it's the nearest public type to
// what we're actually creating.
SharedSecrets.getJavaOISAccess().checkArray(s, Map.Entry[].class, cap);
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] tab = (Node<K,V>[])new Node[cap]; // Create Initialization Array
table = tab; // Assign to table
// Read the keys and values, and put the mappings in the HashMap
for (int i = 0; i < mappings; i++) { // Traverse all number nodes
// Call readObject to get key s and value s for all nodes
@SuppressWarnings("unchecked")
K key = (K) s.readObject();
@SuppressWarnings("unchecked")
V value = (V) s.readObject();
// Perform node insertion via putVal
putVal(hash(key), key, value, false, false);
}
}
}
(2) Deserialization correlation function
- reinitialize function
/**
* Reset to initial default state. Called by clone and readObject.
*/
void reinitialize() {
table = null;
entrySet = null;
keySet = null;
values = null;
modCount = 0;
threshold = 0;
size = 0;
}
3. Summary (Three Examination Points)
The first three summaries focus on
(1) The reason why the capacity of an array is a power of two:
- Increase the speed of operations (bitwise operations);
- Increase hash and decrease conflict ((n-1) &hash);
- Reduce memory fragmentation.
(2) hash function and hashcode calculation: the exclusive or operation (exclusive or operation with itself after moving 16 bits to the right) of hashcode increases randomness, thereby increasing hash and reducing conflicts
(3) Expansion:
- Conditions for capacity expansion: the actual number of nodes is more than three-quarters of the capacity;
- Data layout after expansion:
- Position of original subscript
- Position of original subscript + original capacity
(4) The data structure of hashmap includes initial array, chain table, red-black tree
(5) Insert conflict: Resolve the conflict through a single-chain table, and if the chain length exceeds 8 (TREEIFY_THRESHOLD = 8), convert the single-chain table to the red-black tree to improve query speed.
(6) Serialization: only the capacity of the array, the actual number of nodes, and the key/value of each node are stored
Reference material: