Breadth first traversal of Graphs

1, Introduction

1. breadth-first search
   Breadth first traversal starts from a vertex v, first accesses the node and marks it as visited, then sequentially accesses all the unreachable adjacency points {vi,..., vj} of node V and marks it as visited, and then repeats the access method of node V for each node in {vi,..., vj} until all nodes are accessed. There are three steps:

• Using a secondary queue, first put the first node v into the queue and mark that it is also accessed, and then detect whether the queue is empty
• If the queue is not empty, take out the first element of the queue, add the nodes connected to the node and not accessed to the queue, and mark these nodes
• When the queue is empty, the breadth first traversal of the graph is completed

1. Shortest path of graph
   The shortest path strength of an unauthorized graph is based on the breadth first traversal of the graph. It refers to the shortest path between two nodes in the graph, which is used to record the path from the previous node to node i through the ord[i] array

2, Traversal process

Let's take a look at specific examples:
Breadth first traversal of the following figure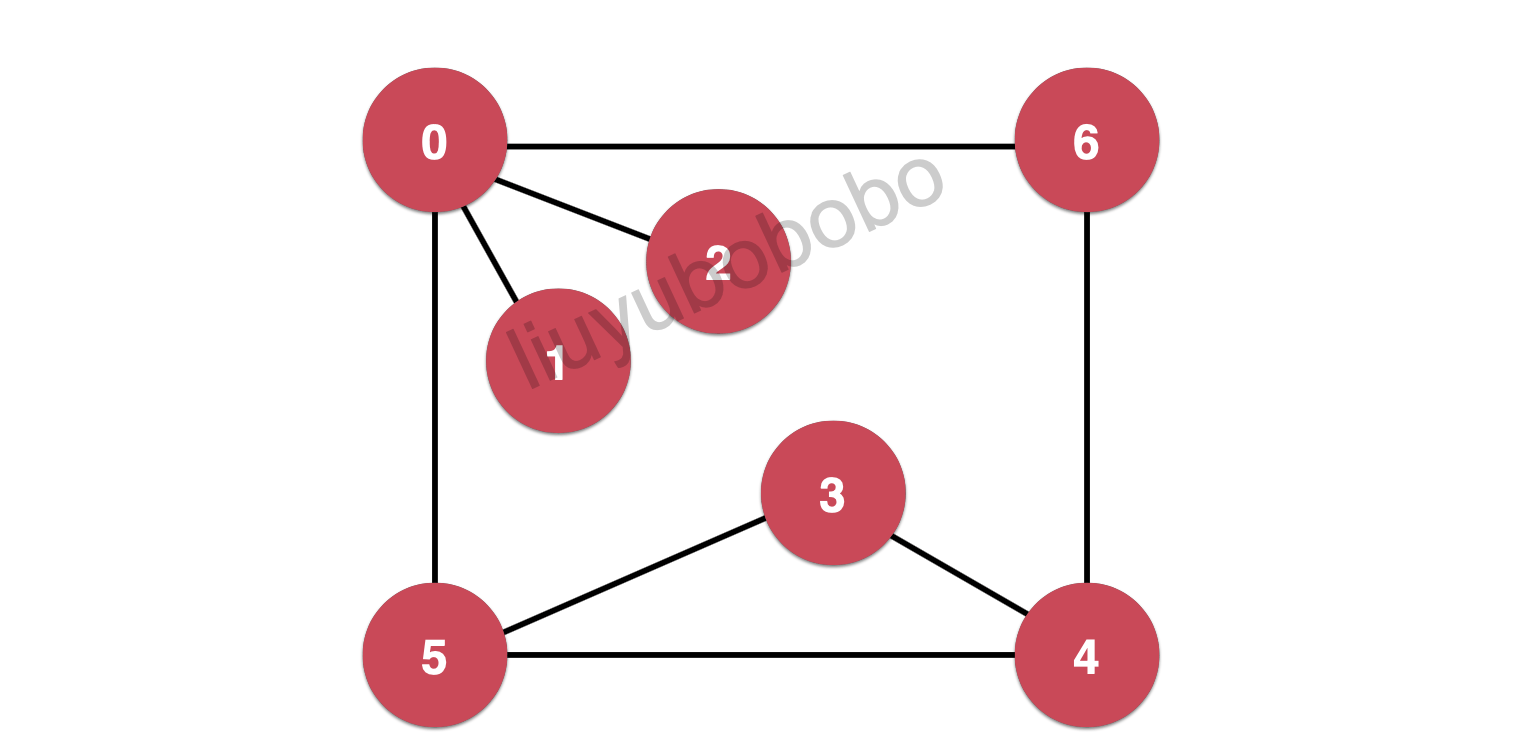

Starting from node 0
Put node 0 in the queue and mark it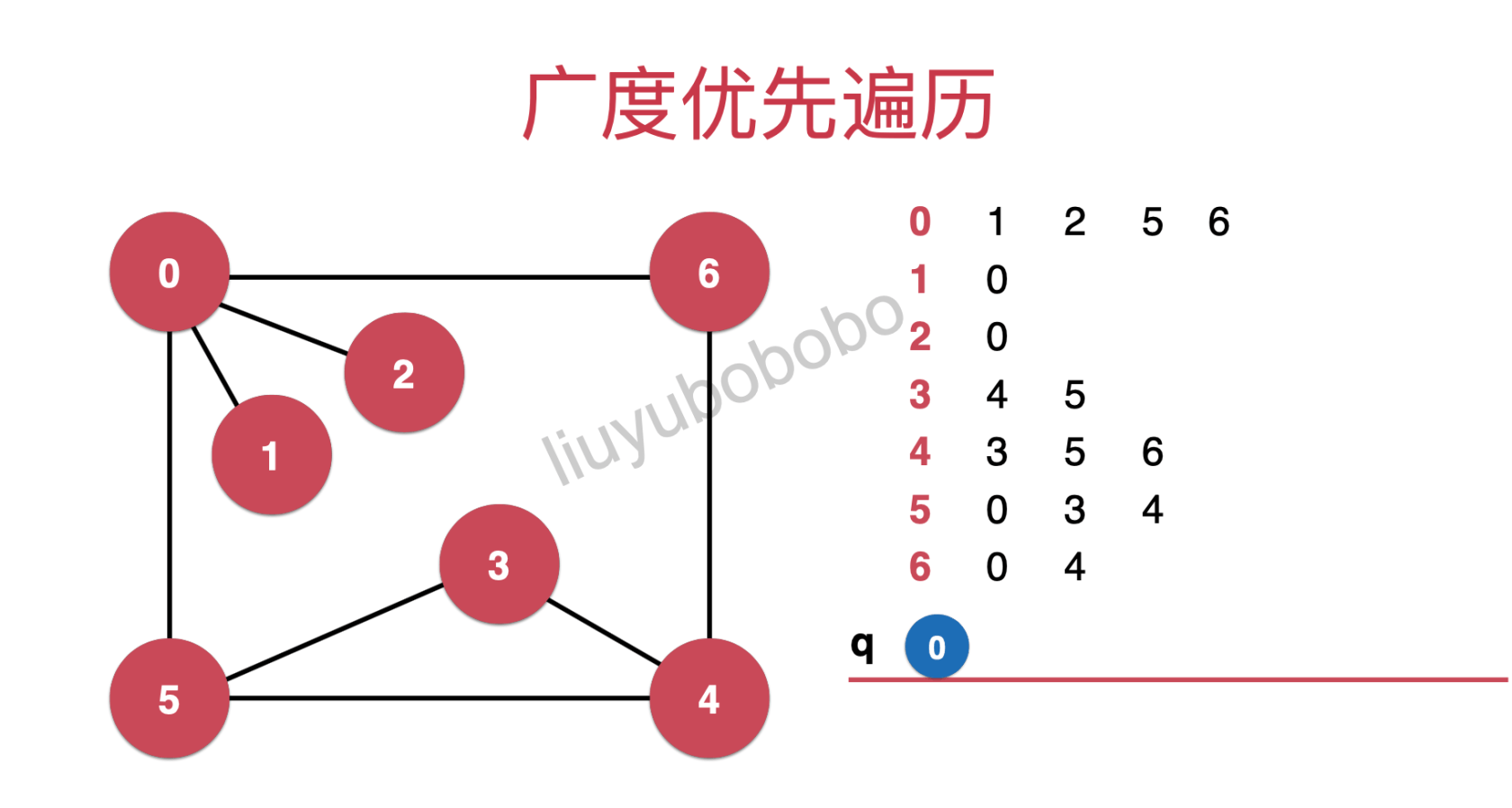

When the queue is not empty, take out the first element from the queue, that is, node 0; Then put the nodes connected to node 0 that have not been accessed in turn into the queue and mark them, as shown in the following figure: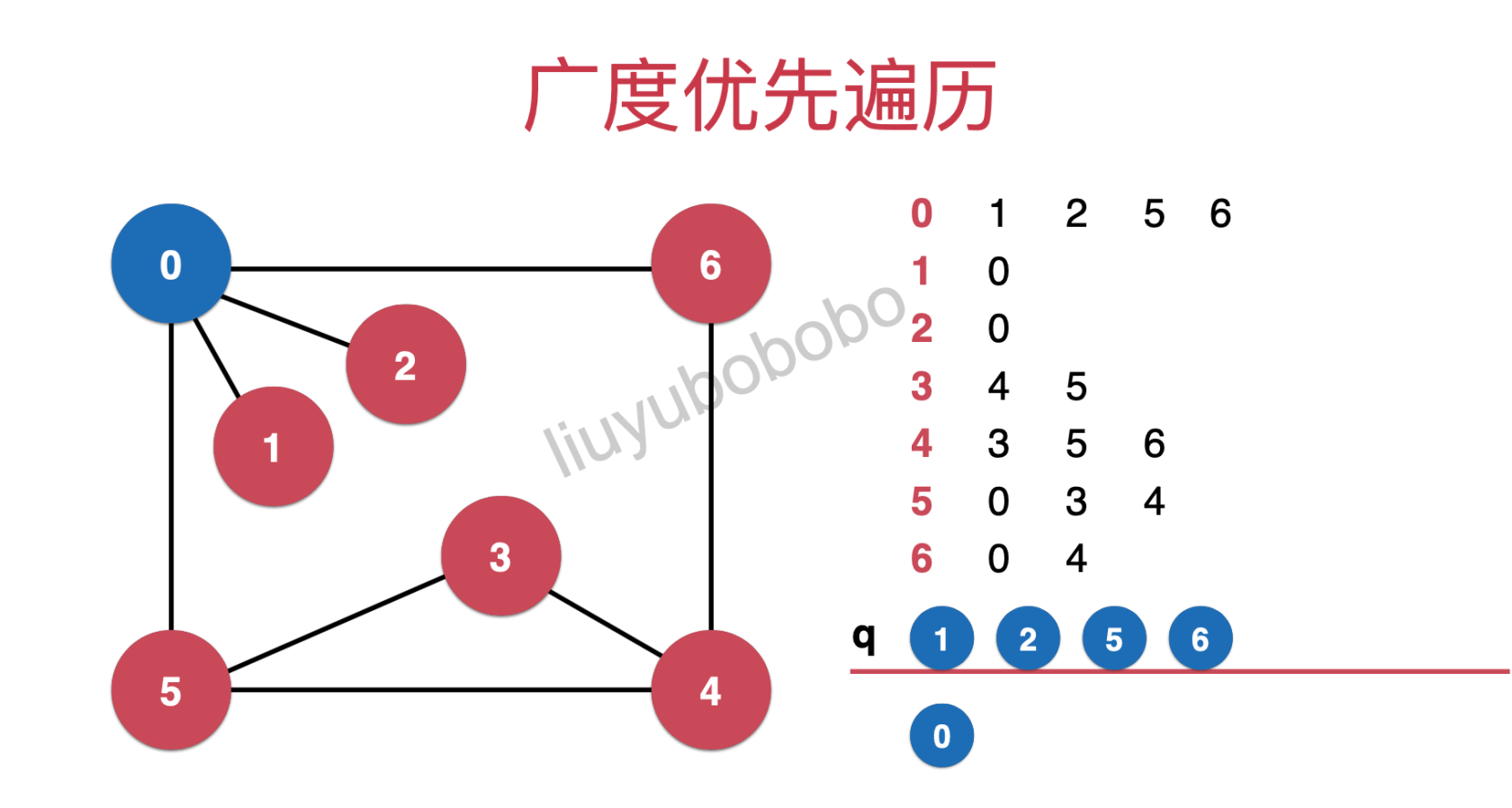

Similarly, if the queue is not empty, take out the first element node 1 in the queue. If there is no node connected to node 1 and has not been accessed, no node will enter the queue and then enter the next round of traversal.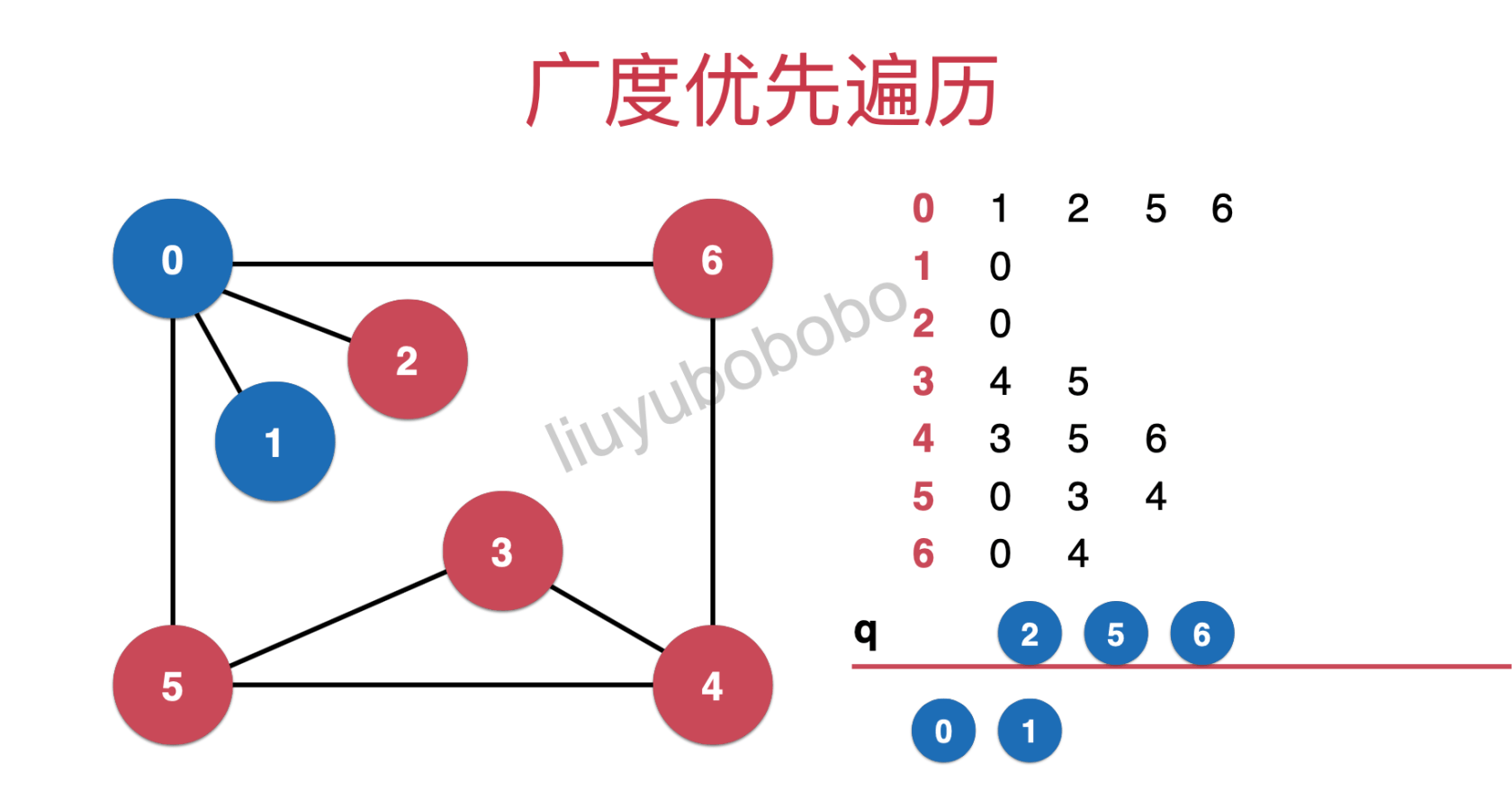

If the queue is not empty, take out the first element node 2 of the queue. Similarly (refer to the outgoing queue of node 1) and enter the next round of traversal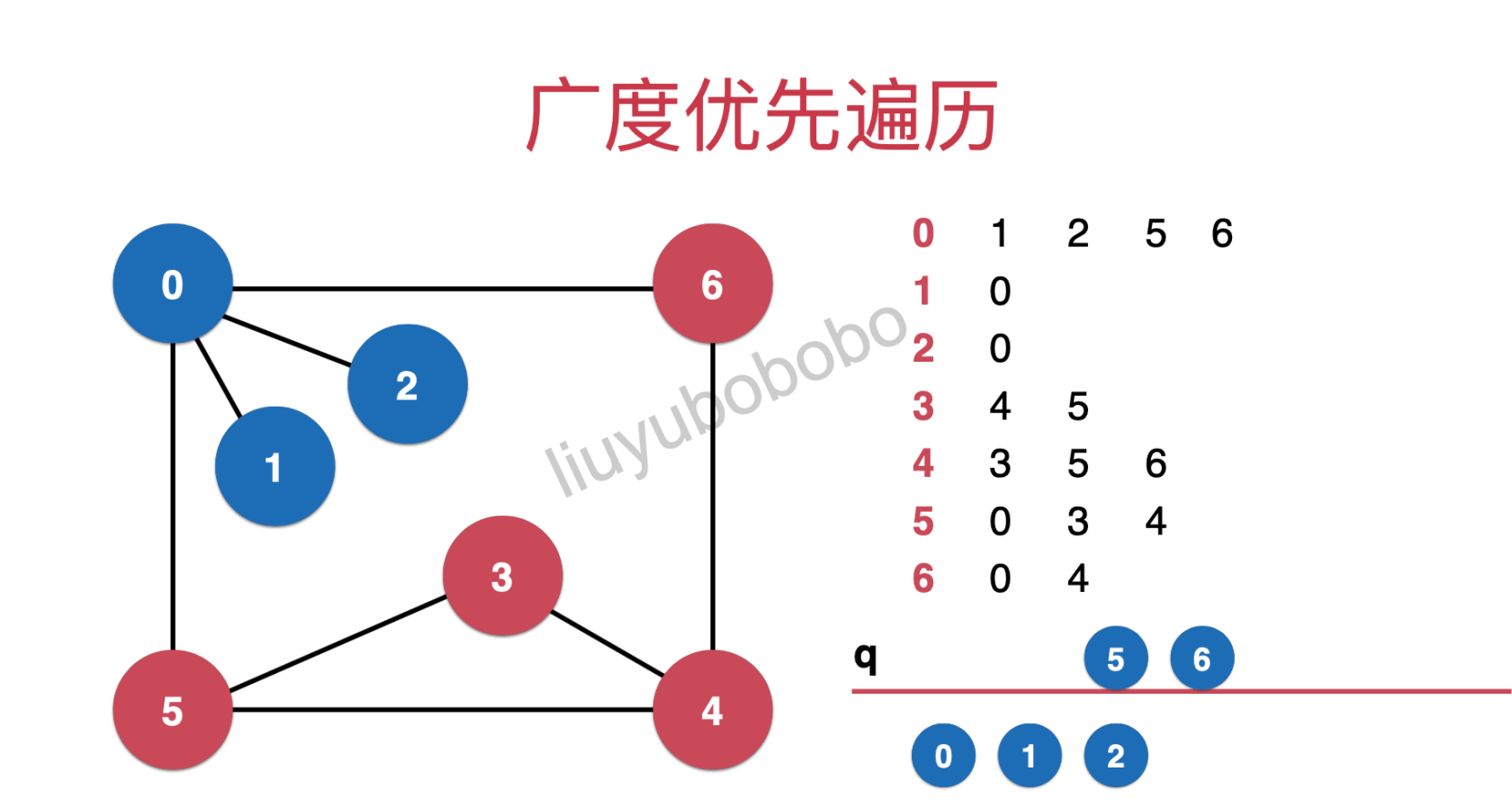

If the queue is not empty, take out the first element node 5 of the queue, put the node connected to 5 and not accessed into the queue and mark it, as shown in the following figure:

If the queue is not empty, take out the first element node 6 of the queue. At this time, the nodes connected to node 6 and not accessed are empty and enter the next round of traversal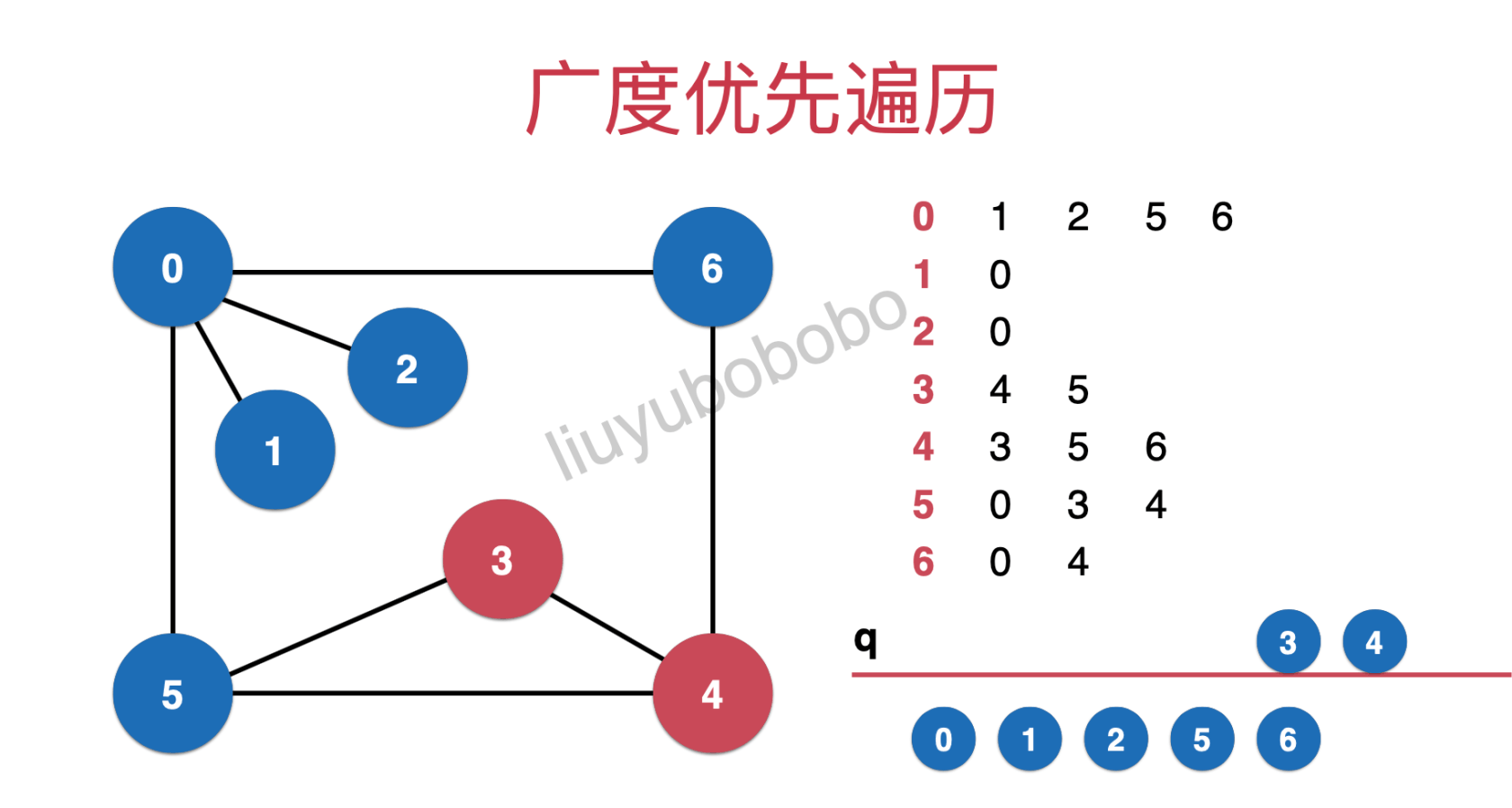

Similarly, traverse node 3: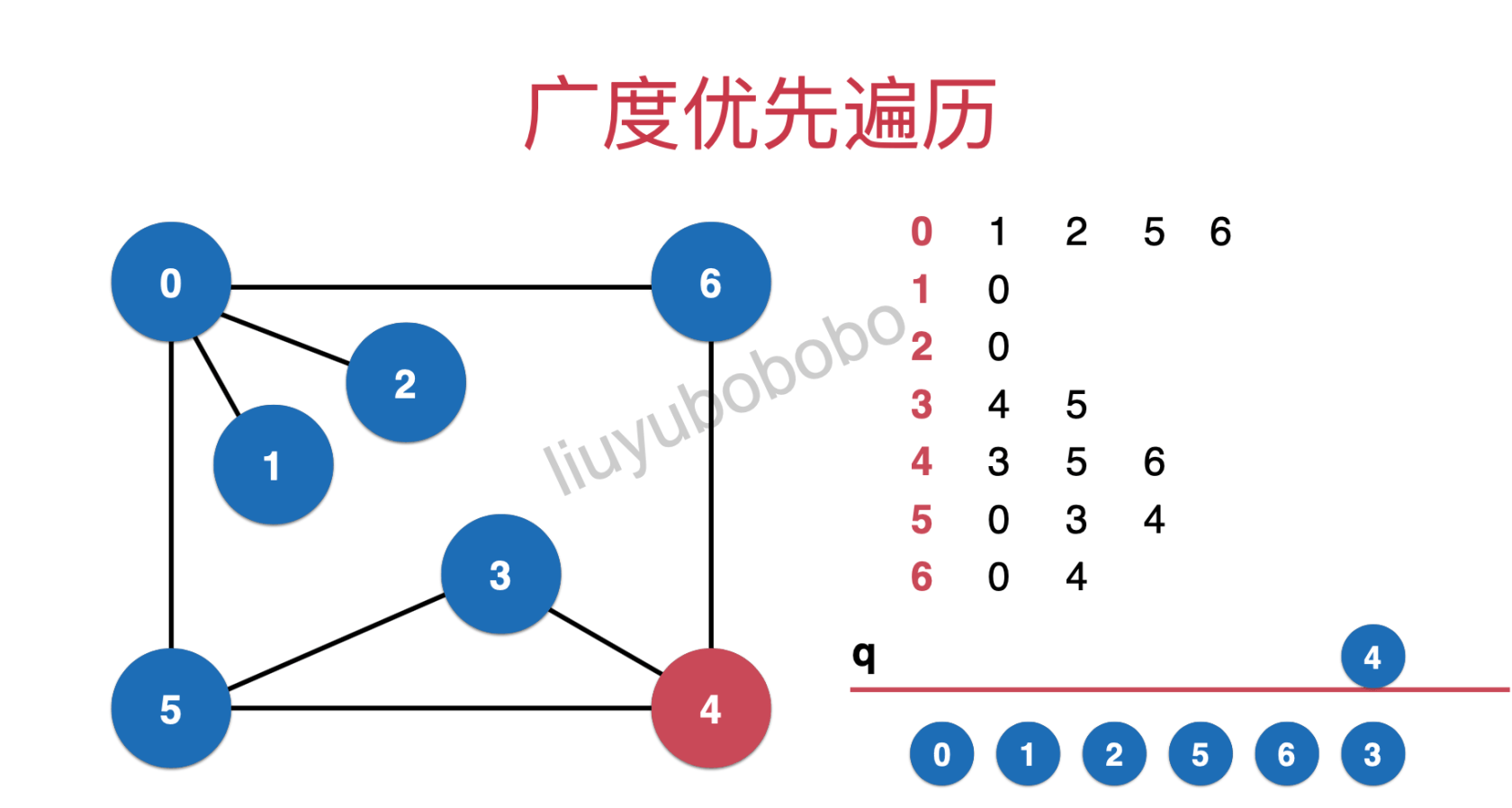

Similarly, traverse node 4; At this time, the queue is empty and the traversal is completed

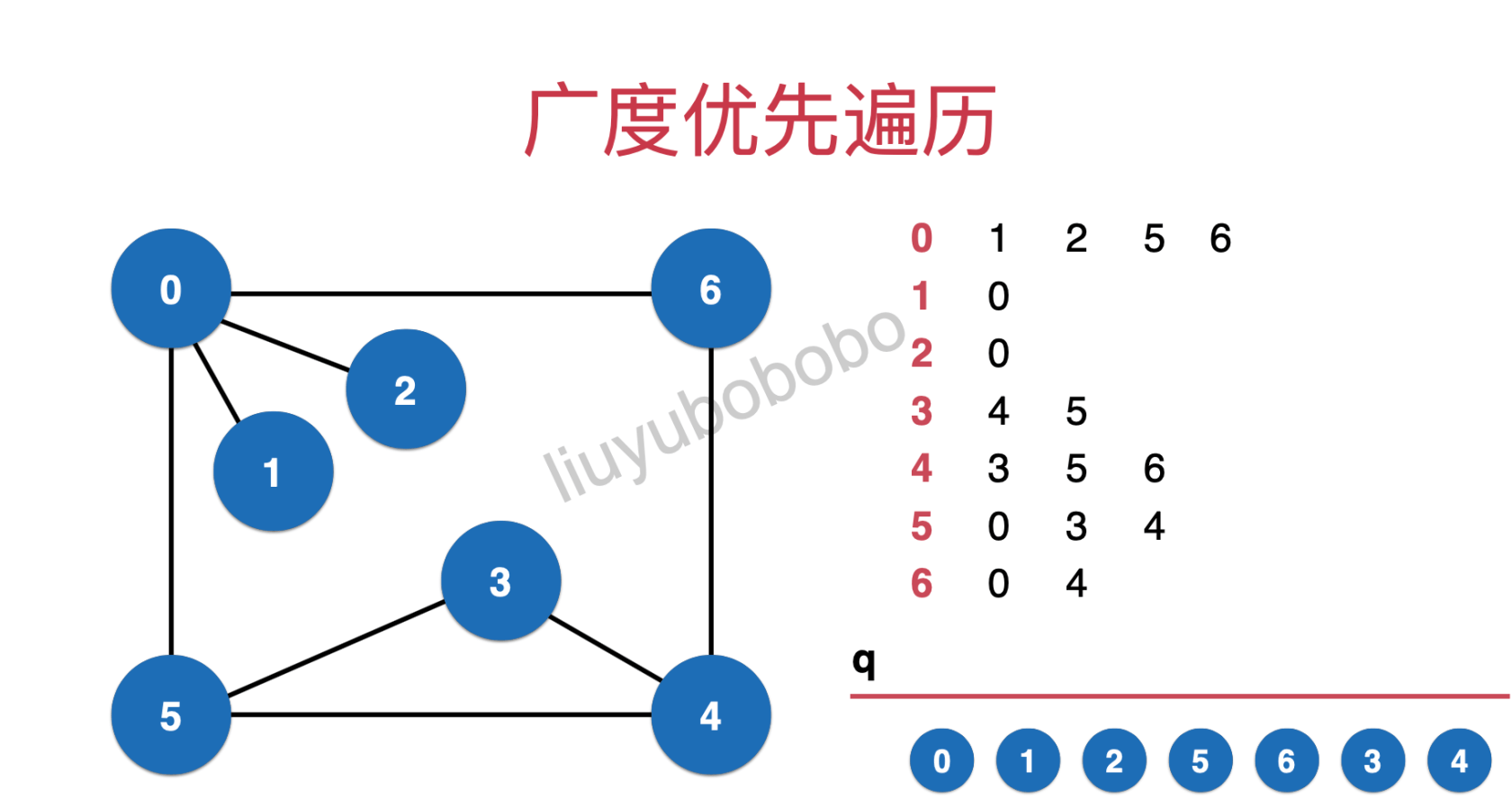
3, Code implementation

Write a class, member variable and its initialization:

#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <cassert>

using namespace std;

//Find the shortest path of the graph
template <typename Graph>   //Encapsulated as a unified interface
class ShortestPath{

private:
    Graph &G; //Graph is a reference
    int s; //starting point
    bool *visited; //Whether nodes are marked in the process of recording dfs
    int *from; //Record the path. from[i] represents the previous node of I on the query path
    int *ord; //Record the order of nodes in the path. ord[i] indicates the order of I nodes in the path

public:
    //Constructor
  ShortestPath(Graph &graph, int s):G(graph){

       //Algorithm initialization
       assert( s >= 0 && s < graph.V() );
       this->s = s;
       visited = new bool[graph.v()];
       from = new int[graph.v()];
       ord = new int[graph.v()];
       for(int i = 0; i < graph.v(); i++){
            visited[i] = false;
            from[i] = -1;
            ord[i] = -1;
  }

Breadth first traversal algorithm:

// The shortest path algorithm of undirected graph traverses the whole graph in breadth first from s
  queue<int> q;    //q is the auxiliary queue

  q.push( s );
  visited[s] = true;
  ord[s] = 0;
  while( !q.empty() ){
        //Assign the first element in the queue to v
        int v = q.front();
        q.pop(); //Take the first element out of the queue

        typename Graph::adjIterator adj(G, v);
        for( int i = adj.begin(); !adj.end(); i = adj.next() ){
                if( !visited[i] ){    //Judge whether the node has been accessed
                    q.push(i);
                    visited[i] = true;
                    from[i] = v;
                    ord[i]  = ord[v] + 1;      //Record shortest path
                }
         }
    }
}

Destructor and its member functions

//Destructor
  ~ShortestPath(){
        delete[] visited;
        delete[] from;
        delete[] ord;
  }
    // Query whether there is a path from point s to point w
  bool hasPath(int w) {
        assert(w >= 0 && w < G.V());
        return visited[w];
  }

   // Query the path from point s to point w and store it in vec
  void path(int w,vector<int> vec){
        assert(w >= 0 && w < G.V());
        stack<int> s;
        // Reverse search the path from s to w through the from array and store it in the stack
        int p = w;
        while(p != -1){
            s.push(p);
            p = from[p];
        }

        // Take out the elements from the stack in turn to obtain the sequential path from s to w
       vec.clear();
       while( !s.empty() ){
                vec.push_back( s.top());
                s.pop();
       }
    }

    // Print the path from point s to point w
  void showPath(int w){

        assert( w >= 0 && w < G.V() );

        vector<int> vec;
        path(w, vec);
        for( int i = 0 ; i < vec.size() ; i ++ ){
                cout<<vec[i];
              if( i == vec.size()-1 )
                    cout<<endl;
              else  cout<<" -> ";
       }
    }

    // View the shortest path length from point s to point w
  int length(int w){
        assert( w >= 0 && w < G.V() );
        return ord[w];
  }
};