preface
Today, I will summarize the sorting algorithm often asked in the school recruitment interview. If you think the article is good, I hope you can like it and see it again. Thank you! There are benefits at the end of the article. Remember to check it~
Pre knowledge
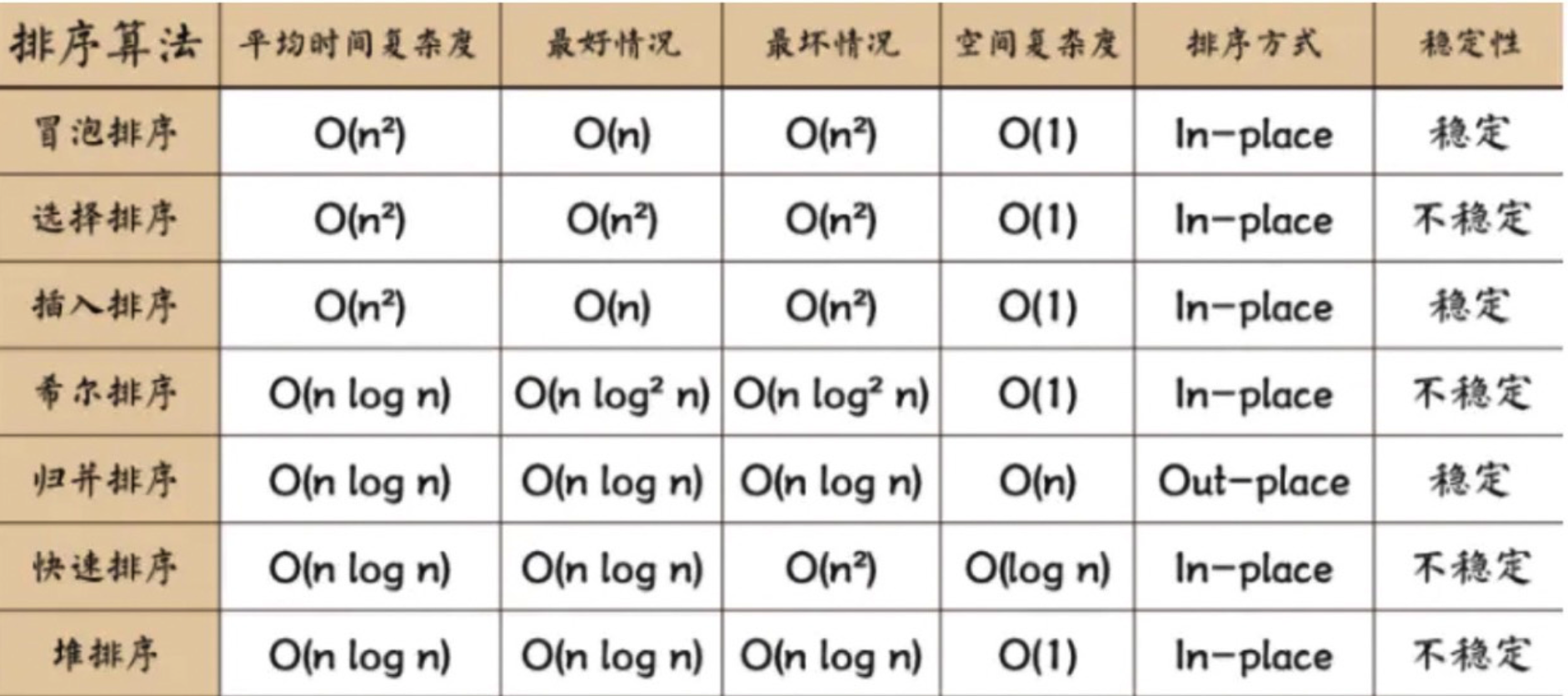
Stability of sorting algorithm
The stability of the sorting algorithm refers to whether the front and rear positions of the two elements have changed after sorting when the values of two elements in the input elements are the same.
Application scenario
1. Order sorting
Suppose you need to display orders for users in chronological order, and orders at the same time point are displayed in order of order amount.
In terms of implementation, you can first arrange the order by order amount, and then arrange the order by time.
Then, the stability of the sorting algorithm here reflects its potential
Assuming that sorting by time is not stable, two orders at the same time may be sent for order exchange, thus undermining the previous results sorted by amount.
Conclusion: sort by order amount first, and then sort by time with stable sorting algorithm.
2. Ranking of scores
Suppose you need to sort the students' paper scores, and the students with the same scores are sorted according to their usual scores.
In terms of implementation, with the experience of the first example, we already know that we should first sort according to the usual score, and then sort according to the score of the volume with a stable sorting algorithm.
Because if you encounter students with the same score, the unstable ranking will destroy the normal score.
- Internal sorting: all sorting operations are completed in memory;
- External sorting: because the data is too large, the data is placed on the disk, and the sorting can only be carried out through the data transmission of disk and memory; Time complexity: the time spent in the execution of an algorithm.
- Space complexity: the amount of memory required to run a program.
A picture
Bubble sorting
Core idea:
Compare the two adjacent numbers in turn, and put the decimal number in the front and the large number in the back.
In the first trip: first compare the first and second numbers, put the decimal before and the large number after. Then compare the second number and the third number, put the decimal before and after the large number, and continue until the last two numbers are compared, put the decimal before and after the large number. So far, the first trip is over, and the maximum number is put to the last.
In the second round: still start the comparison from the first logarithm (because the exchange of the second number and the third number may make the first number no longer less than the second number), put the decimal before, put the large number after, and compare to the penultimate number (the penultimate position is already the largest), and the second round ends, Get a new maximum number in the penultimate position (in fact, it is the second largest number in the whole sequence).
If so, repeat the above process until the sorting is finally completed.
For example: 4 5 6 3 2 1, sort from small to large
The result of the first bubbling: 4 5 6 3 2 1 - > 4 5 3 6 2 1 - > 4 5 3 2 6 1 - > 4 5 3 2 1 6, 6 the position of this element is determined
The result of the second bubbling: 4 5 3 2 1 6 - > 4 3 5 2 1 6 - > 4 3 2 5 1 6 - > 4 3 2 1 5 6, 5 the position of this element is determined
The result of the third bubbling: 4 3 2 1 5 6 - > 3 4 2 1 5 6 - > 3 2 4 1 5 6 - > 3 2 1 4 5 6, 4 the position of this element is determined
The result of the fourth bubbling: 3 2 1 4 5 6 - > 2 3 1 4 5 6 - > 2 1 3 4 5 6, 3 the position of this element is determined
The result of the fifth bubbling: 2 1 3 4 5 6 - > 1 2 3 4 5 6, 2 the position of this element is determined

realization
Set the array length to N:
1. Compare the two adjacent data. If the previous data is greater than the later data, exchange the two data.
2. After traversing from the 0th data to the n-1st data of the array, the largest data will "sink" to the n-1st position of the array.
3. Cycle N=N-1. If N is not 0, repeat the previous two steps, otherwise the sorting is completed.
public class BubbleSort {
public static void BubbleSort(int[] arr) {
int temp;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j + 1] < arr[j]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int arr[] = new int[]{1, 6, 2, 3, 22};
BubbleSort.BubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
}
Shortcomings of bubble sorting method and its improvement
In the sorting process, after the final sorting, although the data has been sorted completely, the program cannot judge whether the sorting is completed. In order to solve this problem, set a flag bit flag and set its initial value to non-0, indicating that the sorted table is an unordered table. Set the flag value to 0 before each sorting. During data exchange, Modify the flag to non-0.
At the beginning of a new round of sorting, check this flag. If this flag is 0, it means that no data exchange has been done last time (ordered state), then the sorting is ended; Otherwise, sort;
optimization
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int data[] = { 4, 5, 6, 3, 2, 1 };
int n = data.length;
for (int i = 0; i < n - 1; i++) { //Number of times to sort
boolean flag = false;
for (int j = 0; j < n - 1 - i; j++) { //I - specific bubbling
if (data[j] > data[j + 1]) {
int temp = data[j];
data[j] = data[j + 1];
data[j + 1] = temp;
flag = true;
}
}
if(!flag) break;
}
System.out.println(Arrays.toString(data));
}
}
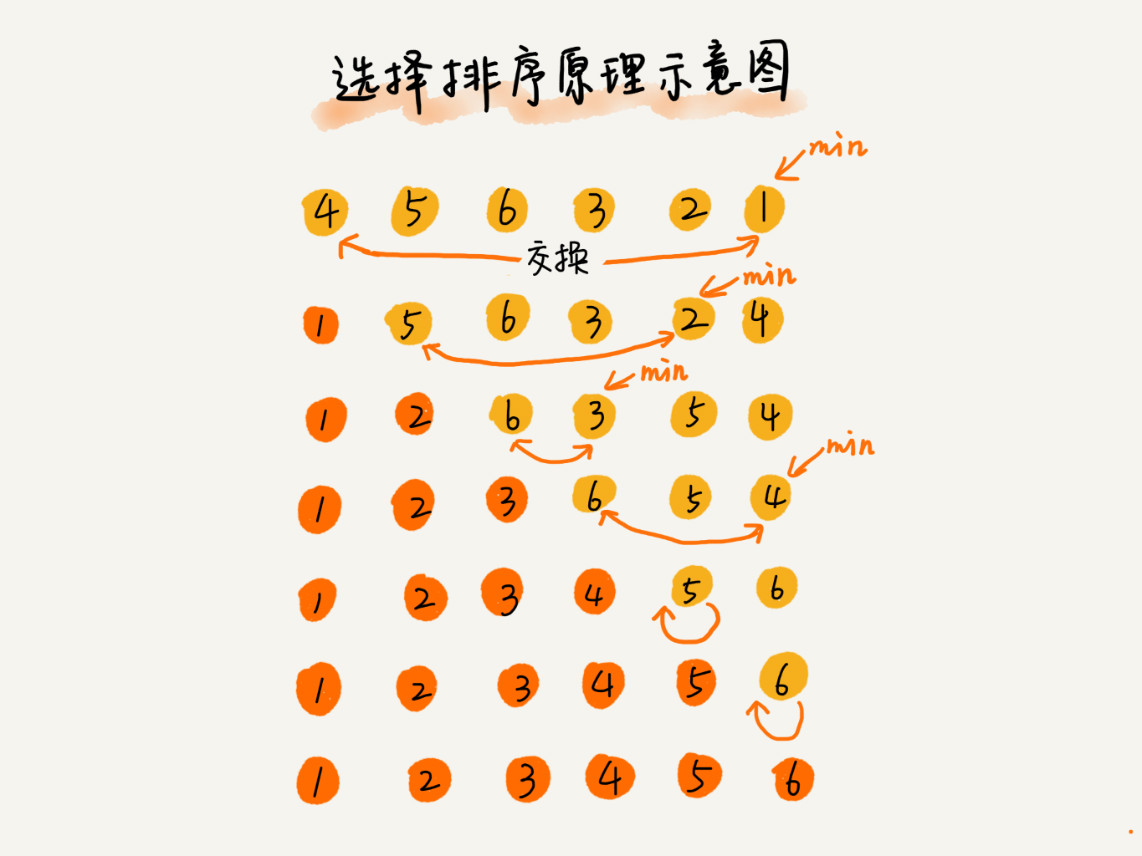
Select sort
First, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorting sequence, then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence, and so on until all elements are sorted
Due to the existence of data exchange, selective sorting is not a stable sorting algorithm
realization
public class SelectionSort {
public int[] selectionSort(int[] A, int n) {
//Record minimum subscript value
int min=0;
for(int i=0; i<A.length-1;i++){
min = i;
//Find the minimum value after the beginning of subscript i
for(int j=i+1;j<A.length;j++){
if(A[min]>A[j]){
min = j;
}
}
if(i!=min){
swap(A,i,min);
}
}
return A;
}
private void swap(int[] A,int i,int j){
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
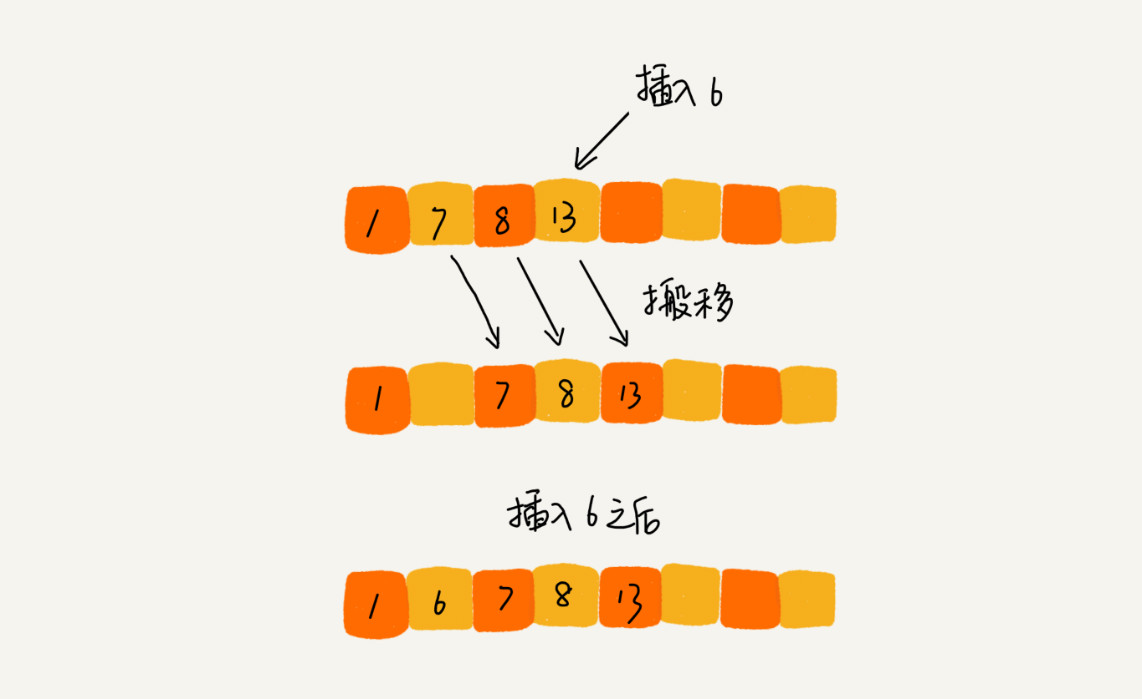
Insert sort
The working principle of the insertion sorting algorithm is to construct an ordered sequence. For the unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert it. Therefore, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements backward step by step to provide insertion space for the latest elements
realization
public class InsertionSort {
public int[] insertionSort(int[] A, int n) {
//The idea of inserting playing cards with simulation
//Inserted playing cards
int i,j,temp;
//One has been inserted, continue to insert
for(i=1;i<n;i++){
temp = A[i];
//Move all the cards in front of i that are larger than the card to be inserted back one bit, and leave one for the new card
for(j=i;j>0&&A[j-1]>temp;j--){
A[j] = A[j-1];
}
//Fill the empty one with the inserted card
A[j] = temp;
}
return A;
}
}
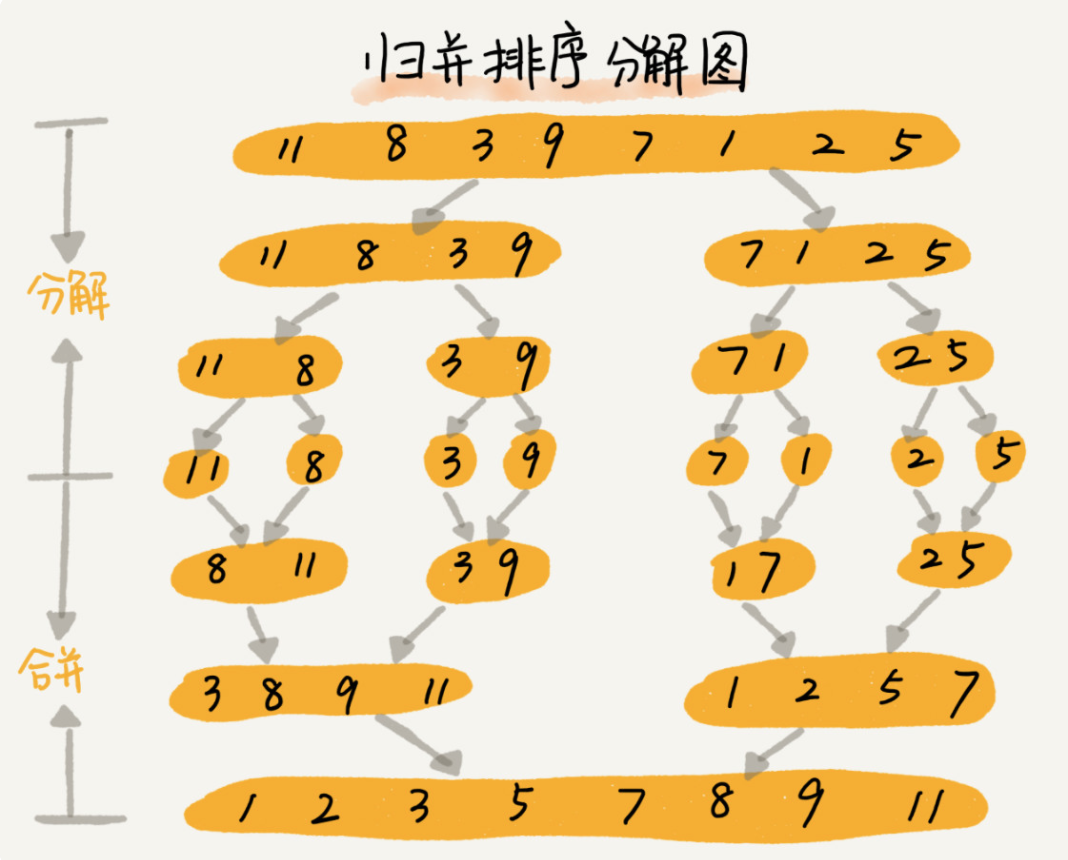
Merge sort
The core of merging and sorting is the idea of divide and conquer. First divide the array into the front and back parts from the middle, then sort the front and back parts respectively, and then merge the two parts in good order, so that the whole array is in order
If two ordered tables are merged into one, it is called two-way merging
Merge sort is a stable sort algorithm
realization
public class MergeSort {
public static void main(String[] args) {
int data[] = { 9, 5, 6, 8, 0, 3, 7, 1 };
megerSort(data, 0, data.length - 1);
System.out.println(Arrays.toString(data));
}
public static void mergeSort(int data[], int left, int right) { // Both ends of the array
if (left < right) { // Equal means that there is only one number and there is no need to dismantle it
int mid = (left + right) / 2;
mergeSort(data, left, mid);
mergeSort(data, mid + 1, right);
// After the division, we need to merge, that is, the process of recursive internal return
merge(data, left, mid, right);
}
}
public static void merge(int data[], int left, int mid, int right) {
int temp[] = new int[data.length]; //A temporary array is used to hold the merged data
int point1 = left; //Indicates the position of the first number on the left
int point2 = mid + 1; //Indicates the position of the first number on the right
int loc = left; //It means where we are now
while(point1 <= mid && point2 <= right){
if(data[point1] < data[point2]){
temp[loc] = data[point1];
point1 ++ ;
loc ++ ;
}else{
temp[loc] = data[point2];
point2 ++;
loc ++ ;
}
}
while(point1 <= mid){
temp[loc ++] = data[point1 ++];
}
while(point2 <= right){
temp[loc ++] = data[point2 ++];
}
for(int i = left ; i <= right ; i++){
data[i] = temp[i];
}
}
}
Shell Sort
Basic idea:
The algorithm first divides a group of numbers to be sorted into several groups according to a certain increment D (n/2, n is the number of numbers to be sorted), and the subscript difference of records in each group is d. all elements in each group are directly inserted and sorted, and then it is grouped with a smaller increment (d/2), and then directly inserted and sorted in each group. When the increment is reduced to 1, the sorting is completed after direct insertion sorting
Hill sort method (reduced increment method) belongs to insertion sort. It is a method to divide the whole non sequence into several small subsequences for insertion sort respectively
If the length of the array is 10, the array elements are 25, 19, 6, 58, 34, 10, 7, 98, 160 and 0
The algorithm process of hill sorting is as follows:
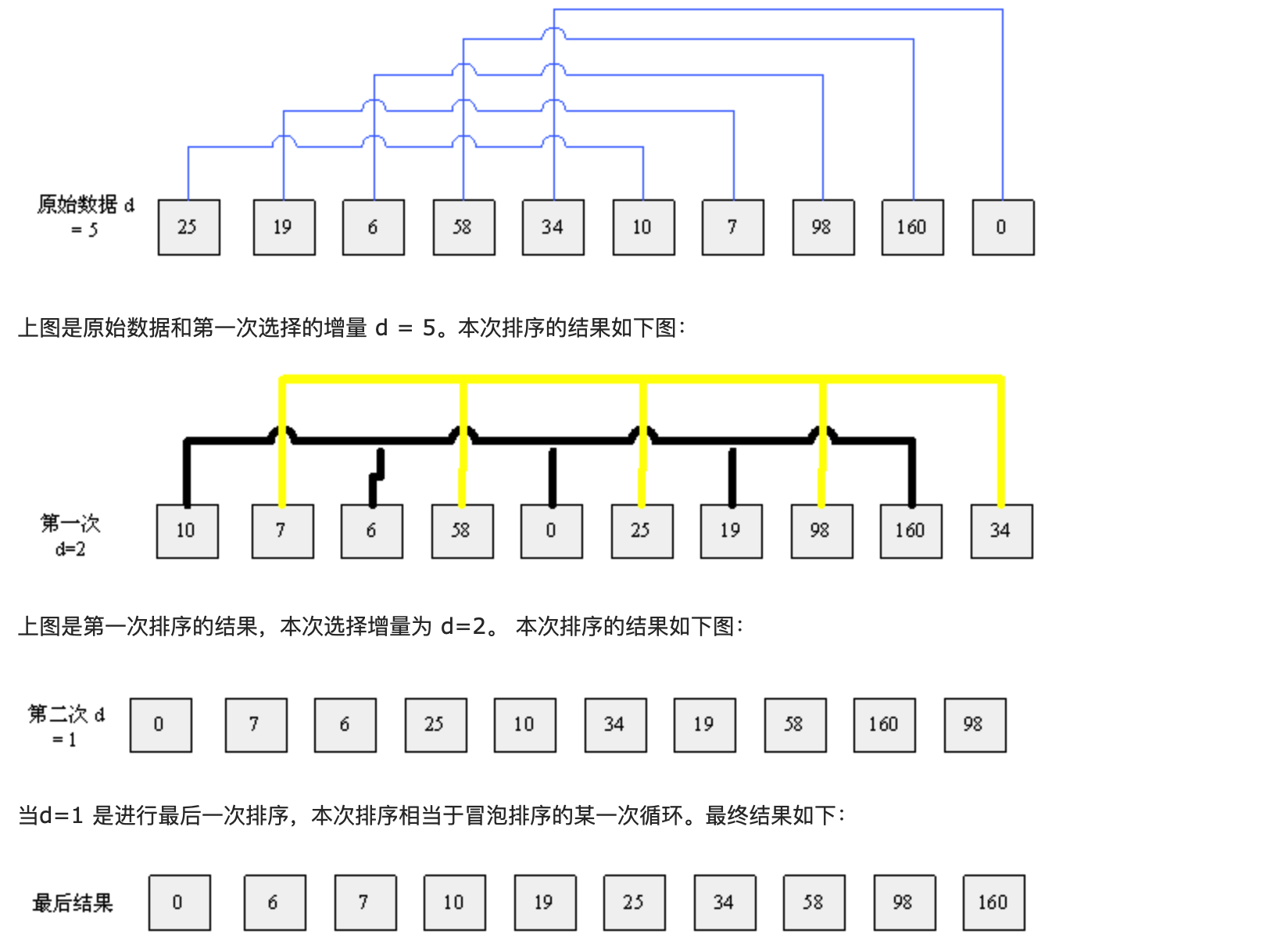
realization
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}
Quick sort
Basic idea of quick sort: divide the records to be arranged into two independent parts through one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the records of these two parts can be sorted separately to achieve the order of the whole sequence
- First, take a number from the sequence as the reference number.
- In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left.
- Repeat the second step for the left and right intervals until there is only one number in each interval.

Implementation 1
public class QuickSort {
public static void quickSort(int[]arr,int low,int high){
if (low < high) {
int middle = getMiddle(arr, low, high);
quickSort(arr, low, middle - 1);//Recursive left
quickSort(arr, middle + 1, high);//Recursive right
}
}
public static int getMiddle(int[] list, int low, int high) {
int tmp = list[low];
while (low < high) {
while (low < high && list[high] >= tmp) {//Larger than the keyword is on the right
high--;
}
list[low] = list[high];//If it is less than the keyword, switch to the left
while (low < high && list[low] <= tmp) {//Less than the keyword is on the left
low++;
}
list[high] = list[low];//If it is greater than the keyword, switch to the left
}
list[low] = tmp;
return low;
}
}
Implementation 2
public class QuickSort {
public static void quickSort(int data[], int left, int right) {
int base = data[left]; // Benchmark number, take the first in the sequence
int ll = left; // It shows the position from the left
int rr = right; // Indicates the position to find from the right
while (ll < rr) {
// Look for a number smaller than the benchmark number from the back
while (ll < rr && data[rr] >= base) {
rr--;
}
if (ll < rr) { // It means finding something bigger than it
int temp = data[rr];
data[rr] = data[ll];
data[ll] = temp;
ll++;
}
while (ll < rr && data[ll] <= base) {
ll++;
}
if (ll < rr) {
int temp = data[rr];
data[rr] = data[ll];
data[ll] = temp;
rr--;
}
}
// It must be that recursion is divided into three parts. Continue to quickly arrange left and right. Pay attention to adding conditions, otherwise recursion will overflow the stack
if (left < ll)
quickSort(data, left, ll - 1);
if (ll < right)
quickSort(data, ll + 1, right);
}
}
optimization
Basic quick sort selects the first or last element as the benchmark. However, this has been a very bad way to deal with it
If the array is already in order, the segmentation at this time is a very bad segmentation. Because each division can only reduce the sequence to be sorted by one, this is the worst case, and the quick sort is reduced to bubble sort, with a time complexity of O(n^2)
Triple median
The general practice is to use the median of the three elements at the left end, right end and center position as the hub element
For example, the sequence to be sorted is 8 1 4 9 6 3 5 2 7 0
8 on the left, 0 on the right and 6 in the middle
After we sort the three numbers here, the middle number is used as the pivot, and the pivot is 6
Insert sort
When the length of the sequence to be sorted is divided to a certain size, insert sorting is used. Reason: for small and partially ordered arrays, it is better to arrange quickly than to arrange well. When the length of the sequence to be sorted is divided to a certain size, the efficiency of continuous segmentation is worse than that of insertion sorting. At this time, interpolation can be used instead of fast sorting
Repeating array
After one split, you can gather the elements equal to the key together. When you continue the next split, you don't need to split the elements equal to the key
After a partition, the elements equal to the key are gathered together, which can reduce the number of iterations and improve the efficiency
Specific process: there are two steps in the processing process
The first step is to put the elements equal to key into both ends of the array during the partition process
The second step is to move the element equal to the key around the pivot after the division
give an example:
Sequence to be sorted 1 4 6 7 6 6 7 6 8 6
Select the pivot from the three numbers: the number 6 with subscript 4
After conversion, the sequence to be divided: 6 4 6 7 1 6 7 6 8 6
Pivot key: 6
The first step is to put the elements equal to key into both ends of the array during the partition process
The result is: 6 4 1 6 (pivot) 7 8 7 6 6 6
At this point, all elements equal to 6 are placed at both ends
The second step is to move the element equal to the key around the pivot after the division
The result is: 1 4 6 6 6 (pivot) 6 6 6 7 8 7
At this point, all elements equal to 6 are moved around the pivot
After that, fast sorting was performed in two subsequences: 1,4 and 7,8,7
Heap sort
Heap is a special kind of tree. As long as these two points are met, it is a heap.
- Heap is a complete binary tree;
- The value of each node in the heap must be greater than or equal to (or less than or equal to) the value of each node in its subtree.
The heap whose value of each node is greater than or equal to the value of each node in the subtree is called "big top heap".
The heap whose value of each node is less than or equal to the value of each node in the subtree is called "small top heap".
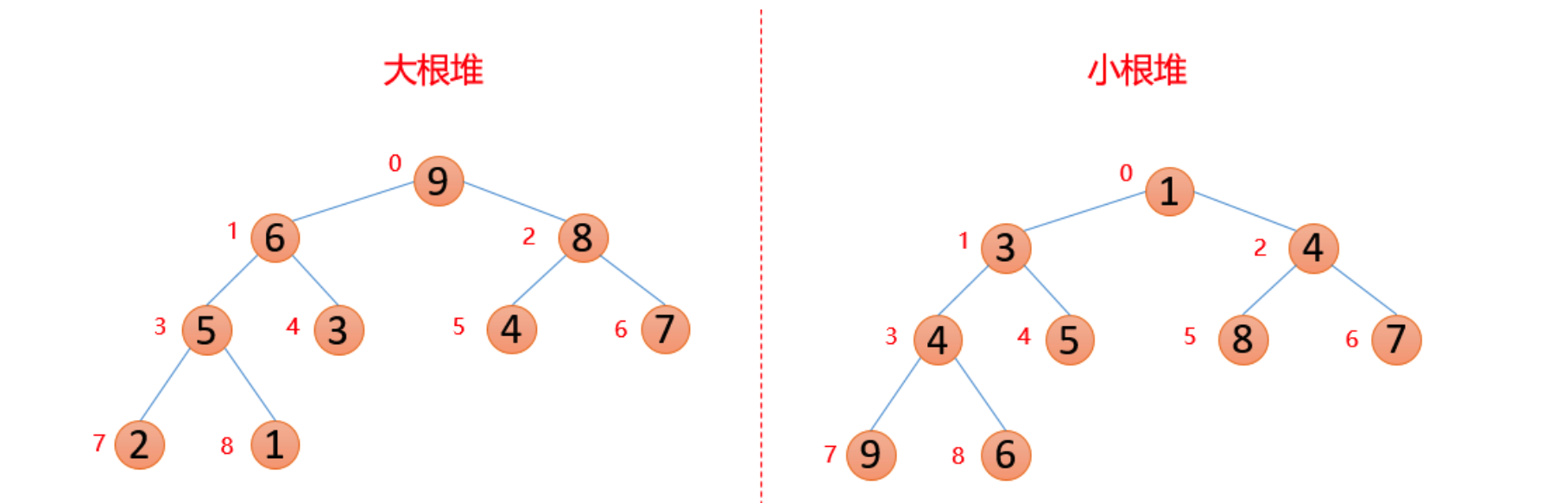
Generally, large root piles are used in ascending order and small root piles are used in descending order
How to implement a heap
Complete binary tree is more suitable for storing with array. Using arrays to store complete binary trees is very space efficient. Because we do not need to store the pointers of the left and right child nodes, we can find the left and right child nodes and parent nodes of a node simply through the subscript of the array.
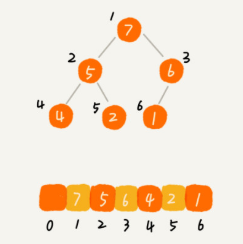
For example, find the parent node and left and right child nodes of a number in the array arr, such as the number with known index i
- Parent node index: (i-1)/2 (here, divide by 2 in the computer and omit the decimal)
- Left child index: 2*i+1
- Right child index: 2*i+2
Therefore, the definition and nature of heap:
- Large root pile: arr (I) > arr (2 * I + 1) & & arr (I) > arr (2 * I + 2)
- Small root pile: arr (I) < arr (2 * I + 1) & & arr (I) < arr (2 * I + 2)
Basic steps of heap sorting
1. First, construct the array to be sorted into a large root heap. At this time, the maximum value of the whole array is the top of the heap structure
2. Exchange the number at the top with the number at the end. At this time, the number at the end is the maximum and the number of remaining arrays to be sorted is n-1
3. Reconstruct the remaining n-1 numbers into a large root heap, and then exchange the top number with the number at n-1 position. In this way, an ordered array can be obtained
In the following, the data structure conversion of large top heap will be carried out for array arr[1,2,5,4,3,7].
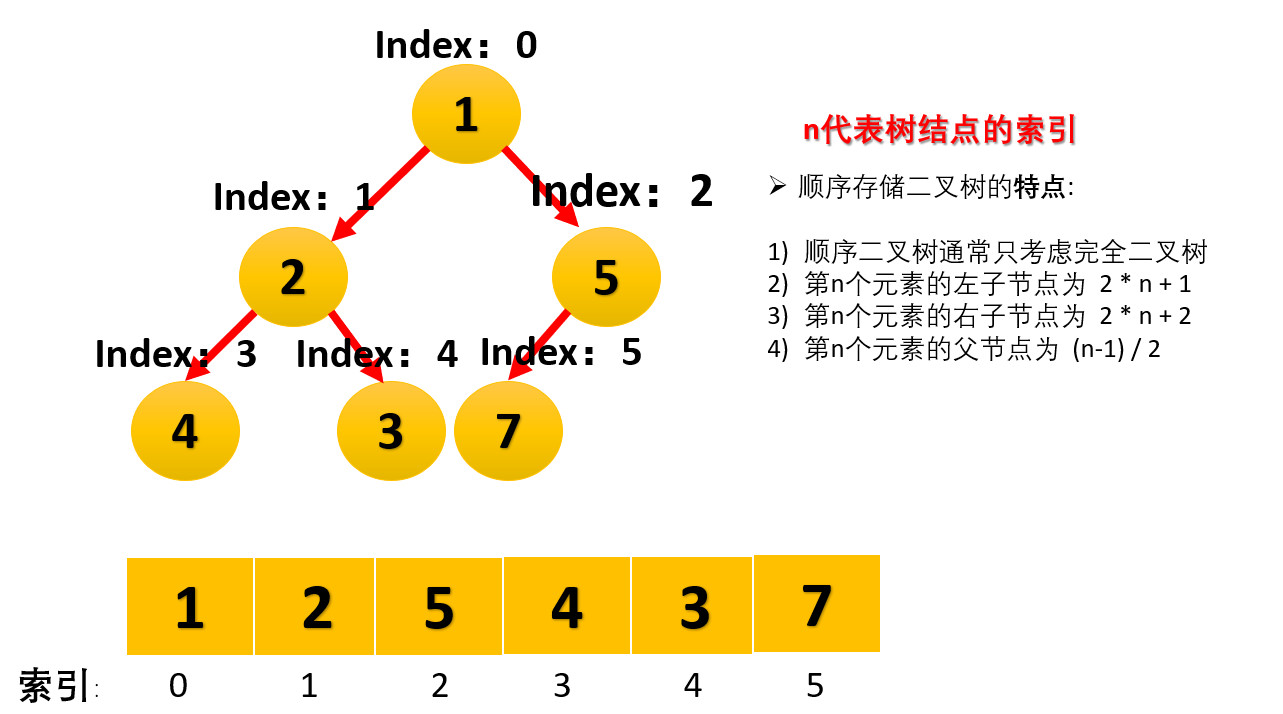
- We start with the last non leaf node (the first non leaf node arr.length/2-1=5/2-1=1, that is, the node with index 2), and adjust it from right to left and from bottom to top
- Since 7 elements in [5,7] are the largest, 5 and 7 are exchanged.
- The index of the last non leaf node is reduced by 1, and the second non leaf node (index 1) is found. Since the 4 elements in [4,3,2] are the largest, 2 and 4 are exchanged.
- The index of non leaf node is subtracted by 1, and the third non leaf node (index 0) is found. Since the 7 elements in [4,1,7] are the largest, 1 and 7 are exchanged.
- At this time, the exchange leads to the confusion of the structure of the sub root [1,5]. Continue to adjust. 5 is the largest in [1,5], and exchange 1 and 5.
- At this point, we construct a disordered sequence into a large top heap.
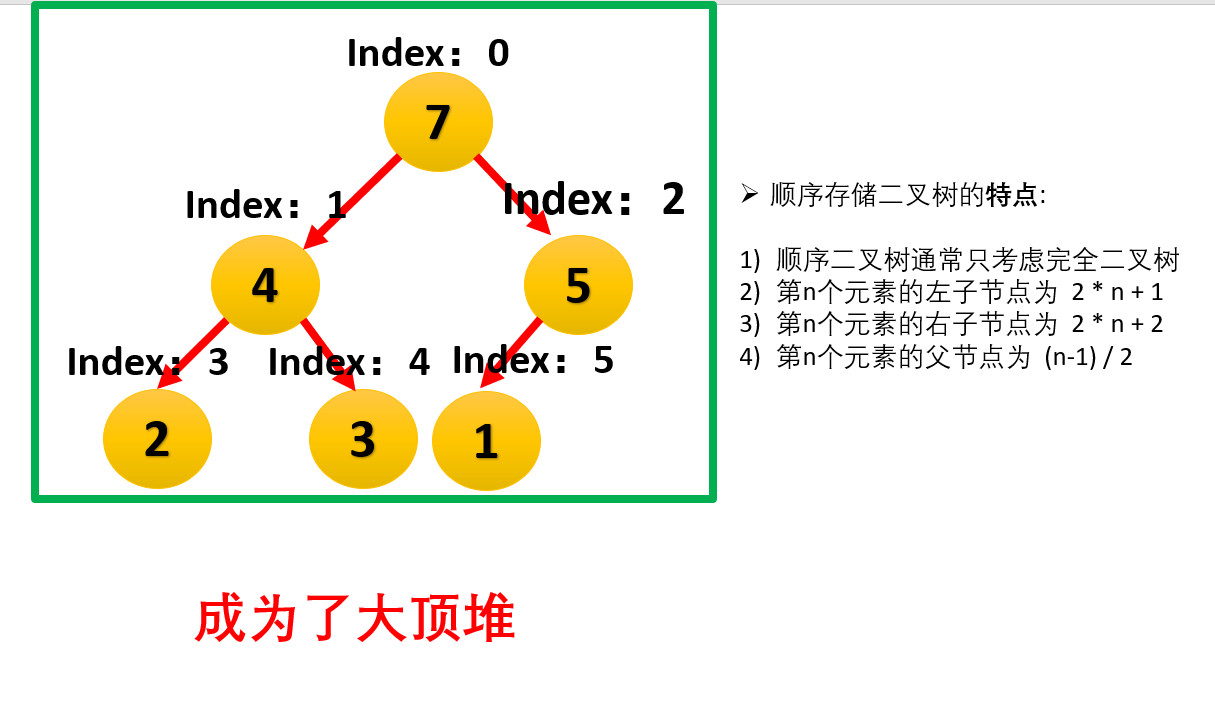
- Exchange the top element of the heap with the last element to maximize the last element. Then continue to adjust the heap, and then exchange the top element with the last element to get the second largest element. Such repeated exchange, reconstruction and exchange
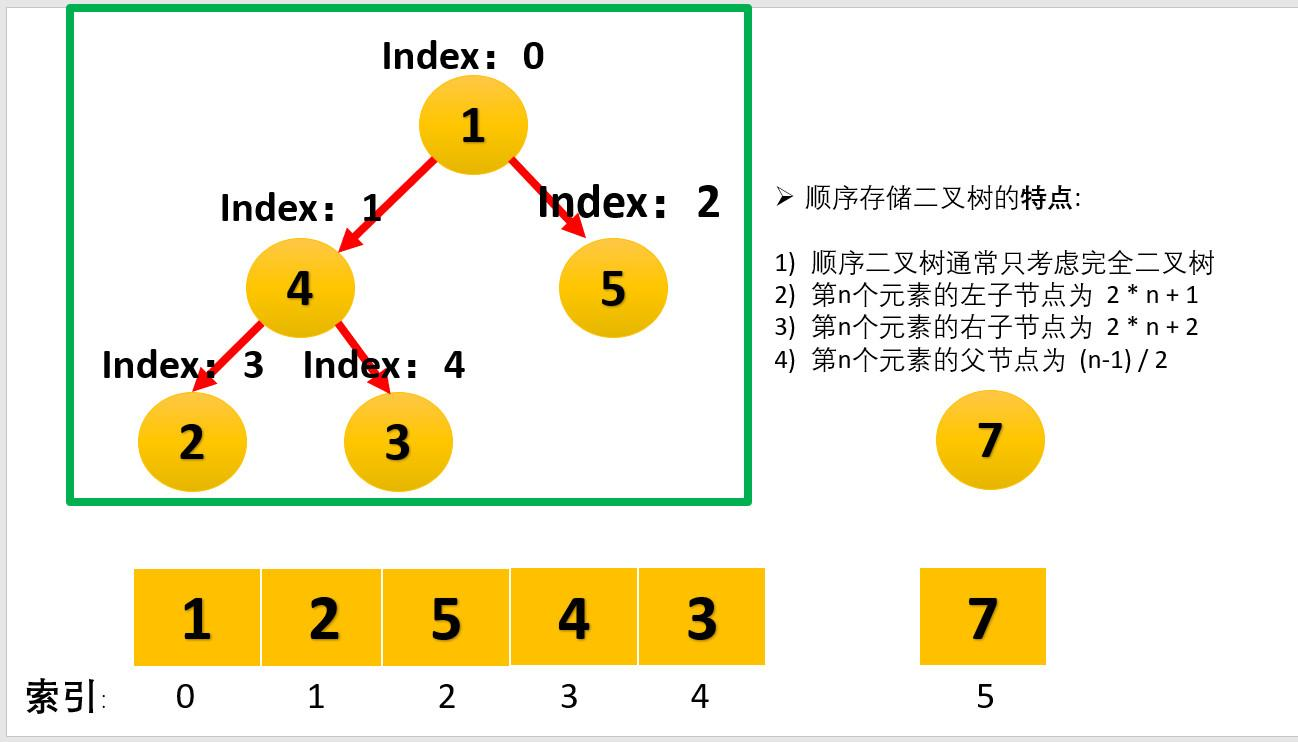
- Finally, heap sorting is realized
realization
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int data[] = { 8, 4, 20, 7, 3, 1, 25, 14, 17 };
heapSort(data);
System.out.println(Arrays.toString(data));
}
public static void maxHeap(int data[], int start, int end) {
int parent = start;
int son = parent * 2 + 1; // If the subscript starts from 0, add 1, and don't use 1
while (son < end) {
int temp = son;
// Compare the size of left and right nodes and parent nodes
if (son + 1 < end && data[son] < data[son + 1]) { // Indicates that the right node is larger than the left node
temp = son + 1; // You need to change the right node and the parent node
}
// temp indicates the one with the largest left and right nodes
if (data[parent] > data[temp])
return; // No exchange
else { // exchange
int t = data[parent];
data[parent] = data[temp];
data[temp] = t;
parent = temp; // Continue stacking
son = parent * 2 + 1;
}
}
return;
}
public static void heapSort(int data[]) {
int len = data.length;
for (int i = len / 2 - 1; i >= 0; i--) {
maxHeap(data, i, len);
}
for (int i = len - 1; i > 0; i--) {
int temp = data[0];
data[0] = data[i];
data[i] = temp;
maxHeap(data, 0, i);
}
}
}