Depth first search maze problem

Video learning link: https://www.bilibili.com/video/BV1pk4y1z76B
Depth first search: referred to as dfs, is a classic search algorithm.

Recursive review

We have studied recursion before. We have implemented some algorithms using recursion:

# 1. Recursive factorial
# n! = 1*2*3*4******n
def factorial(n):
	if (n ==1 ):
		return 1
	else:
		return n *factorial(n-1)
print(factorial(10))
# 2. Fiboracci sequence
# 1 1 2 3 5 8------
def fib(n):
	if (n==1||n==2):
		return 1
	else:
		return fib(n-1)+fib(n-2)

Deep first search is actually an exhaustive way, listing all feasible schemes and trying them until the solution of the problem is found.

The difference between depth first search and recursion is: depth first search is an algorithm that focuses on ideas; Recursion is an implementation method based on programming language. Depth first search can be realized by recursion, that is to say, recursion is the means that we use computer programming language to realize the algorithm of depth first search.

Next, we learn dfs through a practical problem - maze game

maze game

We use a two-dimensional character array to represent the maze drawn earlier:

S**
···
***T

The character S represents the starting point, the character T represents the ending point, the character * represents the wall, and the character · represents the flat ground. Each time, you can only move up, down, left and right adjacent positions. You can't go out of the map or through the wall. Each point can only pass once. You need programming to solve a walking method from the beginning to the end.

dfs is needed to solve the maze problem We try in four directions, up, down, left and right, one direction and one direction. If we can't reach the end along one direction, we have to return the same way and continue to try other directions until we get out of the maze. This is the most simple way to walk the maze. Although the efficiency may be relatively low, if the maze has a solution, it will be able to get out of the end.

The above-mentioned walking method corresponds to the dfs algorithm we want to talk about. First find the starting point s, and when you reach each point, try in the order of left, bottom, right and top (counterclockwise). Take each point as the starting point and continue to the next point in this order. If a point has been tried in four directions up, down, left and right, we will return to the point before this point. This step is called backtracking. Continue to try other directions. Until all points have tried up, down, left and right directions.

It's like walking this maze by yourself. You have to try to walk in one direction. If this road doesn't work, go back and try the next road. The idea of dfs is very similar to our intuitive idea. However, next we need to use programs to complete this process.

Maze Basic Edition

# 3 maze Basic Edition
# ranks
n , m = [int(i) for i in input("").split()]
# Maze initialization
maze = []
for i in range(0,n):
	list1 = list(input(""))
	maze.append(list1)
# Mark the maze
vis = []
for i in range(0,n):
	list1 = [0]*m
	vis.append(list1)


def dfs(x,y):
	# Return true if out of the maze
	if(maze[x][y]=="T"):
		return 1
	# Mark the position
	vis[x][y] = 1
	# Display path
	maze[x][y] ='m'
	# Upper left lower right
	# upper
	tx = x - 1 
	ty = y
	if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
		if (dfs(tx,ty)):
			return 1
	# Left
	tx = x 
	ty = y - 1
	if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
		if (dfs(tx,ty)):
			return 1
	# lower
	tx = x + 1
	ty = y 
	if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
		if (dfs(tx,ty)):
			return 1
	# right
	tx = x 
	ty = y + 1
	if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
		if (dfs(tx,ty)):
			return 1
	# Unmark when it cannot be found
	vis[x][y] = 0
	maze[x][y] ='.'
	return 0

# Start the maze
for i in range(0,n):
	for j in range(0,m):
		# Find starting point
		if maze[i][j] == 'S':
			x = i
			y = j
# Show the path if you can walk through it
if dfs(x,y):
	for i in range(0,n):
		print(maze[i])
# NO will be displayed if it cannot go through
else:
	print("NO!")

Test:

Maze compact

# 4 maze Lite
# ranks
n , m = [int(i) for i in input("").split()]
# Maze initialization
maze = []
for i in range(0,n):
	list1 = list(input(""))
	maze.append(list1)
# Mark the maze
vis = []
for i in range(0,n):
	list1 = [0]*m
	vis.append(list1)

# ---------Advanced modification part

# Save the direction as an array: top left bottom right
direction = [[-1,0],[0,-1],[1,0],[0,1]]

def dfs(x,y):
	# Return true if out of the maze
	if(maze[x][y]=="T"):
		return 1
	# Mark the position
	vis[x][y] = 1
	# Display path
	maze[x][y] ='m'

	# Upper left lower right
	for i in range(0,len(direction)):
		tx = x + direction[i][0]
		ty = y + direction[i][1]
		if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
			if (dfs(tx,ty)):
				return 1

	# Unmark when it cannot be found
	vis[x][y] = 0
	maze[x][y] ='.'
	return 0

# -------------Advanced modification part

# Start the maze
for i in range(0,n):
	for j in range(0,m):
		# Find starting point
		if maze[i][j] == 'S':
			x = i
			y = j
# Show the path if you can walk through it
if dfs(x,y):
	for i in range(0,n):
		print(maze[i])
# NO will be displayed if it cannot go through
else:
	print("NO!")
    
# The test results are the same

Maze Advanced Edition

(number of routes, route map and minimum steps of maze)

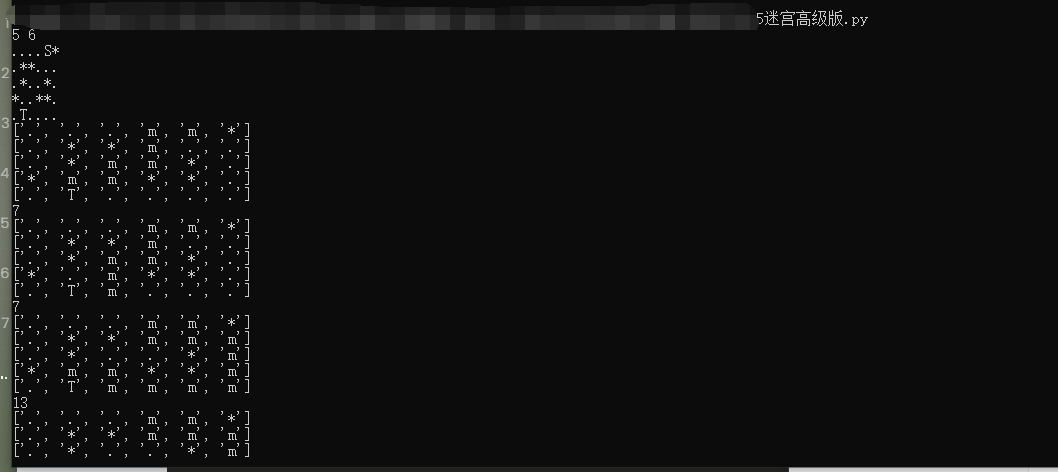
# 5 maze Advanced Edition
# ranks
n , m = [int(i) for i in input("").split()]
# Maze initialization
maze = []
for i in range(0,n):
	list1 = list(input(""))
	maze.append(list1)
# Mark the maze
vis = []
for i in range(0,n):
	list1 = [0]*m
	vis.append(list1)

# ------------------Higher order modification

# Save the direction as an array: top left bottom right
direction = [[-1,0],[0,-1],[1,0],[0,1]]
# Storage of route steps
dirstep = []

def dfs(x,y,step):
	# Return true if out of the maze
	if(maze[x][y]=="T"):
		# Output Roadmap
		for j in range(0,n):
			print(maze[j])
		# Output the number of steps of the route
		print(step)
		dirstep.append(step)
		return 1
	# Mark the position
	vis[x][y] = 1
	# Display path
	maze[x][y] ='m'

	# Upper left lower right
	for i in range(0,len(direction)):
		tx = x + direction[i][0]
		ty = y + direction[i][1]
		if tx >= 0 and tx < n and ty >= 0 and ty < m and maze[tx][ty] != '*' and vis[tx][ty] == 0 :
			dfs(tx,ty,step+1)

	# Unmark when it cannot be found
	vis[x][y] = 0
	maze[x][y] ='.'
	return 0

# Start the maze
for i in range(0,n):
	for j in range(0,m):
		# Find starting point
		if maze[i][j] == 'S':
			x = i
			y = j
# Call function
dfs(x,y,0)

print(dirstep)
# Minimum steps
print(min(dirstep))
# How many ways to walk
print(len(dirstep))

if len(dirstep) > 0:
	print("Yes")
else:
	print("NO")

# ------------------Higher order modification

Test:

Maze exercises

Title Requirements

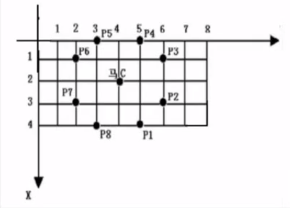
Chinese chess is broad and profound, among which the rules of horse are the most complex and the most difficult to control.
We all know that in chess, a horse goes "day". For example, for a horse in position (2, 4), the positions that can be reached by jumping one step are (0,3), (0, 5), (1,2), (1,6), (3,2), (3,6), (4,3), (4,5).

The garlic king is playing chess with the flower coconut sister. The garlic king is making a strategic layout. He needs to jump the horse in position (x, y) to position (x ', y') to achieve the purpose of deterrence.
However, the size of the chessboard is limited. The chessboard is a 10 x 9 grid. The coordinates of the upper left corner are (0,0) and the coordinates of the lower right corner are (9,8),
The horse can't go out of the chessboard, and there are pieces in some places, and the horse can't jump to the point where there are pieces.
Garlic Jun wants to know whether he can achieve his strategic goal without moving other pieces.

Input format
Enter a total of 10 lines, each with a string of length 9. Input represents this chessboard. We use "." Indicates an empty position,
Use '#' to indicate that there are pieces in this position, use'S' to indicate the initial position of the horse, and use'T 'to indicate the position where the horse needs to jump.
The input guarantees that there must be only one'S' and one'T '.

Output format
If the horse can jump from'S' to'T 'without moving other pieces, a line of "Yes" is output; otherwise, a line of "Yes" is output
Line "No"

Problem solving

# Build a maze
maze = []
for i in range(0,10):
	list1 = list(input(""))
	maze.append(list1)

# Create maze markers
vis = []
for i in range(0,10):
	list1 = [0]*9
	vis.append(list1)

direction = [[-2,-1],[-1,-2],[1,-2],[2,-1],[2,1],[1,2],[-1,2],[-2,1]]

def dfs(x,y):
	if maze[x][y] == 'T':
		return 1
	# Mark
	vis[x][y] = 1
	maze[x][y] = 'm'

	# Traverse the direction
	for i in range(0,len(direction)):
		tx = x + direction[i][0]
		ty = y + direction[i][1]
		if tx >= 0 and tx < 10 and ty >= 0 and ty < 9 and maze[tx][ty] != '#' and vis[tx][ty] == 0:
			if dfs(tx,ty):
				return 1


	# If not found, unmark
	vis[x][y] = 0
	maze[x][y] = '.'
	return 0

# Traverse the maze and find the starting point
for i in range(0,10):
	for j in range(0,9):
		if maze[i][j] == 'S':
			x = i
			y = j

if dfs(x,y):
	print('YES')
	for i in range(0,10):
		print(maze[i])
else:
	print('NO')