- Results fill in the blanks (full score 3 points)
- Results fill in the blanks (full score 5 points)
- Results fill in the blanks (full score 9 points)
- Fill in the blank with code (out of 11 points)
- Fill in the blank with code (Full Score 13 points)
- Results fill in the blanks (Full Score: 15 points)
- Results fill in the blanks (Full Score 19 points)
- Programming (Full Score: 21)
- Programming (out of 23 points)
- Programming (Full Score: 31 points)
Question 1: number of briquettes
There is a pile of coal balls, piled into a triangular pyramid. Specific:
One on the first floor,
Three on the second layer (arranged in a triangle),
6 on the third layer (arranged in a triangle),
10 on the fourth layer (arranged in a triangle),
....
If there are 100 floors, how many briquettes are there?
Please fill in the number indicating the total number of briquettes.
Note: what you submit should be an integer. Do not fill in any redundant content or explanatory text
Answer: 171700
public class Main {
public static void main(String[] args) {
int a=1,b=2,sum=1;
for (int i = 2; i <= 100; i++) {
sum += (a+b);
a+=b;
b++;
}
System.out.println(sum);
}
}
Question 2: birthday candles
A gentleman has held a birthday party every year since a certain year, and he has to blow out the same number of candles as his age every time.
Now he blows out 236 candles.
Excuse me, how old did he start his birthday party?
Please fill in the age of his birthday party.
Note: what you submit should be an integer. Do not fill in any redundant content or explanatory text.
Answer: 26
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
for(int i=1;i<50;i++) {
int sum=0;
for(int j=i;j<50;j++) {
sum+=j;
if(sum==236) {
System.out.println(i);
j=100; //Exit loop
i=100;
}else if(sum>236){
break;
}else {
continue;
}
}
}
}
}Question 3: building blocks
Xiao Ming likes building digital blocks recently,
There are 10 blocks in total, and each block has a number, 0 ~ 9.
Building block rules:
Each building block is placed on top of the other two building blocks, and the number must be smaller than the two building blocks below.
Finally, it is built into a 4-story pyramid, and all the building blocks must be used up.
Here are two qualified methods:
0
1 2
3 4 5
6 7 8 9
0
3 1
7 5 2
9 8 6 4
Please calculate the total number of such methods?
Please fill in a number indicating the total.
Note: what you submit should be an integer. Do not fill in any redundant content or explanatory text.
Answer: 978
import java.util.HashSet;
public class Main {
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
static HashSet<String> set = new HashSet<>();
static int[] a = new int[] {0,1,2,3,4,5,6,7,8,9};
static int ans=0;
static void dfs(int m) {
if(m>=10) {
if(a[0]>=a[1]||a[0]>=a[2])
return;
if(a[1]>=a[3]||a[1]>=a[3])
return;
if(a[2]>=a[4]||a[2]>=a[5])
return;
if(a[3]>=a[6]||a[3]>=a[7])
return;
if(a[4]>=a[7]||a[4]>=a[8])
return;
if(a[5]>=a[8]||a[5]>=a[9])
return;
String s="";
for(int i=0;i<10;i++) {
s+=a[i];
System.out.print(a[i]+" ");
}
System.out.println();
// if(!set.contains(s)) {
// set.add(s);
// ans++;
// }
ans++;
return;
}
for(int i=m;i<10;i++) {
swap(m,i);
dfs(m+1);
swap(m,i);
}
}
static void swap(int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}Question 4: divide into groups
Nine athletes participate in the competition and need to be divided into three groups for preliminary competition.
What are the grouping schemes?
We mark athletes as a, B, C I
The following procedure lists all grouping methods.
The normal output of this program is:
ABC DEF GHI
ABC DEG FHI
ABC DEH FGI
ABC DEI FGH
ABC DFG EHI
ABC DFH EGI
ABC DFI EGH
ABC DGH EFI
ABC DGI EFH
ABC DHI EFG
ABC EFG DHI
ABC EFH DGI
ABC EFI DGH
ABC EGH DFI
ABC EGI DFH
ABC EHI DFG
ABC FGH DEI
ABC FGI DEH
ABC FHI DEG
ABC GHI DEF
ABD CEF GHI
ABD CEG FHI
ABD CEH FGI
ABD CEI FGH
ABD CFG EHI
ABD CFH EGI
ABD CFI EGH
ABD CGH EFI
ABD CGI EFH
ABD CHI EFG
ABD EFG CHI
..... (omitted below, 560 lines in total)
public class Main {
public static String remain(int[] a) {
String s = "";
for (int i = 0; i < a.length; i++) {
if (a[i] == 0)
s += (char) (i + 'A');
}
return s;
}
public static void f(String s, int[] a) {
for (int i = 0; i < a.length; i++) {
if (a[i] == 1)
continue;
a[i] = 1;
for (int j = i + 1; j < a.length; j++) {
if (a[j] == 1)
continue;
a[j] = 1;
for (int k = j + 1; k < a.length; k++) {
if (a[k] == 1)
continue;
a[k] = 1;
System.out.println(); // Fill in the blanks
a[k] = 0;
}
a[j] = 0;
}
a[i] = 0;
}
}
public static void main(String[] args) {
int[] a = new int[9];
a[0] = 1;
for (int b = 1; b < a.length; b++) {
a[b] = 1;
for (int c = b + 1; c < a.length; c++) {
a[c] = 1;
String s = "A" + (char) (b + 'A') + (char) (c + 'A');
f(s, a);
a[c] = 0;
}
a[b] = 0;
}
}
}Question 5: draw lots
Planet X will send a five member observation mission to planet W.
Of which:
Country A can send up to four people.
Country B can send up to 2 people.
Country C can send up to 2 people.
....
So how many different combinations of countries will there be in the final observation mission to planet W?
The following procedure solves this problem.
Array a [] is the largest number of places that each country can send.
The program execution result is:
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
(omitted below, 101 lines in total)
public class A
{
public static void f(int[] a, int k, int n, String s)
{
if(k==a.length){
if(n==0) System.out.println(s);
return;
}
String s2 = s;
for(int i=0; i<=a[k]; i++){
_____________________________; //Fill in the blanks
s2 += (char)(k+'A');
}
}
public static void main(String[] args)
{
int[] a = {4,2,2,1,1,3};
f(a,0,5,"");
}
}answer: f(a,k+1,n-i,s2);
Question 6: winter vacation homework
Now the math problems in primary school are not so fun.
Look at this winter vacation assignment:
□ + □ = □
□ - □ = □
□ × □ = □
□ ÷ □ = □
(if it cannot be displayed, please refer to [figure 1.jpg])
Each box represents a number from 1 to 13, but cannot be repeated.
For example:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
And:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
Even if there are two solutions. (different schemes of addition, multiplication and commutative law)
How many options have you found?
Please fill in an integer representing the number of schemes.
Note: what you submit should be an integer. Do not fill in any redundant content or explanatory text
Answer: 64
public class Main {
public static void main(String[] args) {
dfs(0);
System.out.println(ans);
}
static int[] a = new int[] {1,2,3,4,5,6,7,8,9,10,11,12,13};
static int ans=0;
static void dfs(int m) {
if(m>=13) {//+ - * /
if(a[0]+a[1]==a[2] && a[3]-a[4]==a[5] && a[6]*a[7]==a[8] && a[9]/a[10]==a[11] && a[9]%a[10]==0) {
if(ans<10) {//11/2==5
System.out.println(a[0]+"+"+a[1]+"=="+a[2]);
System.out.println(a[3]+"-"+a[4]+"=="+a[5]);
System.out.println(a[6]+"*"+a[7]+"=="+a[8]);
System.out.println(a[9]+"/"+a[10]+"=="+a[11]);
System.out.println();
}
ans++;
}
return;
}
if(m>=3 && a[0]+a[1]!=a[2])//Pruning, 2 ^ 13 can't run out
return;
if(m>=6 && a[3]-a[4]!=a[5])//This can be cut or not. It ran out anyway
return;
for(int i=m;i<13;i++) {
swap(m,i);
dfs(m+1);
swap(m,i);
}
}
static void swap(int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}Question 7: cutting stamps
As shown in [figure 1.jpg], there are 12 stamps of the 12 Chinese zodiac animals connected together. Now you have to cut five of them. They must be connected. (only one corner is not connected)

For example, in [figure 2.jpg] and [figure 3.jpg], the part shown in pink is qualified cutting. Please calculate how many different cutting methods there are
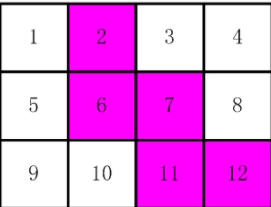
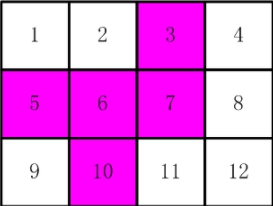
import java.util.Arrays;
import java.util.HashSet;
public class Main{
public static void main(String[] args) {
for(int i=1;i<=12;i++) {
for(int j=i+1;j<=12;j++) {
for(int k=j+1;k<=12;k++) {
for(int x=k+1;x<=12;x++) {
for(int y=x+1;y<=12;y++) {
vis[i]=vis[j]=vis[k]=vis[x]=vis[y]=true;
t=0;
dfs(i);
if(t==5)
ans++;
vis[i]=vis[j]=vis[k]=vis[x]=vis[y]=false;
}
}
}
}
}
System.out.println(ans);
}
// static char[] a = new char[] {'A','B','C','D','E','F','G','H','I','J','K','L'};
// static HashSet<String> set = new HashSet<>();
static boolean[] vis = new boolean[13];
static int ans = 0;
static int t=0;
static void dfs(int x) {
vis[x]=false;
t++;
if(x!=1 && x!=5 && x!=9 && vis[x-1])
dfs(x-1);
if(x!=4 && x!=8 && x!=12 && vis[x+1])
dfs(x+1);
if(x!=1 && x!=2 && x!=3 && x!=4 && vis[x-4])
dfs(x-4);
if(x!=9 && x!=10 && x!=11 && x!=12 && vis[x+4])
dfs(x+4);
}
}Question 8: game of taking the ball
Two people play the game of taking the ball.
There are n balls in total. Each person can take the ball in turn, and any number in the set {n1,n2,n3} can be taken each time.
If you cannot continue to take the ball, the game is over.
At this point, the party holding an odd number of balls wins.
If both are odd, it is a draw.
Assuming that both sides adopt the smartest approach,
Is the first person to take the ball sure to win?
Try programming to solve this problem.
Input format:
The first line contains three positive integers N1, N2 and N3, separated by spaces, indicating the number that can be taken each time (0 < N1, N2, N3 < 100)
The second line has five positive integers X1 x2 X5, separate spaces, indicating the initial number of balls in 5 rounds (0 < Xi < 1000)
Output format:
A line of five characters, separated by spaces. It indicates whether the person who takes the ball first in each game can win.
If you can win, you will output +,
Second, if there is a way to draw the opponent, output 0,
If it will lose anyway, it will be output-
For example, enter:
1 2 3
1 2 3 4 5
The program should output:
+ 0 + 0 -
For another example, enter:
1 4 5
10 11 12 13 15
The program should output:
0 - 0 + +
For another example, enter:
2 3 5
7 8 9 10 11
The program output should:
+ 0 0 0 0
Resource agreement:
Peak memory consumption (including virtual machine) < 256M
CPU consumption < 3000ms
Please output in strict accordance with the requirements, and do not print like "please input..." Superfluous content.
All code is placed in the same source file. After debugging, the copy is submitted to the source code.
Note: do not use package statements. Do not use jdk1 7 and above.
Note: the name of the Main class must be: Main, otherwise it will be treated as an invalid code
import java.util.Arrays;
import java.util.Scanner;
public class Main {
private static int[] n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = new int[3];
for (int i = 0; i < 3; i++) {
n[i] = sc.nextInt();
}
Arrays.sort(n);//sort
for (int i = 0; i < 5; i++) {
int num = sc.nextInt();
char res = f(num, 0, 0);
System.out.print(res + " ");
}
System.out.println();
}
static char[][][]cache = new char[1000][2][2];
/**
* The parameter represents the current situation faced by the receiver
* @param num Total number of balls
* @param me Number we hold -- > parity of our number
* @param you Number of opponents - parity of the number of opponents
* @return
*/
private static char f(int num, int me, int you) {
if (num<n[0])//Not enough
{
if ((me&1)==1&&(you&1)==0)return '+';
else if ((me&1)==0&&(you&1)==1)return '-';
else return '0';
}
if (cache[num][me][you]!='\0')return cache[num][me][you];
boolean ping = false;
for (int i = 0; i < 3; i++) {
if (num >= n[i]) {
char res = f(num - n[i], you, (n[i]&1)==0?me:(1-me));//Note here that the parity of me and you is passed
if (res == '-')
{
cache[num][me][you]='+';
return '+';
}
if (res == '0')
ping = true;
}
}
//If you can go to this line, it means that there is no opponent losing, so is there a flat situation
if (ping)
{
cache[num][me][you]='0';
return '0';
}
else
{
cache[num][me][you]='-';
return '-';
}
}
}Question 9: exchanging bottles
There are N bottles, numbered 1 ~ N, on the shelf.
For example, there are five bottles:
2 1 3 5 4
It is required to pick up 2 bottles at a time and exchange their positions.
After several times, the serial number of the bottle is:
1 2 3 4 5
For such a simple case, it is obvious that it can be reset by switching at least twice.
What if there are more bottles? You can solve it by programming.
The input format is two lines:
The first line: a positive integer N (N < 10000), indicating the number of bottles
The second line: N positive integers, separated by spaces, indicating the current arrangement of bottles.
The output data is a positive integer in a row, indicating how many times to exchange at least before sorting can be completed.
For example, enter:
5
3 1 2 5 4
The program should output:
3
For another example, enter:
5
5 4 3 2 1
The program should output:
2
Resource agreement:
Peak memory consumption (including virtual machine) < 256M
CPU consumption < 1000ms
Please output in strict accordance with the requirements, and do not print like "please input..." Superfluous content.
All code is placed in the same source file. After debugging, the copy is submitted to the source code.
Note: do not use package statements. Do not use jdk1 7 and above.
Note: the name of the Main class must be: Main, otherwise it will be treated as an invalid code
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n+1];
for(int i=1;i<=n;i++)
a[i] = in.nextInt();
int ans = 0;
for(int i=1;i<=n;i++)
if(a[i]!=i)
for(int j=i+1;j<=n;j++) {
if(a[j]==i) {
a[j]=a[i];
a[i]=a[i];
ans++;
break;
}
}
System.out.println(ans);
}
}Question 10: compression transformation
Xiao Ming is studying compression algorithms recently.
He knows that if the value can be made very small during compression, a higher compression ratio can be obtained through entropy coding.
However, making the value small is a challenge.
Recently, Xiao Ming needs to compress some sequences of positive integers. The characteristic of these sequences is that the numbers appearing later are likely to be those that have just appeared. For this special sequence, Xiao Ming is going to make a transformation to the sequence to reduce the value of the number.
The transformation process is as follows:
Enumerating the sequence from left to right, each enumerating a number. If the number has not appeared, just convert the number into its opposite number. If the number has appeared, see that several numbers appear after the last occurrence in the original sequence (and in front of the current number). Replace the original number with this kind of number.
For example, the sequence (a1, a2, a3, a4, a5)=(1, 2, 2, 1, 2) in the transformation process is:
a1: 1 does not appear, so a1 becomes - 1;
a2: 2 does not appear, so a2 becomes - 2;
a3: 2 has appeared. The last time is a2 of the original sequence. There are 0 numbers after a2 and before a3, so a3 becomes 0;
a4: 1 has appeared. The last time is a1 of the original sequence. There is a number after a1 and before a4, so a4 becomes 1;
a5: 2 has appeared. The last time is a3 of the original sequence. There is a number after a3 and before a5, so a5 becomes 1.
Now, given the original sequence, what is the sequence transformed according to this transformation rule.
Input format:
The first line of input contains an integer n, which represents the length of the sequence.
The second line contains n positive integers representing the input sequence.
Output format:
Output a line containing n numbers, representing the transformed sequence.
For example, enter:
5
1 2 2 1 2
The program output should:
-1 -2 0 1 1
For another example, enter:
12
1 1 2 3 2 3 1 2 2 2 3 1
The program output should:
-1 0 -2 -3 1 1 2 2 0 0 2 2
Data scale and agreement
For 30% data, n < = 1000;
For 50% data, n < = 30000;
For 100% data, 1 < = n < = 100000, 1 < = AI < = 10 ^ 9
Resource agreement:
Peak memory consumption (including virtual machine) < 256M
CPU consumption < 3000ms
Please output in strict accordance with the requirements, and do not print like "please input..." Superfluous content.
All code is placed in the same source file. After debugging, the copy is submitted to the source code.
Note: do not use package statements. Do not use jdk1 7 and above.
Note: the name of the Main class must be: Main, otherwise it will be treated as an invalid code
import java.util.HashSet;
import java.util.Scanner;
public class Main {
static HashSet<Integer> set = new HashSet<>();
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n+1];
int[] b = new int[n+1];
int[] pre = new int[n+1];
for(int i=1;i<=n;i++) {
a[i] = in.nextInt();
int j=i-1;
while(j>0 && a[j]!=a[i])
j--;
pre[i] = j;
}
for(int i=1;i<=n;i++) {
if(pre[i]==0)
b[i] = -a[i];
else {
set.clear();
for(int j=pre[i]+1;j<i;j++)
set.add(a[j]);
b[i] = set.size();
}
}
for(int i=1;i<=n;i++)
if(i!=n)
System.out.print(b[i]+" ");
else
System.out.println(b[i]);
}
}