WHAT?

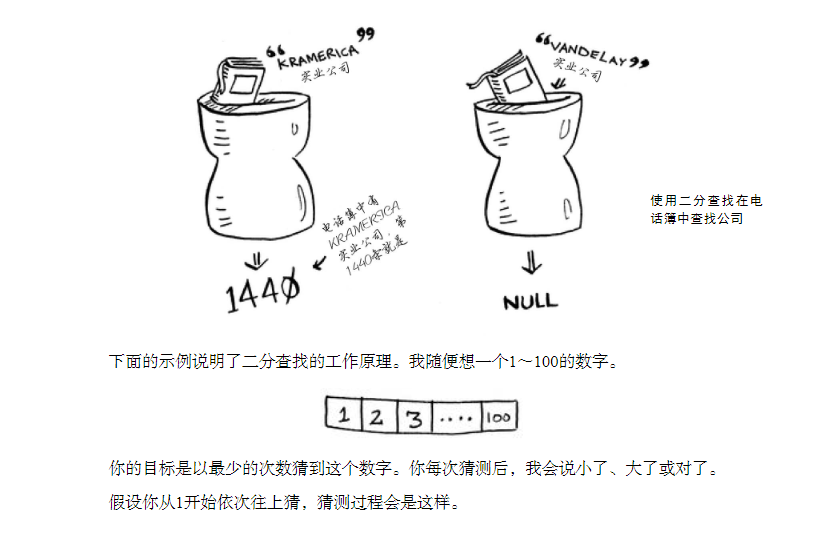
Suppose you want to find a person whose name starts with K in the phone book, (who still uses the phone book now!) You can turn the page from the beginning until you enter the part starting with K. But you probably don't do that, but start in the middle, because you know the name starting with K is in the middle of the phone book.

Suppose you want to find a word starting with O in the dictionary, you will also start near the middle. Now suppose you log in to Facebook. When you do this, Facebook must verify that you have an account on its website, so it must look up your user name in its database.

If your user name is karlmageddon, Facebook can start with the part starting with A, but it is more logical to start from the middle.

This is a search problem. In all the above cases, the same algorithm can be used to solve the problem. This algorithm is binary search.  

Binary search is an algorithm whose input is an ordered list of elements. If the element to be searched is included in the list, binary search returns its position; Otherwise, null is returned.

 

WHY?

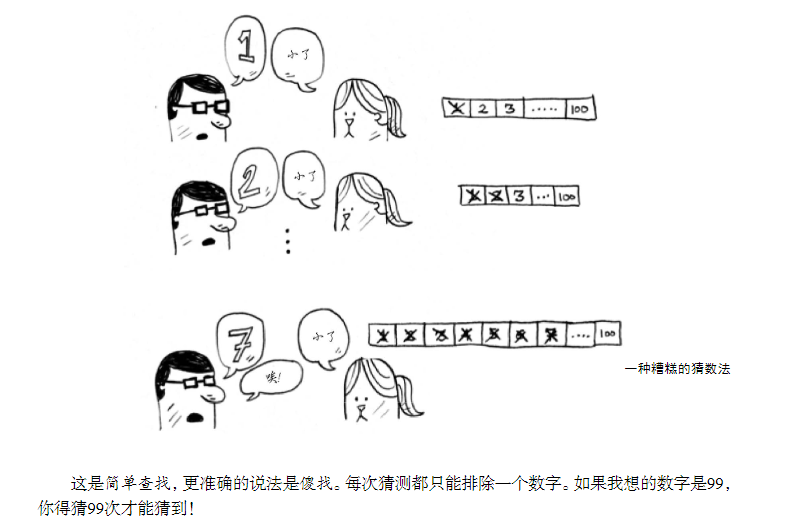
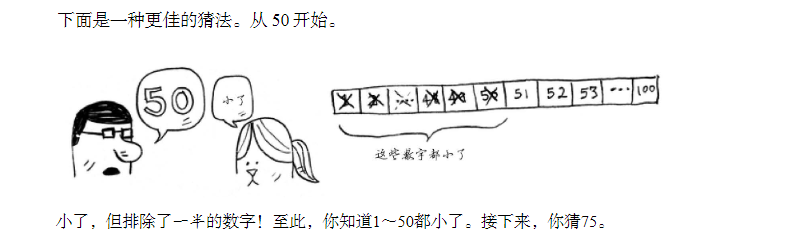
Do you think it's so troublesome? It's really annoying. (it affects my efficiency of paddling at work). You can do more methods in the same time. My little brother / sister knows a wave

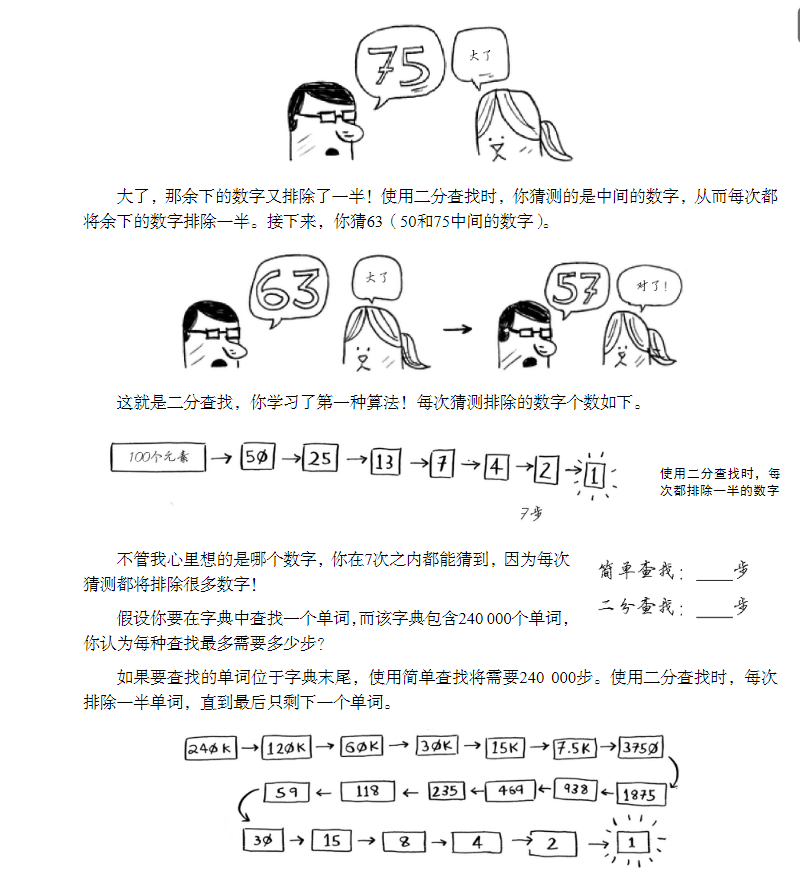
Therefore, using binary search only takes 18 steps - much less! Generally speaking, for a list containing n elements, a binary search requires up to log2n steps, while a simple search requires up to N steps.

(knocking on the blackboard) here comes the key knowledge. Remember it, little book

HOW？

1. Suppose there is an ordered list of 128 names. You need to use binary search to find a name in it. How many steps do you need to find at most?

2. After doubling the length of the above list, how many steps are required at most?

We focus on these two issues for logical implementation

<?php

$arr = [];
$lenght = 128;
$value = 127;
for ($i = 1; $i <= $lenght; $i++) {
    $arr[] = $i;
}

$res = BinarySearch::index($arr, $value);

echo $res;

class BinarySearch {
    public static function index(array $list, int $value) {
        //Calculation times
        $number = 0;

        $lowIndex = 0;
        $hightIndex = count($list) - 1;

        while($lowIndex <= $hightIndex) {
            $number++;
            $contentIndex = intval(($lowIndex + $hightIndex)/ 2);

            echo "[log] The first $number Times, minimum subscript $lowIndex ，Maximum subscript $hightIndex ，Find middle subscript($lowIndex + $hightIndex) / 2 = $contentIndex\n";

            if($list[$contentIndex] == $value) {
                echo "[log] eureka!\n";
                return sprintf("Pass section%d Search, found%d,The element subscript is%s\n", $number, $value, $contentIndex);
            } elseif($list[$contentIndex] < $value) {
                echo "[log] Subscript $contentIndex The value of is " . $list[$contentIndex] . " ,  " . $list[$contentIndex] . " than $value Small (subscript can be discarded) $contentIndex Value judgment of, i.e. minimum subscript = $contentIndex + 1)\n";
                $lowIndex = $contentIndex + 1;
            } else {
                echo "[log] Subscript $contentIndex The value of is " . $list[$contentIndex] . " ， " . $list[$contentIndex] . " than $value Large (subscript can be discarded) $contentIndex Value judgment of, i.e. maximum subscript = $contentIndex - 1)\n";
                $hightIndex = $contentIndex - 1;
            }
        }
        
        return "[log] Can't find $value\n";
    }
}
?>

What's the logic of fear after reading it

1. Why not use for instead of while

2. Subscript + 1 or - 1

3. For curious babies who want to know the answer, please ask questions in the comment area

 

Output results

[log] The first time, the minimum subscript is 0, the maximum subscript is 127, and the middle subscript is found(0 + 127) / 2 = 63
[log] The value with subscript 63 is 64 ,  64 Smaller than 127 (the value judgment of subscript 63 can be abandoned, i.e. the minimum subscript) = 63 + 1)
[log] The second time, the minimum subscript 64, the maximum subscript 127, find the middle subscript(64 + 127) / 2 = 95
[log] The value with subscript 95 is 96 ,  96 Smaller than 127 (the value judgment of subscript 95 can be abandoned, i.e. the minimum subscript) = 95 + 1)
[log] The third time, the minimum subscript 96, the maximum subscript 127, find the middle subscript(96 + 127) / 2 = 111
[log] The value with subscript 111 is 112 ,  112 Smaller than 127 (the value judgment of subscript 111, i.e. the minimum subscript, can be abandoned) = 111 + 1)
[log] The fourth time, the minimum subscript 112, the maximum subscript 127, find the middle subscript(112 + 127) / 2 = 119
[log] The value with subscript 119 is 120 ,  120 Smaller than 127 (the value judgment of subscript 119 can be abandoned, i.e. the minimum subscript) = 119 + 1)
[log] The fifth time, the minimum subscript 120, the maximum subscript 127, find the middle subscript(120 + 127) / 2 = 123
[log] The value with subscript 123 is 124 ,  124 Smaller than 127 (the value judgment of subscript 123 can be abandoned, i.e. the minimum subscript) = 123 + 1)
[log] The sixth time, the minimum subscript 124, the maximum subscript 127, find the middle subscript(124 + 127) / 2 = 125
[log] The value with subscript 125 is 126 ,  126 Smaller than 127 (the value judgment of subscript 125 can be abandoned, i.e. the minimum subscript) = 125 + 1)
[log] The 7th time, the minimum subscript 126, the maximum subscript 127, find the middle subscript(126 + 127) / 2 = 126
[log] eureka!
Through the 7th search, 127 were found,The element subscript is 126

Let's find out what the result is when we can't find the value in this range!

Case 1: find the data exceeding the maximum value. Here I use 200

[log] The first time, the minimum subscript is 0, the maximum subscript is 127, and the middle subscript is found(0 + 127) / 2 = 63
[log] The value with subscript 63 is 64 ,  64 Smaller than 200 (the value judgment of subscript 63, i.e. the minimum subscript, can be abandoned) = 63 + 1)
[log] The second time, the minimum subscript 64, the maximum subscript 127, find the middle subscript(64 + 127) / 2 = 95
[log] The value with subscript 95 is 96 ,  96 Smaller than 200 (the value judgment of subscript 95 can be abandoned, i.e. the minimum subscript) = 95 + 1)
[log] The third time, the minimum subscript 96, the maximum subscript 127, find the middle subscript(96 + 127) / 2 = 111
[log] The value with subscript 111 is 112 ,  112 Smaller than 200 (the value judgment of subscript 111, i.e. the minimum subscript, can be abandoned) = 111 + 1)
[log] The fourth time, the minimum subscript 112, the maximum subscript 127, find the middle subscript(112 + 127) / 2 = 119
[log] The value with subscript 119 is 120 ,  120 Smaller than 200 (the value judgment of subscript 119 can be abandoned, that is, the minimum subscript) = 119 + 1)
[log] The fifth time, the minimum subscript 120, the maximum subscript 127, find the middle subscript(120 + 127) / 2 = 123
[log] The value with subscript 123 is 124 ,  124 Smaller than 200 (the value judgment of subscript 123 can be abandoned, i.e. the minimum subscript) = 123 + 1)
[log] The sixth time, the minimum subscript 124, the maximum subscript 127, find the middle subscript(124 + 127) / 2 = 125
[log] The value with subscript 125 is 126 ,  126 Smaller than 200 (the value judgment of subscript 125 can be abandoned, that is, the minimum subscript = 125 + 1)
[log] The 7th time, the minimum subscript 126, the maximum subscript 127, find the middle subscript(126 + 127) / 2 = 126
[log] The value with subscript 126 is 127 ,  127 Smaller than 200 (the value judgment of subscript 126 can be abandoned, that is, the minimum subscript = 126 + 1)
[log] The 8th time, the minimum subscript 127, the maximum subscript 127, find the middle subscript(127 + 127) / 2 = 127
[log] The value with a subscript of 127 is 128 ,  128 Smaller than 200 (the value judgment of subscript 127 can be abandoned, i.e. the minimum subscript) = 127 + 1)
[log] I didn't find 200

Case 2: I can't find data that exceeds the minimum value. Here I use - 10

[log] The first time, the minimum subscript is 0, the maximum subscript is 127, and the middle subscript is found(0 + 127) / 2 = 63
[log] The value with subscript 63 is 64, 64 ratio -10 Large (the value judgment of subscript 63 can be abandoned, that is, the maximum subscript = 63 - 1)
[log] The second time, the minimum subscript 0, the maximum subscript 62, find the middle subscript(0 + 62) / 2 = 31
[log] The value with subscript 31 is 32, 32 to 32 -10 Large (the value judgment of subscript 31 can be abandoned, that is, the maximum subscript = 31 - 1)
[log] The third time, the minimum subscript is 0, the maximum subscript is 30, and the middle subscript is found(0 + 30) / 2 = 15
[log] The value with subscript 15 is 16, 16 to 16 -10 Large (the value judgment of subscript 15 can be abandoned, that is, the maximum subscript = 15 - 1)
[log] The 4th time, the minimum subscript 0, the maximum subscript 14, find the middle subscript(0 + 14) / 2 = 7
[log] The value with subscript 7 is 8 to 8 -10 Large (the value judgment of subscript 7 can be abandoned, that is, the maximum subscript = 7 - 1)
[log] The 5th time, the minimum subscript 0, the maximum subscript 6, find the middle subscript(0 + 6) / 2 = 3
[log] The value with subscript 3 is 4 to 4 -10 Large (the value judgment of subscript 3 can be abandoned, i.e. the maximum subscript) = 3 - 1)
[log] The 6th time, the minimum subscript 0, the maximum subscript 2, find the middle subscript(0 + 2) / 2 = 1
[log] The value with subscript 1 is 2 to 2 -10 Large (the value judgment of subscript 1 can be abandoned, i.e. the maximum subscript) = 1 - 1)
[log] The 7th time, the minimum subscript 0, the maximum subscript 0, find the middle subscript(0 + 0) / 2 = 0
[log] The value with subscript 0 is 1 to 1 -10 Large (the value judgment of subscript 0 can be abandoned, that is, the maximum subscript = 0 - 1)
[log] Can't find -10